Theoreme d'Ascoli

Theoreme d'Ascoli: Théorème d'Ascoli

En analyse fonctionnelle, le théorème d'Ascoli est un puissant résultat caractérisant les parties relativement compactes de l'espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se généralise sans difficulté au cas où l'espace de départ est seulement localement compact.

Ce théorème est connu pour son nombre considérable d'applications (complétude de certains espaces fonctionnels, compacité de certains opérateurs, dépendance en les conditions initiales dans les équations différentielles ...).

Sommaire

1 Énoncé

2 Démonstration

2.1 Condition nécessaire

2.2 Condition suffisante

2.3 Condition suffisante, seconde preuve

3 Opérateurs à noyau

4 Références

Énoncé

Dans un espace vectoriel normé de dimension finie, les parties compactes sont exactement les parties fermées et bornées. Dans un espace vectoriel topologique séparé, les parties relativement compactes restent bornées ; mais la réciproque est fausse. Le théorème d'Ascoli traite du cas de l'espace des fonctions continues :

Soient 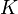$K\;$ un espace compact et 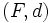$(F,d)\;$ un espace métrique. L'espace 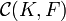$\mathcal{C}(K,F)$ des fonctions continues de K dans F, muni de la distance uniforme, est un espace métrique.

Une partie A de 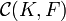$\mathcal{C}(K,F)$ est relativement compacte si et seulement si les deux conditions suivantes sont respectées :

A est équicontinue, i.e pour tout 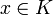$x \in K$ , on a

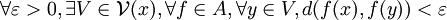
$\forall \varepsilon > 0, \exists V\in\mathcal V(x), \forall f \in A, \forall y \in V, d(f(x),f(y)) < \varepsilon$

Pour tout 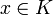$x \in K$ , l'ensemble 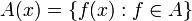$A(x) = \{f(x) : f \in A\}$ est relativement compact.

Un ensemble de fonctions r-lipschitziennes est un exemple d'ensemble équicontinu.

Il existe de nombreuses variantes du théorème d'Ascoli.

Démonstration

Le théorème d'Ascoli établit une équivalence. Les deux implications sont démontrées séparément. Les notations sont celles de l'énoncé ci-dessus.

Condition nécessaire

Notons B l'adhérence de A dans 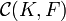$\mathcal{C}(K,F)$ . Supposons que B soit compact et fixons $x\in K$ .

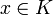Pour montrer que A(x) est relativement compact dans F, il suffit de remarquer qu'il est inclus dans B(x) qui est compact, comme image du compact B par l'application continue de C(K,F) dans F qui à f associe f(x).

Montrons maintenant l'équicontinuité de B au point x (qui entraînera celle de A). Soit $\varepsilon$ un réel >0.

Par précompacité de B, il existe un nombre fini d'éléments 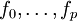$f_0,\ldots,f_{p}$ dans B tels que toute fonction f dans B se trouve à une distance au plus $ε$ de l'un des $f j$ .

Par continuité en x de 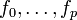$f_0,\ldots,f_p$ , il existe un voisinage V de x tel que
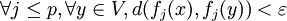$\forall j\leq p,\forall y\in V, d(f_j(x),f_j(y))<\varepsilon$ .
Pour toute fonction f dans B et tout point y dans V, l'inégalité triangulaire donne :
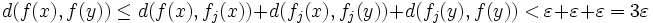$d(f(x),f(y))\le d(f(x),f_j(x))+d(f_j(x),f_j(y))+d(f_j(y),f(y))<\varepsilon+\varepsilon+\varepsilon=3\varepsilon$ ,
d'où l'équicontinuité de B.

Condition suffisante

La réciproque est le sens le plus souvent utilisé et demande plus d'attention. On souhaite démontrer qu'une partie équicontinue A de C(K,F) telle que A(x) soit relativement compacte pour tout x, est incluse dans un compact de C(K,F).

Notons C l'adhérence de A dans l'espace $F K$ des applications de K dans F muni de la topologie de la convergence simple (autrement dit, $F K$ est muni de la topologie produit). D'après les propriétés de l'équicontinuité, C est encore équicontinu, et les deux topologies sur C induites par son inclusion dans C(K,F) et dans $F K$ coïncident. Il suffit donc de prouver que C est un compact de $F K$ .

Introduisons le sous-espace 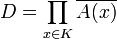$D=\prod_{x\in K}\overline {A(x)}$ de $F K$ . D'après le théorème de Tychonov, D est compact, or C est un fermé de D, ce qui conclut.

Condition suffisante, seconde preuve

Une alternative à l'utilisation du théorème de Tychonov est de prouver élémentairement que l'adhérence B de A dans C(K,F) est précompacte et complète (donc compacte), de la façon suivante.

Montrons d'abord que A est précompact (donc B aussi). Soit $ε > 0$ , montrons que A est recouvert par une famille finie d'ensembles $C j$ de diamètres 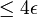$\leq 4\epsilon$ . Pour tout 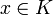$x\in K$ il existe (par équicontinuité de A) un voisinage ouvert $O x$ de $x$ tel que
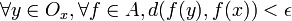$\forall y\in O_x,\forall f\in A,d(f(y),f(x))<\epsilon$ .
Par compacité de K, il existe alors une partie finie 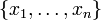$\{x_1,\ldots,x_n\}$ de K telle que les ouverts correspondants 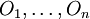$O_1,\ldots,O_n$ recouvrent K.

Posons 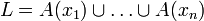$L=A(x_1)\cup\ldots\cup A(x_n)$ : L est relativement compact dans F donc il existe une partie finie J de F telle que les boules $B (j,ε)$ pour 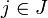$j\in J$ recouvrent L.

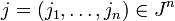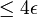Notons enfin, pour tout $j=(j_1,\ldots,j_n)\in J^n$ , l'ensemble (de diamètre $\leq 4\epsilon$ )
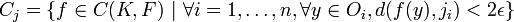$C_j=\{f\in C(K,F)\ |\ \forall i=1,\ldots,n,\forall y\in O_i,d(f(y),j_i)<2\epsilon\}$ .
Il reste à prouver que les $C j$ recouvrent A. Soit 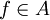$f\in A$ , comme les $f (x i)$ appartiennent à L, il existe 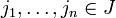$j_1,\ldots,j_n\in J$ tels que 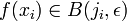$f(x_i)\in B(j_i,\epsilon)$ , ce qui implique 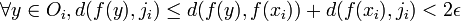$\forall y\in O_i, d(f(y),j_i)\leq d(f(y),f(x_i))+d(f(x_i),j_i)<2\epsilon$ , si bien que $f$ appartient à $C j$ .

Montrons ensuite que B est complet. Il suffit pour cela de prouver que toute suite de Cauchy d'éléments $f n$ de A converge dans C(K,F). Pour tout point x de K, la suite $(f n (x))$ est de Cauchy et à valeurs dans A(x), dont l'adhérence dans F est compacte donc complète, donc cette suite admet dans F une limite, f(x). Par équicontinuité, la convergence simple de $(f n)$ vers $f$ est uniforme sur le compact K.

Opérateurs à noyau

Article détaillé : opérateur à noyau.

Références

Georges Skandalis, Topologie et analyse 3e année, Édition Dunod, Collection Sciences Sup, 2001

Claude Wagschal, Topologie et analyse fonctionnelle, Édition Hermann, Collection Méthodes, 1995

Théorèmes de l'analyse fonctionnelle

Théorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram

modifier

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me d%27Ascoli ».

Catégories : Compacité | Analyse fonctionnelle | Théorème de mathématiques

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme d'Ascoli de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorème d'Ascoli — En analyse fonctionnelle, le théorème d Ascoli, ou théorème d Arzelà Ascoli, démontré par les mathématiciens italiens Giulio Ascoli et Cesare Arzelà (en), caractérise les parties relativement compactes de l espace des fonctions continues d… … Wikipédia en Français
Théorème d'Arzelà-Ascoli — Théorème d Ascoli En analyse fonctionnelle, le théorème d Ascoli est un puissant résultat caractérisant les parties relativement compactes de l espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se … Wikipédia en Français
Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… … Wikipédia en Français
Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… … Wikipédia en Français
Théorème de projection orthogonale sur un convexe — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Theoreme de Banach-Schauder — Théorème de Banach Schauder En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces… … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de banach-schauder — En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces vectoriels normés complets est … Wikipédia en Français
Théorème de l'application ouverte — Théorème de Banach Schauder En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts