- Theoreme de Krein-Milman
-
Théorème de Krein-Milman
Le théorème de Krein-Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par Hermann Minkowski en dimension finie (et souvent improprement dénommé lui-même « Théorème de Krein-Milman »).
Une forme particulièrement simplifiée du théorème s'énonce : tout polygone convexe est l'enveloppe convexe de l'ensemble de ses sommets. Cela est vrai aussi d'un polytope convexe.
Sommaire
La notion de « point extrémal »
Les points extrémaux sont ceux représentés en rouge
Soit C un convexe et c un point de C. On dit que c est un point extrémal de C lorsque
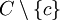est encore convexe. Cela équivaut à dire que, avec 
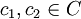, l'égalité 
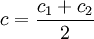implique c1 = c2 = c.L'énoncé en dimension finie
Théorème — Tout convexe compact d'un espace affine de dimension finie est enveloppe convexe de l'ensemble de ses points extrémaux.
La démonstration n'est pas très longue, l'outil essentiel étant le théorème d'existence d'un hyperplan d'appui en tout point de la frontière d'un convexe.
DémonstrationLa démonstration est une récurrence sur la dimension du convexe. Le résultat est évident pour un singleton ; supposons désormais le résultat vrai pour tous les convexes de dimension strictement inférieure à un entier fixé k, et soit C un convexe de dimension k.
Quitte à remplacer l'espace ambiant par l'enveloppe affine de C, on peut supposer que c'est un espace affine dont la dimension est également k.
Prenons maintenant un point m de C et montrons qu'il est dans l'enveloppe convexe des points extrémaux. Pour ce faire, on trace une droite D passant par m. L'ensemble
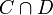est alors un convexe de D, compact par l'hypothèse de compacité faite sur C. Il est donc de la forme [a,b], où ![m\in [a,b]](/pictures/frwiki/57/9e6aaa2e15c536a74a51596181e6ffb8.png)
.Maintenant a comme b sont adhérents au complémentaire de C, ce sont donc des points frontières de ce convexe. Il existe donc des hyperplans d'appui Ha et Hb en ces points. Introduisons les convexes
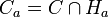et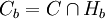 
.On remarque alors que tout point extrémal de Ca (rep. Cb) est encore un point extrémal de C. Soit en effet c un tel point extrémal de Ca, puis x et y deux points de
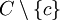. Si l'un au moins des deux points x et y n'est pas dans Ha, vu le caractère séparant de cet hyperplan, tout le segment ouvert ]x,y[ reste dans un seul demi-espace ouvert délimité par Ha et évite donc c ; si x et y sont tous les deux sur Ha, c'est la convexité de 
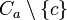qui assure que [x,y] évite c. Dans tous les cas le segment [x,y] est donc bien tout entier dans 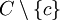et c est donc extrémal dans C.Par ailleurs, comme Ha et Hb sont de dimension k − 1, les deux convexes Ca et Cb sont de dimension strictement inférieure à k. On peut donc leur appliquer l'hypothèse de récurrence. Ceci montre que a (resp. b) est combinaison linéaire de points extrémaux de Ca (resp. Cb), donc de points extrémaux de C. Tant a que b appartient donc à l'enveloppe convexe de ces points extrémaux, puis à son tour m puisqu'il est sur le segment [a,b].
La généralisation en dimension infinie
Théorème — Tout convexe compact d'un espace localement convexe séparé est l'adhérence de l'enveloppe convexe de l'ensemble de ses points extrémaux.
Références
- Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of convex analysis, coll. « Grundlehren Text Editions », Springer, 2001 (ISBN 3540422056), p. 41-42, 57 et 246.
Bibliographie
- M. Krein, D. Milman (1940) On the extreme points of regularly convex sets, Studia Mathematica 9 133-138.
Portail des mathématiques
Catégories : Géométrie convexe | Théorème de mathématiques
Wikimedia Foundation. 2010.
