Application sous-lineaire

Regardez d'autres dictionnaires:

• Application sous-linéaire — Soit V un espace vectoriel sur . On dit qu une application 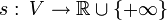est sous linéaire lorsque : (1) Pour tous vecteurs x et y de V, 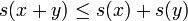(on dit que s est sous additive) (2) Pour tout vecteur x …   Wikipédia en Français

• Application Multilinéaire — En algèbre linéaire, une application multilinéaire est une application à plusieurs variables vectorielles qui est linéaire en chaque variable. Quelques exemples classiques : Le produit scalaire est une fonction bilinéaire symétrique à deux… …   Wikipédia en Français

• Application multilineaire — Application multilinéaire En algèbre linéaire, une application multilinéaire est une application à plusieurs variables vectorielles qui est linéaire en chaque variable. Quelques exemples classiques : Le produit scalaire est une fonction… …   Wikipédia en Français

• linéaire — [ lineɛr ] adj. et n. m. • XVe; lat. linearis, de linea → ligne 1 ♦ Qui a rapport aux lignes, se traduit par des lignes. Mesure linéaire : mesure de longueur. Dessin linéaire, où le trait seul est utilisé (cf. Au trait). Perspective linéaire… …   Encyclopédie Universelle

• Sous-espace supplementaire — Sous espace supplémentaire En mathématiques, un sous espace supplémentaire est un sous espace vectoriel défini par rapport à un autre sous espace qui, de manière intuitive (ne pas confondre avec la notion de complémentaire), sépare l espace en… …   Wikipédia en Français

• Sous-espaces supplémentaires — Sous espace supplémentaire En mathématiques, un sous espace supplémentaire est un sous espace vectoriel défini par rapport à un autre sous espace qui, de manière intuitive (ne pas confondre avec la notion de complémentaire), sépare l espace en… …   Wikipédia en Français

• LINÉAIRE ET MULTILINÉAIRE (ALGÈBRE) — LINЙAIRE ET MULTILINЙAIRE (ALGИBRE) L’algèbre linéaire sur un corps commutatif, telle qu’on la trouvera présentée ici, s’est progressivement dégagée, au cours du XIXe siècle et au début du XXe, de la théorie des équations linéaires (systèmes de n …   Encyclopédie Universelle

• Application multilinéaire — En algèbre linéaire, une application multilinéaire est une application à plusieurs variables vectorielles et à valeurs vectorielles qui est linéaire en chaque variable. Une application multilinéaire à valeurs scalaires est appelée forme… …   Wikipédia en Français

• Sous-espace supplémentaire — En mathématiques, plus précisément en algèbre linéaire, deux sous espaces vectoriels d un même espace vectoriel sont supplémentaires dans cet espace si tout vecteur de l espace se décompose de façon unique en une somme d un vecteur de chacun des… …   Wikipédia en Français

• Application Linéaire — En mathématiques, une application linéaire (aussi appelée opérateur linéaire ou transformation linéaire) est une application entre deux espaces vectoriels qui respecte l’addition des vecteurs et la multiplication scalaire définie dans ces espaces …   Wikipédia en Français