Theoreme des quatre sommets

Theoreme des quatre sommets

Théorème des quatre sommets

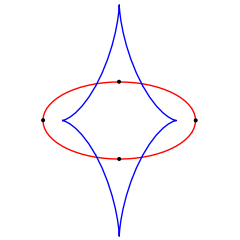Une ellipse (en rouge) et sa développée (en bleu), montrant les 4 sommets annulant k', chacun d'eux correspondant à un cusp de la développée.

Le théorème des 4 sommets consititue un résultat remarquable de géométrie différentielle quant aux propriétés globales des courbes fermées.

Sommaire

Énoncé

Énoncé dans le cas le plus simple

Soit γ une courbe fermée convexe, paramétrée par sa longueur s. Soit k(s) la courbure calculée au point γ(s). Alors il existe au moins 4 paramètres si pour lesquels k'(si) = 0.

La signification géométrique de ce résultat est que la courbure est soit constante, soit possède au moins 4 extrema. On pourra en trouver une démonstration dans [ManDoCar]

Cas général

Le théorème des 4 sommets à d'abord été démontré pour les courbes convexes (c'est-à-dire à courbure positive) en 1909 par Syamadas Mukhopadhyaya.[1] Sa preuve utilise le fait qu'un point de la courbe est un extremum de la fonction courbure si et seulement si le cercle osculateur en ce point possède un contact en 4 points avec la courbe (dans le cas général, le cercle osculateur possède 3 points de contact avec la courbe)). Le théorème des 4 sommets a été démontré dans le cas général par Adolf Kneser en 1912.[2]

Reciproque

La réciproque du théorème des quatre sommets énonce qu'une fonction continue, à valeur réelle, et ayant pour domaine de définition le cercle unité et qui par ailleurs possède 2 maxima locaux et 2 minima est la courbure d'une courbe simple et fermée du plan. La réciproque a été prouvée pour des fonctions strictement positives en 1971 par Herman Gluck, en tant que cas particulier d'un théorème plus général concernant le précalcul de la courbure sur une n-spheres.[3] La réciproque a été finalement démontrée dans le cas général par Björn Dahlberg peu de temps avant sa mort en Janvier 1998 et publiée à titre posthume.[4] La preuve de Dahlberg utilise principalement l'indice, argument que l'on retrouve par ailleurs dans certaine démonstration du théorème fondamental de l'algèbre.

Sources

  • [ManDoCar] (en) Manfredo Do Carmo, Differential geometry of curves and surfaces, Prentice-Hall, Rio de Janeiro, 1976, 503 p. (ISBN 0132125897) 

Notes et références

  1. ↑ S. Mukhopadhyaya, « New methods in the geometry of a plane arc », dans Bull. Calcutta Math. Soc., vol. 1, 1909, p. 21-27 
  2. ↑ Kneser, Adolf (1912). "Bemerkungen uber die Anzahl der Extrema des Krummung auf geschlossenen Kurven und uber verwandte Fragen in einer nicht eucklidischen Geometrie". Festschrift Heinrich Weber: 170-180, Teubner. 
  3. ↑ Herman Gluck, « The converse to the four-vertex theorem », dans L'Enseignement Math., vol. 17, 1971, p. 295-309 
  4. ↑ Björn Dahlberg, « The converse of the four vertex theorem », dans Proc. Amer. Math. Soc., vol. 133, no 7, 2005, p. 2131-2135 [texte intégral] 
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me des quatre sommets ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme des quatre sommets de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Théorème des quatre sommets — Une ellipse (en rouge) et sa développée (en bleu), montrant les 4 sommets annulant k , chacun d eux correspondant à un point de rebroussement de la développée. Le théorème des quatre sommets constitue un résultat remarquable de géométrie… …   Wikipédia en Français

  • Theoreme des quatre couleurs — Théorème des quatre couleurs Carte administrative de la Russie colorée avec quatre couleurs Le théorème des quatre couleurs affirme qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] …   Wikipédia en Français

  • Théorème des quatre couleurs — Vitrail coloré avec quatre couleurs Le théorème des quatre couleurs indique qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] n importe quelle carte découpée en régions connexes, de sorte que deux régions… …   Wikipédia en Français

  • Problème des quatre couleurs — Théorème des quatre couleurs Carte administrative de la Russie colorée avec quatre couleurs Le théorème des quatre couleurs affirme qu il est possible, en n utilisant que quatre couleurs différentes, de colorer[1] …   Wikipédia en Français

  • Théorème de carathéodory (géométrie) — Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé 2 Preuves 2.1 La preuve usuelle …   Wikipédia en Français

  • Théorème de Helly — dans le plan : si trois quelconques des convexes de la famille se rencontrent alors l intersection de tous ces convexes est non vide. Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par… …   Wikipédia en Français

  • Théorème de helly — Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par Eduard Helly, et il a été publié par Johann Radon en 1921[1],[2]. Énoncé Théorème …   Wikipédia en Français

  • Theoreme de Krein-Milman — Théorème de Krein Milman Le théorème de Krein Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par …   Wikipédia en Français

  • Théorème de krein-milman — Le théorème de Krein Milman est un théorème, démontré par Mark Krein et David Milman en 1940, qui généralise à certains espaces vectoriels topologiques un résultat géométrique portant sur les ensembles convexes énoncé par Hermann Minkowski en… …   Wikipédia en Français

  • Théorème de Radon (Géométrie) — Sommaire 1 Énoncé 2 Preuve 3 Théorème de Tverberg 4 Notes et références // …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”