Adherence, interieur et frontiere d'un convexe

Adhérence, intérieur et frontière d'un convexe

Dans le cas particulier de parties convexes d'un espace vectoriel topologique, les opérateurs topologiques élémentaires d'adhérence ou intérieur préservent la convexité. Sous une réserve technique mineure (qui justifie l'introduction de concepts simples, ceux d'intérieur relatif et de frontière relative, qui sont l'intérieur ou la frontière relativement à l'enveloppe affine du convexe), le remplacement d'un convexe par son adhérence ou son intérieur n'en modifie pas profondément la forme ; en particulier le bord du convexe reste discernable sur les nouveaux convexes ouvert ou fermé qu'on lui a substitués.

Sommaire

1 Observation préalable : le cadre de cet article
2 Adhérence d'un convexe
3 Intérieur et intérieur relatif d'un convexe
4 Frontière relative d'un convexe
5 Enchaînement d'opérations successives
6 Notes et références

Observation préalable : le cadre de cet article

Pour des raisons qui tiennent surtout à l'absence de vocabulaire usuel pour les espaces affines munis d'une topologie compatible avec leur structure géométrique, les résultats ci-dessous sont énoncés dans le contexte d'un « espace vectoriel topologique ». Dans les faits, c'est la structure affine de l'espace sous-jacent qui fait sens et tout ce qui est énoncé est valable à l'identique sous l'hypothèse qui serait bien lourde à énoncer d'un « espace affine dont l'espace vectoriel sous-jacent est muni d'une structure d'espace vectoriel topologique ».

En particulier, tout ce qui est écrit est valable dans le cadre des espaces affines de dimension finie. Le lecteur mal à l'aise en topologie générale mais au fait du vocabulaire de base concernant les espaces métriques pourra lire l'article en se restreignant mentalement à un tel cadre, suffisant pour survoler l'essentiel du contenu.

Les espaces sont toujours implicitement réels (il faudrait adapter certaines affirmations relatives aux dimensions dans le cas d'espaces vectoriels complexes).

Adhérence d'un convexe

Proposition — Dans un espace vectoriel topologique, l'adhérence d'un convexe est convexe.

Démonstration

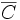Notons $C$ le convexe, et soit $x$ et $y$ deux points de $\overline C$ .

Soit maintenant $z$ un point du segment $[x, y]$ qui peut donc être écrit sous la forme $z = λ x + (1 - λ) y$ pour un certain $λ$ de $[0,1]$ .

Version simplifiée de la démonstration, valable pour les seuls espaces métrisables (et en particulier en dimension finie)

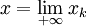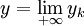On peut écrire $x=\lim_{+\infty }x_k$ et $y=\lim_{+\infty} y_k$ pour deux suites $(x k)$ et $(y k)$ de points de $C$ .

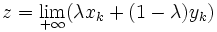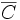Alors $z=\lim_{+\infty} (\lambda x_k+(1-\lambda) y_k)$ fournit une expression de $z$ comme limite de points de $C$ , ce qui assure bien l'appartenance de $z$ à $\overline C$ .

Version valable dans tout espace vectoriel topologique

Dans l'intention de montrer que $z$ appartient à 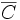$\overline C$ , prenons $W$ un voisinage arbitraire de $0$ dans $E$ et prouvons que $z + W$ rencontre $C$ .

L'application : 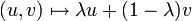$(u,v)\mapsto\lambda u+(1-\lambda) v$ est continue de 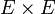$E\times E$ vers $E$ ; il existe donc des ouverts $U$ et $V$ tels que 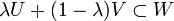$\lambda U+(1-\lambda) V\subset W$ . Comme $x + U$ est un ouvert contenant $x$ , il rencontre $C$ en au moins un point $x 1$ ; de même un $y 1$ près de $y$ . Le point $z 1 = λ x 1 + (1 - λ) y 1$ est alors à la fois dans $z + W$ par le choix même de $U$ et dans $C$ puisqu'il est sur un segment à extrémités dans $C$ .

Intérieur et intérieur relatif d'un convexe

Après s'être intéressé à l'adhérence d'un convexe, il est naturel d'examiner son intérieur. Or il apparaît ici une désagréable dissymétrie : alors que le remplacement d'un convexe $C$ par son adhérence conserve une partie significative de l'information sur la forme de celui-ci (ainsi, du moins en dimension finie, l'adhérence n'est qu'exceptionnellement l'espace ambiant $E$ tout entier, en fait dans le seul cas dégénéré où $C = E$ ) le remplacement par l'intérieur peut effacer toute information (l'intérieur étant souvent vide).

On a le choix entre deux solutions, plus ou moins adaptées selon le cas, pour contourner cet obstacle : l'une est de se restreindre dans les énoncés à des convexes dont l'enveloppe affine est l'espace ambiant tout entier^[1] —mais dans certains contextes, ce n'est guère pratique, par exemple si on veut évoquer les faces d'un polyèdre— ; l'autre est d'introduire un vocable supplémentaire :

Définition — L'intérieur relatif d'un convexe non vide $C$ dans un espace vectoriel topologique $E$ est l'intérieur de $C$ relativement au sous-espace affine engendré par $C$ .

Comme pour l'adhérence, on a :

Proposition — Dans un espace vectoriel topologique, l'intérieur et l'intérieur relatif d'un convexe sont convexes.

Démonstration

Vu la définition de l'intérieur relatif, il suffit de vérifier l'affirmation pour l'intérieur topologique usuel, dont l'intérieur relatif n'est qu'une manifestation.

Version simplifiée, valable dans le cadre d'un espace vectoriel normé

Notons $C$ le convexe, et soit $x$ et $y$ deux points de 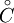$\stackrel{\circ}{C}$ . Comme $x$ est dans 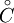$\stackrel{\circ}{C}$ , on peut introduire un $ε > 0$ assez petit pour que la boule ouverte $B (x,ε)$ soit incluse dans $C$ .

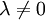Soit maintenant $z$ un point du segment $[x, y]$ qui peut donc être écrit sous la forme $z = λ x + (1 - λ) y$ pour un certain $λ$ de $[0,1]$ . Le cas où $z = y$ se traitant de manière triviale, on peut supposer que $\lambda\not=0$ .

On vérifie alors sans mal que la boule ouverte $B (z,λε)$ est incluse dans $C$ (pour qui veut les détails, un point de cette boule peut s'écrire $z + u$ pour un vecteur $u$ avec 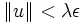$\|u\|<\lambda\epsilon$ ; or ce point $z + u$ est sur le segment $[x+{1\over\lambda}u,y]$ (c'est en effet le barycentre des extrémités de ce segment pour les poids respectifs $λ$ et $1 - λ$ ) ; les deux extrémités de ce segment sont dans le convexe $C$ c'est donc aussi le cas de $z + u$ , point du segment).

Le point $z$ est donc intérieur à $C$ .

Cas général Il n'y a presque rien à changer : au lieu d'introduire un $ε > 0$ , on introduit un voisinage de $0$ noté $U$ de sorte que $x + U$ se susbtitue à $B (x,ε)$ . Autour de $z$ , c'est alors le voisinage $z + λ U$ qui jouera le rôle que jouait $B (z,λε)$ dans la version précédente.

En dimension finie tout au moins, et contrairement à l'intérieur, l'intérieur relatif d'un convexe non vide n'est jamais vide :

Proposition — En dimension finie, l'intérieur relatif d'un convexe $C$ non vide n'est pas vide, et a la même dimension que $C$ .

Principe de la démonstration

Notons $d$ la dimension de $C$ et $F$ le sous-espace affine de dimension $d$ engendré par $C$ .

Il existe alors un $d + 1$ -uplet de points de $C$ constituant un repère affine de $F$ . L'ensemble des points à coordonnées barycentriques toutes strictement positives dans ce repère affine fournit alors la clé de la preuve : il n'est évidemment pas vide, et on vérifie facilement que tous ses points sont dans l'intérieur relatif de $C$ tout en étant assez nombreux pour engendrer affinement $F$ ; le sous-espace affine engendré par l'intérieur relatif de $C$ est donc bien au moins aussi gros que celui engendré par $C$ , d'où l'égalité des dimensions.

En guise de résumé de cette section, on peut faire un bilan rapide, $C$ désignant un convexe non vide d'un espace affine réel $E$ de dimension finie, on a l'alternative suivante :

ou bien 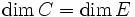$\mathrm{dim}\,C=\mathrm{dim}\,E$ , dans lequel cas intérieur et intérieur relatif sont un même convexe, qui engendre affinement $E$ ;
ou bien 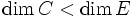$\mathrm{dim}\,C<\mathrm{dim}\,E$ , dans lequel cas l'intérieur ordinaire est vide, mais l'intérieur relatif est lui un convexe non vide, qui engendre affinement le même sous-espace affine que $C$ .

Frontière relative d'un convexe

De même que l'intérieur « ordinaire », la frontière n'est pas toujours un objet pertinent pour l'étude d'un convexe. Ainsi, pour un terrain rectangulaire vivant dans l'espace à trois dimensions, elle est bien décevante puisque égale à toute l'étendue du territoire.

On utilisera plutôt la frontière relative, définie à partir de l'intérieur relatif :

Définition — La frontière relative d'un convexe non vide $C$ dans un espace affine $E$ de dimension finie est le complémentaire de son intérieur relatif dans son adhérence.

Le concept est bien plus satisfaisant : dans l'exemple du terrain, il renvoie bien ce qu'évoque le mot « frontière » du langage courant.

On peut faire la remarque suivante^[2], d'intérêt surtout anecdotique dès lors que le théorème de Krein-Milman en fournit une variante nettement plus puissante :

Proposition — Un convexe compact (non vide et non réduit à un point) est l'enveloppe convexe de sa frontière relative (et a fortiori de sa frontière)

Démonstration

Soit $z$ un point du convexe $C$ . Traçons une droite affine $D$ qui passe par $z$ et qui est incluse dans le sous-espace affine engendré par $C$ . L'intersection 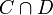$C\cap D$ est un convexe compact non vide de $D$ , donc un segment $[x, y]$ (où l'un des points $x$ ou $y$ , voire les deux, peut être confondu avec $z$ ). Il est facile de vérifier que $x$ comme $y$ n'appartient pas à l'intérieur relatif de $C$ . Les deux points sont donc sur la frontière relative, et $z$ est pour sa part dans l'enveloppe convexe de cette frontière.

La frontière contenant toujours la frontière relative, l'affirmation a fortiori est alors une évidence.

Enchaînement d'opérations successives

Dans cette section, on notera $cl(A)$ l'adhérence, $int(A)$ l'intérieur « ordinaire », $ir(A)$ l'intérieur « relatif ».

On sait que, pour des parties quelconques d'un espace topologique (et sans avoir besoin de chercher des contre-exemples bien compliqués), il faut accumuler pas moins de quatre opérateurs pour arriver à des formules justes :

cl(int(cl(int(A)))) = cl(int(A))

int(cl(int(cl(A)))) = int(cl(A))

Les choses se stabilisent beaucoup plus vites pour des convexes, comme l'exprime le théorème ci-dessous et son corollaire :

Théorème — Soit $C$ un convexe dans un espace vectoriel topologique. On suppose en outre $C$ d'intérieur non vide. Alors $int(cl(C)) = int(C)$ et $cl(int(C)) = cl(C)$ .

Corollaire — Pour un convexe non vide $C$ en dimension finie, $ir(cl(C)) = ir(C)$ et $cl(ir(C)) = cl(C)$ . En particulier les trois convexes emboîtés $ir(C)$ , $C$ et $cl(C)$ ont la même frontière relative.

Principe de la démonstration

La preuve peut se fonder agréablement sur le lemme suivant :

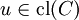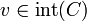si $u\in\mathrm{cl}(C)$ et $v\in\mathrm{int}(C)$ , alors $]u,v]\subset\mathrm{int}(C)$

dont on ne détaillera pas ici la preuve, facile si on a une bonne intuition graphique du problème.

Montrons par exemple comment la première affirmation se déduit du lemme. L'une des inclusions étant évidente, tout ce qu'il reste à faire est de prouver que tout point $x$ de $int(cl(C))$ est en fait un point de $int(C)$ . Pour ce, on profite de l'hypothèse de non-vacuité de $int(C)$ pour se saisir d'un $v$ auxiliaire lui appartenant. On peut ensuite affiner un $ε > 0$ suffisamment petit pour que, si on note $u = x + ε(x - v)$ le point $u$ soit dans $cl(C)$ . Comme on s'y est pris, $x$ est alors un point du segment $] u, v]$ auquel le lemme est applicable.

Notes et références

Sauf précision spécifique, l'ensemble de l'article a été élaboré à partir des pages 33 à 36 de Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of convex analysis, coll. « Grundlehren Text Editions », Springer, 2001 (ISBN 3540422056), complété par Jean Dieudonné, Élaments d'analyse, tome II, coll. « Cahiers scientifiques » fasc. XXXI, Gauthier-Villars, 1974, (ISBN 20400629X), exercice 11 p. 70 pour les énoncés valables dans tout espace vectoriel topologique.

↑ C'est par exemple le choix que fait Marcel Berger dans Marcel Berger, Géométrie [détail des éditions], section 11.3.
↑ Légèrement adaptée de la proposition 11.2.9 dans Marcel Berger, Géométrie [détail des éditions], tome 3, p. 29 dans l'édition de 1978.

Articles en rapport avec la convexité
Géométrie convexe	Article principal : Ensemble convexe Outils et résultats fondamentaux : Enveloppe convexe • Adhérence, intérieur et frontière d'un convexe • Projection sur un convexe fermé • Séparation des convexes • Points remarquables à la frontière d'un convexe • Polytope • Théorème de Krein-Milman • Lemme de Farkas Géométrie combinatoire : Théorème de Carathéodory • Théorème de Radon • Théorème de Helly Géométrie métrique : Courbe de largeur constante • Théorème des quatre sommets Algorithmes de géométrie convexe : Approche polyèdrale • Marche de Jarvis • Parcours de Graham • Théorème optimisation/séparation Optimisation linéaire : Programmation linéaire • Algorithme du simplexe • Génération de colonnes
Interactions géométrie-analyse	Théorème de Hahn-Banach • Jauge
Analyse convexe	Article principal : Fonction convexe Outils et résultats fondamentaux : Inégalité de Jensen Optimisation convexe : Conditions de Kuhn-Tucker • Méthode du point intérieur
Utilisations de la convexité	Inégalités de convexité : Inégalité arithmético-géométrique • Inégalité de Hölder Analyse fonctionnelle : Espace localement convexe • Théorème du point fixe de Schauder Localisation de zéros de polynômes : Théorème de Gauss-Lucas Théorie des nombres : Théorème de Minkowski

Portail des mathématiques

Ce document provient de « Adh%C3%A9rence, int%C3%A9rieur et fronti%C3%A8re d%27un convexe ».

Catégories : Géométrie convexe | Espace vectoriel topologique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Adherence, interieur et frontiere d'un convexe de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Adhérence, intérieur et frontière d'un convexe — Dans le cas particulier de parties convexes d un espace vectoriel topologique, les opérateurs topologiques élémentaires d adhérence ou intérieur préservent la convexité. Sous une réserve technique mineure (qui justifie l introduction de concepts… … Wikipédia en Français
Points et parties remarquables de la frontiere d'un convexe — Points et parties remarquables de la frontière d un convexe Face à un polyèdre convexe de l espace de dimension 3, qu il soit familier comme un cube ou plus exotique, on sait spontanément reconnaître des points où le convexe est… … Wikipédia en Français
Points et parties remarquables de la frontière d'un convexe — Face à un polyèdre convexe de l espace de dimension 3, qu il soit familier comme un cube ou plus compliqué, on sait spontanément reconnaître les points où le convexe est « pointu », ses sommets, puis subdiviser les points restants entre … Wikipédia en Français
Frontiere relative d'un convexe — Frontière relative d un convexe Cet article court présente un sujet plus amplement développé ici : Adhérence, intérieur et frontière d un convexe. La frontière relative d un convexe C est la frontière de C relativement à son enveloppe affine … Wikipédia en Français
Interieur relatif d'un convexe — Intérieur relatif d un convexe Cet article court présente un sujet plus amplement développé ici : Adhérence, intérieur et frontière d un convexe. L intérieur relatif d un convexe C est l intérieur de C relativement à son enveloppe affine. Ce … Wikipédia en Français
Intérieur relatif d'un convexe — Cet article court présente un sujet plus amplement développé ici : Adhérence, intérieur et frontière d un convexe. L intérieur relatif d un convexe C est l intérieur de C relativement à son enveloppe affine. Ce document provient de «… … Wikipédia en Français
Adherence (mathematiques) — Adhérence (mathématiques) Pour les articles homonymes, voir Adhérence. En topologie, l adhérence d une partie d un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la… … Wikipédia en Français
Adhérence (Mathématiques) — Pour les articles homonymes, voir Adhérence. En topologie, l adhérence d une partie d un espace topologique est le plus petit ensemble fermé contenant cette partie. On retrouve cette notion particulièrement dans la convergence de suites dans les… … Wikipédia en Français
Interieur (topologie) — Intérieur (topologie) Pour les articles homonymes, voir intérieur. En mathématiques, l intérieur est une notion de topologie appliquée à une partie d un espace topologique ou à une variété à bord. Dans le premier cas, l intérieur d une partie est … Wikipédia en Français
Intérieur (mathématiques) — Intérieur (topologie) Pour les articles homonymes, voir intérieur. En mathématiques, l intérieur est une notion de topologie appliquée à une partie d un espace topologique ou à une variété à bord. Dans le premier cas, l intérieur d une partie est … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Adherence, interieur et frontiere d'un convexe

Adhérence, intérieur et frontière d'un convexe

Sommaire

Observation préalable : le cadre de cet article

Adhérence d'un convexe

Intérieur et intérieur relatif d'un convexe

Frontière relative d'un convexe

Enchaînement d'opérations successives

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Adherence, interieur et frontiere d'un convexe

Adhérence, intérieur et frontière d'un convexe

Sommaire

Observation préalable : le cadre de cet article

Adhérence d'un convexe

Intérieur et intérieur relatif d'un convexe

Frontière relative d'un convexe

Enchaînement d'opérations successives

Notes et références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link