Theoreme du point fixe de Schauder

Théorème du point fixe de Schauder

Le théorème de Schauder, prouvé en 1930 par le mathématicien polonais Juliusz Schauder est un puissant théorème du point fixe intervenant dans la démonstration de l'existence de solutions à une équation différentielle.

Énoncé

Soit $E$ un espace vectoriel normé sur 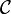$\mathbb{R}$ , $\mathcal{C}$ une partie non vide de $E$ , convexe, fermée et bornée.

Si $T$ est une application continue de $C$ dans $C$ telle que $T (C)$ soit relativement compact, alors $T$ a un point fixe

Preuve

Notons 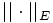$||\cdot||_E$ la norme de $E$ .

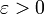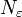Soit $\varepsilon > 0$ . $T (C)$ étant une partie relativement compacte de $C$ , il est précompact, on peut donc recouvrir $T (C)$ à l'aide d'un nombre fini de boules de rayon $\varepsilon$ . Autrement dit, il existe $N_\varepsilon$ un nombre entier, et 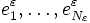$e_1^\varepsilon, \dots, e_{N_\varepsilon}^\varepsilon$ dans $C$ tels que :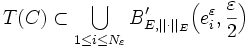

$T(C) \subset \bigcup_{1 \leq i \leq N_\varepsilon} B_{E,||\cdot||_E}^{\prime} \Big( e_i^\varepsilon, \frac{\varepsilon}{2}\Big)$

On définit alors pour tout $i \in \{1, 2, \dots, N_{\varepsilon}\}$ l'application $π i,ε$ de $C$ dans $\mathbb{R}$ par :

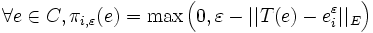
$\forall e \in C, \pi_{i,\varepsilon} (e) = \max \Big(0, \varepsilon - ||T(e) - e_i^\varepsilon||_E\Big)$

Chacune de ces applications est bien continue. On définit alors l'application continue $T_\varepsilon$ par :

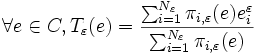
$\forall e \in C, T_\varepsilon(e) = \frac{\sum_{i=1}^{N_\varepsilon} \pi_{i,\varepsilon}(e)e_i^\varepsilon}{\sum_{i=1}^{N_\varepsilon} \pi_{i,\varepsilon}(e)}$

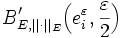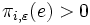Tout d'abord, cette formule est bien définie, car le dénominateur n'est jamais nul. En effet, $T (e)$ est dans l'une des boules $B_{E,||\cdot||_E}^{\prime} \Big( e_i^\varepsilon, \frac{\varepsilon}{2}\Big)$ et donc pour ce $i$ , $\pi_{i,\varepsilon}(e) > 0$ .

Par ailleurs 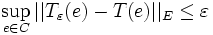$\sup_{e \in C} ||T_\varepsilon(e) - T(e)||_E \leq \varepsilon$ . En effet, en notant 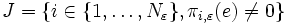$J = \{i \in \{1, \dots, N_\varepsilon \}, \pi_{i , \varepsilon}(e) \neq 0\}$ , on vérifie que si 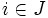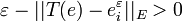$i \in J$ , $\varepsilon - ||T(e) - e_i^\varepsilon||_E > 0$ et :

$||T_\varepsilon(e) - T(e)||_E \leq \Big( \sum_{i \in J} \pi_{i,\varepsilon}(e) \Big)^{-1} \Big( \sum_{i \in J} \pi_{i,\varepsilon}(e) ||e_i^\varepsilon - T(e)||_E\Big) \leq \varepsilon$

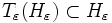Posons alors $H_\varepsilon = C \cap (\mathbb{R}e_1^\varepsilon + \cdots + \mathbb{R}e_{N_\varepsilon}^\varepsilon)$ . La définition même de $T_\varepsilon$ nous assure que $T_\varepsilon(H_\varepsilon) \subset H_\varepsilon$ .

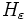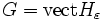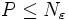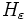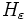$H_\varepsilon$ est un sous-ensemble fermé, borné, convexe, symétrie, inclus dans le sous-espace $G = \textrm{vect} H_\varepsilon$ de dimension finie $P \leq N_\varepsilon$ . On peut donc extraire de $H_\varepsilon$ une base $(e_1, \dots, e_P)$ de $G$ . Supposons à présent que $H_\varepsilon$ contient plus de deux éléments. Alors 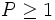$P \geq 1$ . Montrons que 0 est à l'intérieur de 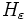$H_\varepsilon$ , considéré en tant que partie de $G$ . Les normes sur $G$ étant équivalentes ( $G$ est de dimension finie), on peut considérer la norme $N$ définie par 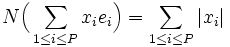$N\Big(\sum_{1 \leq i \leq P} x_ie_i\Big) = \sum_{1 \leq i \leq P} |x_i|$ . 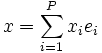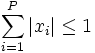Si $N(x) \leq 1$ , on peut écrire $x = \sum_{i=1}^P x_ie_i$ , où $\sum_{i=1}^P |x_i| \leq 1$ . 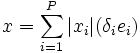Posons alors $x i = δ i | x i |$ , où $\delta_i = \pm 1$ , alors $x = \sum_{i=1}^P |x_i| (\delta_i e_i)$ , donc $x$ est barycentre convexe des $δ i e i$ qui sont dans 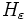$H_\varepsilon$ (on rappelle que 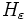$H_\varepsilon$ est symétrique et convexe). Il en résulte que 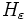$H_\varepsilon$ contient la boule pour $N$ de centre 0 et de rayon 1. 0 est bien à l'intérieur de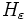 $H_\varepsilon$

On définit l'application $ρ$ de $G$ dans 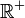$\mathbb{R}^+$ par la formule :

$\forall a \in G, \rho(a) = \inf \Big\{ \eta \in \R_+^*, \frac{1}{\eta} a \in H_\varepsilon \Big\}$

Tout d'abord, comme $0$ appartient à l'intérieur de $G$ , la fonction $ρ$ est bien définie. On montre (par un raisonnement fastidieux, mais non difficile) que c'est une norme pour $G$ , dont la boule unité n'est rien d'autre que 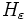$H_\varepsilon$ . 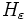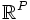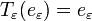Ainsi $H_\varepsilon$ est homéomorphe à la boule unité de $\mathbb{R}^P$ (dans le cas où $P = 0$ , c'est évident), et l'application directe du théorème du point fixe de Brouwer dit qu'il existe un vecteur $e_\varepsilon \in H_\varepsilon$ tel que $T_\varepsilon(e_\varepsilon) = e_\varepsilon$ .

On peut appliquer tout ce long raisonnement pour 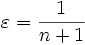$\varepsilon = \frac{1}{n+1}$ , on dispose alors d'une suite d'éléments $(x n)$ de C tels que :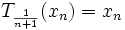

$T_{\frac{1}{n+1}}(x_n) = x_n$

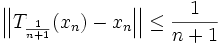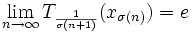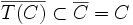D'autre part, on sait que $\Big|\Big| T_{\frac{1}{n+1}}(x_n) - x_n \Big|\Big| \leq \frac{1}{n+1}$ . Comme $T (C)$ est relativement compact, $\overline{T(C)}$ est compact, on peut extraire de $(T (x n))$ une sous-suite $(T σ(n))$ convergente. Notons $e$ sa limite, on a alors $\lim_{n \to \infty} T_{\frac{1}{\sigma(n+1)}}(x_{\sigma(n)}) = e$ donc $T (e) = e$ . $e$ est bien dans $C$ car $\overline{T(C)} \subset \overline{C} = C$ .

Référence

Écoles normales supérieures. Sujet commun Paris-Lyon. 1998.

Articles en rapport avec la convexité
Géométrie convexe	Article principal : Ensemble convexe Outils et résultats fondamentaux : Enveloppe convexe • Adhérence, intérieur et frontière d'un convexe • Projection sur un convexe fermé • Séparation des convexes • Points remarquables à la frontière d'un convexe • Polytope • Théorème de Krein-Milman • Lemme de Farkas Géométrie combinatoire : Théorème de Carathéodory • Théorème de Radon • Théorème de Helly Géométrie métrique : Courbe de largeur constante • Théorème des quatre sommets Algorithmes de géométrie convexe : Approche polyèdrale • Marche de Jarvis • Parcours de Graham • Théorème optimisation/séparation Optimisation linéaire : Programmation linéaire • Algorithme du simplexe • Génération de colonnes
Interactions géométrie-analyse	Théorème de Hahn-Banach • Jauge
Analyse convexe	Article principal : Fonction convexe Outils et résultats fondamentaux : Inégalité de Jensen Optimisation convexe : Conditions de Kuhn-Tucker • Méthode du point intérieur
Utilisations de la convexité	Inégalités de convexité : Inégalité arithmético-géométrique • Inégalité de Hölder Analyse fonctionnelle : Espace localement convexe • Théorème du point fixe de Schauder Localisation de zéros de polynômes : Théorème de Gauss-Lucas Théorie des nombres : Théorème de Minkowski

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me du point fixe de Schauder ».

Catégories : Théorème de mathématiques | Espace vectoriel normé

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme du point fixe de Schauder de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Théorème du point fixe de schauder — Le théorème de Schauder, prouvé en 1930 par le mathématicien polonais Juliusz Schauder est un puissant théorème du point fixe intervenant dans la démonstration de l existence de solutions à une équation différentielle. Énoncé Soit E un espace… … Wikipédia en Français
Théorème du point fixe de Schauder — Le théorème du point fixe de Schauder, prouvé en 1930 par le mathématicien polonais Juliusz Schauder est un puissant théorème du point fixe intervenant dans la démonstration de l existence de solutions à une équation différentielle. Énoncé Soit E … Wikipédia en Français
Théorème du point fixe de Brouwer — En 1886 Henri Poincaré démontre un résultat équivalent au théorème du point fixe de Brouwer. L énoncé exact est prouvé pour la dimension trois par Piers Bohl pour la première fois en 1904, puis par Jacques Hadamard dans le cas général en 1910.… … Wikipédia en Français
Théorème du point fixe — Théorèmes de point fixe En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques,… … Wikipédia en Français
Theoremes de point fixe — Théorèmes de point fixe En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques,… … Wikipédia en Français
Théorèmes de point fixe — En analyse, un théorème de point fixe est un résultat qui permet d affirmer qu une fonction f admet sous certaines conditions un point fixe. Ces théorèmes se révèlent être des outils très utiles en mathématiques, principalement dans le domaine de … Wikipédia en Français
Théorème de Shauder — Théorème du point fixe de Schauder Le théorème de Schauder, prouvé en 1930 par le mathématicien polonais Juliusz Schauder est un puissant théorème du point fixe intervenant dans la démonstration de l existence de solutions à une équation… … Wikipédia en Français
Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… … Wikipédia en Français
Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… … Wikipédia en Français
Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoreme du point fixe de Schauder

Théorème du point fixe de Schauder

Énoncé

Preuve

Référence

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Theoreme du point fixe de Schauder

Théorème du point fixe de Schauder

Énoncé

Preuve

Référence

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link