Théorème de Radon (Géométrie)

Théorème de Radon (Géométrie)

Théorème de Radon (géométrie)

Sommaire

Énoncé

Le théorème de Radon, ou lemme de Radon, sur les ensembles convexes affirme que tout ensemble 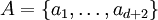A = \{a_1, \dots, a_{d+2}\} contenant d + 2 éléments de 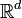\mathbb{R}^{d} admet une partition en deux parties A1,A2 dont les enveloppes convexes Conv(A1) et Conv(A2) se rencontrent. Une telle partition est alors appelée partition de Radon, et un point de l'intersection des enveloppes est appelé point de Radon (il ne s'agit pas a priori d'un des points ai).

Prenons l'exemple d = 2. Dans ce cas l'ensemble A est constitué de quatre points. La partition de A peut donner un ensemble de trois points et un singleton, les premiers formant un triangle contenant le dernier point. Ou alors la partition consiste en deux ensembles constitués chacun de deux points, les segments s'intersectant en un point.

Ce résultat a été publié pour la première fois par Johann Radon en 1921[1]. Il y apparaît comme résultat intermédiaire dans la preuve du théorème de Helly, ce qui explique la dénomination courante de lemme[2].

Preuve

On suppose que 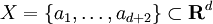X = \{a_1,\dots,a_{d+2}\}\subset \mathbf{R}^d. Considérons le système :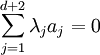

\sum_{j=1}^{d+2} \lambda_j a_j=0

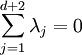
\sum_{j=1}^{d+2} \lambda_j=0

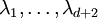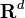d'inconnues réelles \lambda_1,\dots,\lambda_{d+2} : il équivaut à un système linéaire de d + 1 équations à d + 2 inconnues a_1,a_2,\dots,a_{d+2}, puisque la première équation, si on la développe en un système pour chaque composante des ai (vecteurs dans \mathbf{R}^d), se transforme aussitôt en d équations linéaires traditionnelles. Il existe donc une solution non nulle de ce système. Fixons 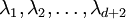\lambda_1,\lambda_2,\dots,\lambda_{d+2} une telle solution. Posons alors :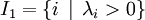

I_1 = \{i\,\mid\, \lambda_i > 0\}

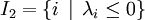
I_2 = \{i\,\mid\, \lambda_i \leq 0\}

Puisque la somme des λi est nulle alors que les λi ne sont pas tous nuls, I et J ne sont pas vides.

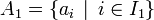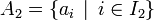La partition requise de A est alors A_1=\{a_i\,\mid\, i\in I_1\} et A_2=\{a_i\,\mid\, i\in I_2\}. En effet, il est immédiat de vérifier à partir du système, que :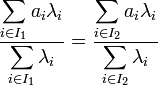

\frac{\displaystyle\sum_{i\in I_1} a_i \lambda_i}{\displaystyle\sum_{i\in I_1} \lambda_i} = \frac{\displaystyle\sum_{i\in I_2} a_i \lambda_i}{\displaystyle\sum_{i\in I_2} \lambda_i}

et cette formule fournit un point commun aux enveloppes convexes de A1 et de A2.

Théorème de Tverberg

Helge Tverberg a démontré en 1966 une généralisation de ce théorème pour des partitions de A en r sous-ensembles. Le théorème de Tverberg affirme que :

Un ensemble A de 1 + (d + 1)(r − 1) points de 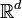\mathbb{R}^d admet une partition en r sous-ensembles dont l'intersection des enveloppes convexes n'est pas vide

Notes et références

  1. ↑ Johann Radon, Mengen konvexer körper, die einen gemeinsamen Punkt enthalten, Math. Ann., 83:113-115, 1921
  2. ↑ Jiri Matousek, Lectures on Discrete Geometry, Graduate Texts in Mathematics, Springer, 2002
  • H. G. Eggleston, Convexity, Cambridge Univ. Press.
  • S. R. Lay, Convex Sets and Their Applications, Wiley.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Radon (g%C3%A9om%C3%A9trie) ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Radon (Géométrie) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Théorème de radon (géométrie) — Sommaire 1 Énoncé 2 Preuve 3 Théorème de Tverberg 4 Notes et références // …   Wikipédia en Français

  • Théorème de Radon (géométrie) — Sommaire 1 Énoncé 2 Preuve 3 Théorème de Tverberg 4 Notes et références Énoncé Le théorème de …   Wikipédia en Français

  • Théorème de carathéodory (géométrie) — Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé 2 Preuves 2.1 La preuve usuelle …   Wikipédia en Français

  • Théorème de Carathéodory (géométrie) —  Ne pas confondre avec le théorème d extension de Carathéodory. Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé …   Wikipédia en Français

  • Théorème de Helly — dans le plan : si trois quelconques des convexes de la famille se rencontrent alors l intersection de tous ces convexes est non vide. Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par… …   Wikipédia en Français

  • Théorème de helly — Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par Eduard Helly, et il a été publié par Johann Radon en 1921[1],[2]. Énoncé Théorème …   Wikipédia en Français

  • Theoreme de Minkowski — Théorème de Minkowski En mathématiques, le théorème de Minkowski est un résultat concernant la géométrie des réseaux. Il relie le nombre de points du réseau contenu dans une partie convexe symétrique au volume fondamental du réseau. Ce théorème… …   Wikipédia en Français

  • Théorème de minkowski — En mathématiques, le théorème de Minkowski est un résultat concernant la géométrie des réseaux. Il relie le nombre de points du réseau contenu dans une partie convexe symétrique au volume fondamental du réseau. Ce théorème est utilisé en théorie… …   Wikipédia en Français

  • Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… …   Wikipédia en Français

  • Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”