- Jauge (mathématiques)
-
Jauge (mathématiques)
 Pour les articles homonymes, voir jauge.
Pour les articles homonymes, voir jauge.Sommaire
Définition
Soit E un espace vectoriel sur
 ou sur
ou sur 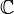 , qu'on supposera topologique chaque fois que nécessaire, et soit C une partie convexe de E contenant l'origine.
, qu'on supposera topologique chaque fois que nécessaire, et soit C une partie convexe de E contenant l'origine.
On appelle jauge de C la fonction p de E dans définie, pour chaque point x de E, par :
définie, pour chaque point x de E, par : ,
,
définition qu'on complète en posant
 si l'ensemble ci-dessus est vide.
si l'ensemble ci-dessus est vide.Faisons tout de suite une remarque de vérification immédiate, qui aide à interpréter ce qu'est la jauge :
Remarque —
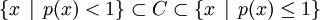 ;
;- si C est ouvert dans E, alors
 ;
;
- si C est fermé dans E, alors
 .
.
Propriétés de la jauge
Convexité de la jauge
On vérifie facilement :
Proposition — La jauge est sous-linéaire, et est par conséquent une fonction convexe.
Jauges ne prenant pas la valeur

La remarque suivante est immédiate :
Remarque — La jauge d'un convexe C contenant 0 ne prend que des valeurs finies si et seulement si C est absorbant.
Il est également immédiat de vérifier que cette condition est en particulier réalisée si 0 est intérieur à C ; la réciproque est vraie en dimension finie et facile à vérifier — on peut le faire assez élégamment en remarquant qu'en tant que fonction convexe à valeurs finies et définie partout, p est alors continue, et que
 est alors un voisinage de 0 contenu dans C.
est alors un voisinage de 0 contenu dans C.Lorsque 0 est intérieur à C, on peut se faire une image mentale simple de la jauge via ses surfaces de niveau : l'ensemble des points où elle prend la valeur 1 est exactement la frontière du convexe ; les surfaces de niveau pour les autres valeurs strictement positives sont les homothétiques de cette frontière ; en les éventuels points restant non couverts par la réunion de ces surfaces de niveau, la jauge prend la valeur 0.
On peut enfin remarquer que (pour un espace vectoriel réel), si C est symétrique par rapport à 0 avec une jauge évitant la valeur
 , la jauge est alors une semi-norme ; il en est de même pour un espace vectoriel complexe si on exige une version améliorée de la symétrie, à savoir l'invariance sous multiplication par n'importe quel complexe de module 1.
, la jauge est alors une semi-norme ; il en est de même pour un espace vectoriel complexe si on exige une version améliorée de la symétrie, à savoir l'invariance sous multiplication par n'importe quel complexe de module 1.Jauges ne prenant pas la valeur 0 hors de l'origine
Il est clair au vu de la définition que la jauge prend la valeur 0 en un point x0 autre que l'origine si et seulement si toute la demi-droite issue de l'origine et passant par x0 est incluse dans le convexe.
Il est dès lors immédiat que (dans un espace vectoriel normé) la jauge d'un convexe borné ne prend pas la valeur 0 hors de l'origine.
La réciproque est vraie pour un convexe fermé en dimension finie, et se démontrerait en exploitant la compacité de la sphère de rayon 1 :
Proposition — Soit C un convexe fermé contenant 0 dans un espace de dimension finie. Alors C est borné si et seulement si sa jauge ne prend pas la valeur 0 hors de l'origine.
À quoi servent les jauges ?
- Dans la théorie des espaces vectoriels topologiques, c'est par l'introduction d'une collection appropriée de jauges qu'on peut caractériser les espaces localement convexes en termes de semi-normes.
- En géométrie des convexes, la jauge est un outil intéressant pour ramener un problème purement géométrique (recherche d'un hyperplan) à un problème analytique (recherche d'une équation de l'hyperplan). Ainsi dans la preuve de la « forme géométrique » du théorème de Hahn-Banach —fondement de toute la théorie de la séparation des convexes et des hyperplans d'appui—, un pas essentiel est la constatation qu'exiger de l'hyperplan d'équation f(x) = 1 qu'il évite un convexe donné (ouvert et contenant 0), c'est la même chose que de demander à f de vérifier l'inéquation
 , p désignant la jauge du convexe.
, p désignant la jauge du convexe.
Références
Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of convex analysis, coll. « Grundlehren Text Editions », Springer, 2001 (ISBN 3540422056), p. 128-130
- Portail des mathématiques
Catégories : Géométrie convexe | Analyse convexe
Wikimedia Foundation. 2010.
