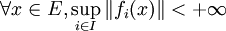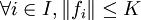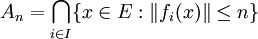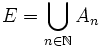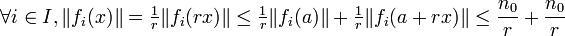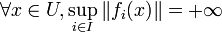Théorème de banach-steinhaus

Théorème de Banach-Steinhaus

Le théorème de Banach-Steinhaus (aussi appelé Principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn-Banach et le théorème de Banach-Schauder, des résultats fondamentaux de l'analyse fonctionnelle. Il a été publié en 1927 par Stefan Banach et Hugo Steinhaus, mais il a aussi été prouvé indépendamment par Hans Hahn.

Il affirme qu'une famille d'applications linéaires continues définies sur un espace de Banach est uniformément bornée si et seulement si elle est ponctuellement bornée. C'est une conséquence très importante de la propriété de Baire, qui se généralise d'ailleurs aux espaces de Fréchet.

Le théorème

Énoncé

Soit $E$ un espace de Banach et $F$ un espace vectoriel normé. On considère une famille 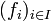$(f_i)_{i \in I}$ d'applications linéaires continues de $E$ dans $F$ . On suppose que cette famille est ponctuellement bornée, c'est-à-dire :

$\forall x \in E, \sup_{i \in I} \|f_i(x)\| < + \infty$

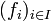Alors $(f_i)_{i \in I}$ est uniformément bornée, c'est-à-dire qu'il existe une constante $K$ telle que :

$\forall i \in I, \|f_i\| \leq K$

Démonstration

La preuve repose sur le fait qu'un espace de Banach est un espace de Baire, c'est-à-dire que toute réunion dénombrable de fermés d'intérieur vide est d'intérieur vide.

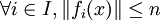Considérons $A n$ l'ensemble des éléments de $E$ tels que $\forall i \in I, \|f_i(x)\| \leq n$ .

$A_n = \bigcap_{i \in I} \{x \in E : \|f_i(x)\| \leq n\}$

$A n$ est une intersection de fermés, c'est donc un fermé. La famille 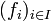$(f_i)_{i \in I}$ est ponctuellement bornée, cette hypothèse se traduit par l'égalité ensembliste :

$E = \bigcup_{n \in \mathbb{N}} A_n$

Comme $E$ n'est pas d'intérieur vide, il existe 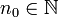$n_0 \in \mathbb{N}$ tel que 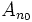$A_{n_0}$ ne soit pas d'intérieur vide : il contient une boule de centre $a$ et de rayon $r > 0$ .

Prenons un point $x$ de $E$ situé dans la boule unité fermée :

$\forall i \in I, \|f_i(x)\| = \tfrac 1r \|f_i(rx)\| \leq \tfrac 1r \|f_i(a)\| + \tfrac 1r \|f_i(a + rx)\| \leq \frac{n_0}r+\frac{n_0}r$

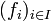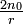c'est-à-dire : $(f_i)_{i \in I}$ est uniformément bornée (par $\tfrac{2n_0}r$ ).

Variante "forte" de l'énoncé

On a en fait démontré le résultat suivant. Avec les mêmes notations que ci-dessus, l'alternative est :

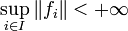
ou bien $\sup_{i \in I} \Vert f_i \Vert <+\infty$

ou bien il existe un résiduel U (c’est-à-dire une intersection dénombrable d'ouverts denses ; une telle partie est dense d'après le théorème de Baire) tel que

$\forall x\in U, \sup_{i \in I}\Vert f_i(x)\Vert=+\infty$

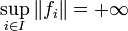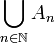En effet, la démonstration précédente montre que, si $\sup_{i \in I} \Vert f_i \Vert =+\infty$ , alors nécessairement, chaque $A n$ est un fermé d'intérieur vide. Il suffit alors de prendre pour U le complémentaire de $\bigcup_{n \in \mathbb{N}} A_n$ .

Exemples d'applications

Limite d'une suite d'applications linéaires continues

Mentionnons un corollaire très important du théorème de Banach-Steinhaus : si $(f n)$ est une suite d'applications linéaires continues de l'espace de Banach $E$ dans l'espace vectoriel normé $F$ qui converge simplement vers une fonction $f$ , alors $f$ est également une application linéaire continue.

En effet, la linéarité provient d'un simple passage à la limite. Et pour tout 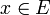$x \in E$ , $(f n (x))$ converge, c'est donc une suite bornée, et le théorème de Banach-Steinhaus affirme que $(f n)$ est uniformément bornée. $(f n)$ est bornée en norme subordonnée par une constante $C$ , et par passage à la limite des inégalités $f$ est bornée de norme subordonnée inférieure à $C$ .

Application aux sommes de Riemann

Article détaillé : somme de Riemann.

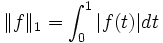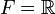Soit $E$ l'espace des fonctions continues sur $[0,1]$ à valeurs réelles, muni de la norme $\| f \|_1 = \int_0^1 |f(t)| dt$ , et $F = \mathbb R$ . Pour chaque entier 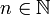$n\in\mathbb{N}$ , soit $u n$ l'opérateur défini par :

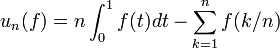$u_n(f) = n \int_0^1 f(t) dt - \sum_{k=1}^n f(k/n)$ .

Pour toute fonction $f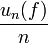$ , ${u_n(f) \over n}$ n'est autre que l'erreur commise dans le calcul de l'intégrale de $f$ lorsque l'on prend une somme de Riemann correspondant à une subdivision régulière de $[0,1]$ en $n$ intervalles égaux. Cette erreur est un 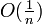$O(\tfrac1n)$ pour les fonctions de classe $C 1$ ou lipschitziennes, mais il n'en est pas de même pour les fonctions continues en général. En effet, on montre que 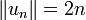$\| u_n \| = 2n$ , de sorte que 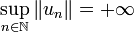$\sup_{n\in \mathbb N} \| u_n \| = + \infty$ et donc que le complémentaire de $A$ est dense. 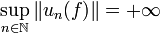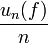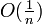Une fonction $f$ appartenant à ce complémentaire vérifie donc $\sup_{n\in \mathbb N} \|u_n(f)\| = + \infty$ , ce qui signifie que l'ensemble $u n (f)$ n'est pas borné et donc que l'erreur commise ${u_n(f) \over n}$ n'est pas un $O(\tfrac1n)$ .

Le théorème de Banach-Steinhaus donne une preuve de l'existence d'objets vérifiant telle ou telle propriété, mais cette preuve n'est pas constructive.

Application aux séries de Fourier

Article détaillé : noyau de Dirichlet.

Si $f$ est une fonction (disons continue) de période 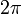$2\pi\,$ , on vérifie que la somme partielle $n$ -ième de sa série de Fourier est

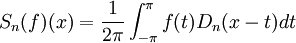$S_n(f)(x)=\frac{1}{2\pi}\int_{-\pi}^\pi f(t)D_n(x-t)dt$ , avec 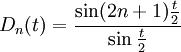$D_n(t)=\frac{\sin (2n+1)\frac{t}{2}}{\sin\frac{t}{2}}$ (noyau de Dirichlet)

Pour $n$ fixé, la norme de l'application 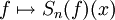$f\mapsto S_n(f)(x)$ , vue comme forme linéaire sur l'espace des fonctions continues et de période $2π$ , muni de la norme sup, est égale à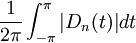 $\frac{1}{2\pi}\int_{-\pi}^\pi \vert D_n(t)\vert dt$

On vérifie que le nombre 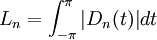$L_n=\int_{-\pi}^\pi \vert D_n(t)\vert dt$ appelé constante de Lebesgue, tend vers l'infini comme $log(n)$ .

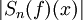D'après le théorème de Banach-Steinhaus, il existe donc une fonction $f\,$ telle que $\vert S_n(f)(x)\vert$ tende vers l'infini quand $n\,$ tend vers l'infini. Ainsi, la série de Fourier de $f\,$ diverge en $x\,$ .

Si on utilise la version forte du théorème de Banach-Steinhaus, on voit même que l'ensemble des fonctions continues de période 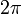$2\pi\,$ dont la série de Fourier diverge en $x\,$ est dense pour la topologie de la convergence uniforme.

Cet argument est d'autant plus remarquable qu'il n'est pas très facile de trouver des exemples explicites.

Voir aussi

Stefan Banach, Hugo Steinhaus, "Sur le principle de la condensation de singularités". Fundamenta Mathematicae

Applications du Théorème de Banach-Steinhaus sur la boite à Baire.

Théorèmes de l'analyse fonctionnelle

Théorème d'Ascoli • Théorème de Baire • Théorème de Banach-Alaoglu • Théorème de Banach-Mazur • Théorème de Banach-Schauder • Théorème de Banach-Steinhaus • Théorème du graphe fermé • Théorème de Hahn-Banach • Théorème de Lax-Milgram

modifier

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Banach-Steinhaus ».

Catégories : Théorème d'analyse | Espace vectoriel normé

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de banach-steinhaus de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Theoreme de Banach-Steinhaus — Théorème de Banach Steinhaus Le théorème de Banach Steinhaus (aussi appelé Principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn Banach et le théorème de Banach Schauder, des résultats fondamentaux de l analyse… … Wikipédia en Français
Théorème de Banach-Steinhaus — Le théorème de Banach Steinhaus (aussi appelé principe de la borne uniforme) fait partie, au même titre que le théorème de Hahn Banach et le théorème de Banach Schauder, des résultats fondamentaux de l analyse fonctionnelle. Il a été publié en… … Wikipédia en Français
Theoreme de Banach-Schauder — Théorème de Banach Schauder En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces… … Wikipédia en Français
Théorème de banach-schauder — En analyse fonctionnelle, le théorème de Banach Schauder, également appelé théorème de l application ouverte est un résultat fondamental qui affirme qu une application linéaire continue surjective entre deux espaces vectoriels normés complets est … Wikipédia en Français
Theoreme de Banach-Alaoglu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Theoreme de Banach-Mazur — Théorème de Banach Mazur Le théorème de Banach Mazur est un outil d analyse fonctionnelle. De manière très approximative, il exprime que les espaces vectoriels normés vérifiant des conditions raisonnables du point de vue de l analyse sont des… … Wikipédia en Français
Théorème de Banach-Alaoglu — Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie… … Wikipédia en Français
Théorème de Banach-Alaoğlu — Théorème de Banach Alaoglu Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie… … Wikipédia en Français
Théorème de banach-alaoglu — Bourbaki Le théorème de Banach Alaoglu Bourbaki est un résultat de compacité en analyse fonctionnelle. Si E est un espace vectoriel topologique et V un voisinage ouvert de 0, le polaire de V, défini par est une partie compacte pour la topologie… … Wikipédia en Français
Théorème de banach-mazur — Le théorème de Banach Mazur est un outil d analyse fonctionnelle. De manière très approximative, il exprime que les espaces vectoriels normés vérifiant des conditions raisonnables du point de vue de l analyse sont des sous espaces fermés de l… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de banach-steinhaus