- Theoreme de Minkowski
-
Théorème de Minkowski
En mathématiques, le théorème de Minkowski est un résultat concernant la géométrie des réseaux. Il relie le nombre de points du réseau contenu dans une partie convexe symétrique au volume fondamental du réseau.
Ce théorème est utilisé en théorie algébrique des nombres. Si K est un corps de nombres, c'est-à-dire une extension finie du corps Q des nombres rationnels, un anneau d'entiers algébriques de K est isomorphe à un réseau. Le caractère éminemment géométrique d'un réseau offre des techniques de démonstrations, utilisées par exemple pour établir le fait que le groupe des classes d'idéaux est fini, ou encore pour déterminer la structure du groupe des unités de l'anneau.
Ce résultat a été découvert par Hermann Minkowski en 1891[1] et publié en 1896 dans son livre de Géométrie des nombres[2].
Sommaire
Énoncés
Première formulation — Soit d un entier strictement positif et C un convexe de Rd, symétrique par rapport à l'origine et de volume strictement supérieur à 2d. Le convexe C contient au moins deux points à coordonnées entières et différent du vecteur nul.
Il est posible d'exprimer ce résultat en termes de réseau.
Formulation en termes de réseau — Soit d un entier strictement positif, Λ un réseau de Rd de volume fondamental V' et C un convexe symétrique par rapport à l'origine de volume strictement supérieur à 2d.V. Le convexe C contient au moins deux points non nuls du réseau.
Cas où C est fermé — Avec les mêmes hypothèses que celle du théorème précédent, si C est fermé et de volume égal à 2d.V, le convexe C contient encore au moins deux points non nuls du réseau.
Interprétation géométrique
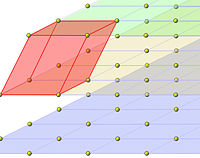
Article détaillé : Réseau (géométrie).
Exemple de réseau dans R3.
Exemple de convexe traité par le théorème de Minkowski.Un réseau est un groupe groupe additif de Rd discret, Une telle structure est nécessairement un Z module admettant une base B. Pour s'en convaincre il suffit d'étudier les propriétés d'un groupe abélien de type fini. Un Z module est un quasi espace vectoriel. Les scalaires sont munis d'une structure d'anneau et non de corps. Par définition d'un réseau, la base est de cardinal d et est aussi une base de Rd en tant qu'espace vectoriel sur R. Le réseau est composé des points dont les coordonnées dans la base B sont entières. On obtient un maillage régulier de l'espace, à l'image de la figure de gauche. Les points du réseau sont représentés par les petites billes. Un exemple de réseau est formé des points à coordonnées entières dans la base canonique de Rd. Le premier énoncé est ainsi un cas particulier du deuxième.
Un domaine fondamental est constitué des points dont les coordonnées dans la base B sont dans l'intervalle [0, 1[, le volume fondamental est le volume du domaine fondamental. Dans l'exemple précédent, il est égal à 1. Il est illustré sur la figure de gauche en rouge. Un domaine fondamental est toujours un parallélépipède.
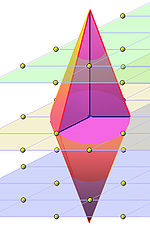
Dire que le convexe C est symétrique par rapport à l'origine signifie que si le vecteur α est élément du convexe, alors -α est aussi élément du convexe. La figure de droite représente un tel ensemble, si le point bleu représente l'origine. Il ne contient aucun autre point du réseau que l'origine, le théorème affirme que son volume est inférieur à 23 soit 8 fois le volume fondamental. En effet, dans l'exemple d est égal à 3, .
La forme du convexe donné en exemple n'est pas le fruit du hasard, on la trouve en théorie algébrique des nombres. Elle correspond à une boule pour une métrique choisie dans le cas d'un anneau d'entiers algébriques de degré 3 ayant un plongement réel et deux imaginaires (cf groupe des classes d'idéaux). Une démonstration clé utilise le théorème un théorème connexe sur un convexe de cette forme.
Démonstrations
Remarques liminaires
La valeur 2d.V est bien la plus petite possible pour que le théorème soit vrai.
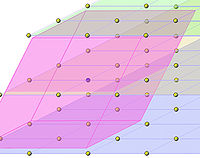
Il est possible de remplir l'espace de volumes homothétiques d'un rapport 2-d à C et centrés sur les points du réseau. L'intersection de deux volumes quelconques est vide.On peut remarquer dans un premier temps que la valeur 2d.V est bien la plus petite possible. En effet, si ε est un nombre réel strictement positif, choisi aussi petit que souhaité, l'ensemble des vecteurs de coordonnées dans la base B, comprises entre 1 - ε et 1 + ε, ne contient que l'origine comme point du réseau. Le volume de ce convexe est aussi proche que souhaité de 2d.V. Cette situation est illustrée sur la figure de gauche, le point bleu représente l'origine.
Démontrons le lemme suivant :
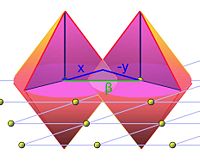
Lemme — Soit C1 l'image du convexe par l'homothétie de rapport 1/2 et α et β deux vecteurs distincts du réseau. Si C ne contient que l'origine comme point du réseau, α + C1 et β + C1 ont une intersection nulle.
Ce lemme indique que, quitte à réduire le volume de C d'un rapport 2-d, il est possible de remplir l'espace de volumes de type α + C1, où α décrit le réseau. Les intersections deux à deux, des différents volumes sont nulles. Cette propriété est à l'origine de la démonstration.
On raisonne par contraposée et l'on suppose qu'il existe deux points distincts du réseau α et β tels que α + C1 et β + C1 aient un point d'intersection. Quitte à translater par -α, on peut toujours supposer α nul. Il existe deux points x et -y de C1, tels que x = β - y. Ce qui est illustré sur la figure de droite. On en déduit que x + y est égal à β. Comme C1 est stable par symétrie par rapport à l'origine, y est un élément de C, et comme C1 est un convexe, 1/2(x + y) est aussi élément de C1. Ce qui montre que 1/2.β est élément de C1 ou encore que β est élément de C. Donc, si l'intersection de α + C1 et β + C1 est non vide, C contient un point non nul du réseau et même deux, car son inverse est aussi élément de C. La contraposée démontre bien la proposition recherchée.
Preuve
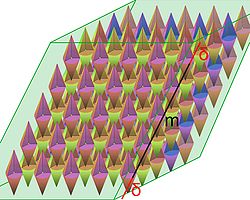Le principe de la démonstration consiste à remplir un hypercube de translatés de convexes C1.On suppose dans un premier temps que C est borné. On raisonne encore par contraposée, c'est-à-dire que l'on suppose que C ne contient aucun autre point du réseau que l'origine et l'on montre que le volume S de C est plus petit que 2d.V. Pour cela, on considère un entier m strictement supérieur à 0 et Am l'ensemble des points du réseau dont les coordonnées dans la base B sont positives et strictement plus petites que m. À chaque point α de Am on associe le convexe α + C1 et Bm est l'union de tous ces convexes, si α parcourt Am. On obtient un volume composé d'une pluralité de convexes translatés de C1 comme illustré sur la figure de gauche.
Le lemme précédent montre le volume de Bm est égal au nombre de convexes que multiplie le volume de chacun d'eux, car l'intersection de deux convexes distincts de Bm est vide. Il existe md convexes et chacun possède un volume égal à (1/2)dS car l'homothétie de rapport 1/2 dans un espace de dimension d divise le volume par un facteur 2d.
Soit δ une borne de C1, l'ensemble Bm est inclus dans l'image par l'homothétie de rapport m + 2.δ du volume fondamental. Ce qui donne la majoration suivante :
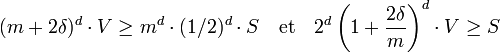
Comme m peut être choisi arbitrairement grand, un passage à la limite montre le résultat voulu.
Si C n'est pas borné, on applique le même raisonnement sur l'intersection de C et de la boule de centre 0 et de rayon n, où n est un entier positif quelconque. Chacune de ces intersections admet un volume inférieur à 2d.V. Un nouveau passage à la limite montre que C est aussi de volume inférieur à 2d.V. Comme tout convexe d'intérieur non vide et de volume bornée est borné, ce cas ne peut pas se produire.[3]
Cas du convexe fermé
On suppose ici que C est un convexe fermé de volume exactement égal à 2d.V. Dans ce paragraphe, Cn, où n est un entier strictement positif, désigne l'image de C par une homothétie de rapport 1 + 1/n. Le paragraphe précédent montre l'existence d'un point αn non nul du réseau élément de Cn. La suite (αn) est à valeur dans le compact intersection de C1 et des points non nuls du réseau, il existe une sous-suite convergente et la limite α est un point non nul du réseau.
Cette limite est élément de la suite des compacts emboités Cn et fait partie de l'adhérence de C. Comme C est fermé, α est élément de C, ce qui termine la démonstration.
Démonstration alternative
La géométrie de l'espace Rd quotienté par le réseau est un tore de dimension d.
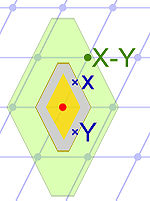
La géométrie de l'espace Rd quotienté par le réseau est un tore de dimension d.Il existe une manière élégante de démontrer le théorème, à l'aide d'un groupe topologique. L'espace Rd peut être vu comme un groupe et le réseau un sous-groupe. Quotienter l'espace par le réseau revient à identifier chaque élément de Rd avec un élément du domaine fondamental. En dimension 2, cela revient à coller les points du domaine fondamental de première coordonnée égale à 1 avec ceux dont la première coordonnée est égale à 0 et agir de même avec la deuxième coordonnée. On obtient un tore de dimension d, illustré en dimension 2 par la figure de gauche. Pour chaque point du tore, il existe un voisinage et un difféomorphisme d'un voisinage de Rd vers ce voisinage. Ces difféomorphismes permettent de définir une mesure sur le tore, tel que tout espace mesurable du domaine fondamental soit mesurable sur le tore et de même mesure. La mesure du tore est celle du volume fondamental V.
Cette mesure est l'outil de la démonstration alternative. La démonstration est cette fois-ci directe. On suppose que le convexe C, illustré en vert dans l'exemple de droite, est de mesure strictement supérieure à 2d.V. Son image C1, illustré en jaune, par l'homothétie de rapport 1/2, est de mesure strictement supérieure à V égal au volume fondamental. L'image de C1 par le morphisme canonique de groupe, définissant le tore, ne peut être injective car la mesure de l'image serait supérieure à celle du tore tout entier. Il existe donc deux éléments de C1, x et y ayant même image par le morphisme canonique.
La zone de non injectivité est illustrée en gris sur la figure de droite. Dans l'exemple, certains points du tore sont touchés deux fois, la zone est représentée en gris et d'autres une unique fois, représenté en jaune, sur la figure de gauche. La zone grise est composée de deux bandes dont l'une fait le tour d'une section horizontale et l'autre d'une section verticale. Le point x - y est élément non nul du réseau car x et y sont deux représentants différents d'une même classe. Il est aussi élément de C car la convexité et la stabilité par symétrie autour de l'origine de C1 montre que 1/2(x - y) est élément du convexe.[4]
Applications
Ce théorème est habituellement utilisé pour démontrer deux résultats importants en théorie algébrique des nombres : le théorème des unités de Dirichlet, et la finitude du groupe des classes.
Voir aussi
Notes
- ↑ Jiri Matousek, Lectures on Discrete Geometry [détail des éditions], p. 20
- ↑ Hermann Minkowski, Geometrie der Zahlen, Teubner, Leipzig, 1896 ; republié par Johnson, New York, 1968
- ↑ La preuve présenté ici est très classique, on la trouve par exemple sur :proof of Minkowski's theorem par Planetmath.org
- ↑ On trouve cette démonstration, par exemple dans la référence : B. Edixhoven Théorie algébrique des nombres de l'Université de Renne I. p 33
Liens externes
- (fr) V et F Bayart Théorème de Minkowski La bibmath
- (fr) P. Q. La géométrie des nombres École Normale Supérieure, Université Denis Diderot
- (en) Alozano Minkowski's theorem Planetmath.org
Bibliographie
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
- Jiri Matousek, Lectures on Discrete Geometry [détail des éditions]
Portail des mathématiques
Catégories : Géométrie convexe | Réseau (mathématiques) | Théorie algébrique des nombres | Théorème de mathématiques
Wikimedia Foundation. 2010.
