Extension De Corps

En mathématiques, plus particulièrement en algèbre, l'extension d'un corps K est un corps L qui contient K comme sous-corps.

Par exemple, , le corps des nombres complexes, est une extension de , le corps des nombres réels, lequel est lui-même un extension de , le corps des nombres rationnels.

On note parfois L / K pour indiquer que L est une extension de K.

Sommaire 1 Définition 2 Degré d'une extension 3 Extension algébrique, extension transcendante 4 Extension simple 5 Extension de Galois

Définition

Soit K un corps. Une extension de K est un couple (L, j) où L est un corps et j un morphisme de corps de K dans L (les morphismes de corps étant systématiquement injectifs).

On montre qu'il existe un sur-corps N de K et un isomorphisme de corps 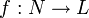tels que la restriction de f à K soit égale à j. Ainsi l'extension (L, j) peut être identifiée à l'extension (N, i) avec l'inclusion i. Pour cette raison, les extensions d'un corps sont généralement considérées comme des sur-corps.

Une sous-extension de L / K est un sous-corps de L contenant K. Si V est un sous-ensemble de L, alors on définit le corps K(V) comme le plus petit sous-corps de L contenant K et V. Il est constitué des éléments de L pouvant être obtenus grâce à un nombre fini d'opérations additives et multiplicatives, et d'inversions sur K et V. Si L = K(V), on dit que L est engendré par V.

Degré d'une extension

Soit L / K une extension de corps. L peut être considéré comme un espace vectoriel sur K, où l'addition vectorielle est l'addition sur L et la multiplication scalaire est la restriction de la multiplication à K.

La dimension de cet espace vectoriel est appelée le degré de l'extension et est notée . L'extension est dite « finie » ou « infinie » selon que le degré est fini ou non. Par exemple, et l'extension 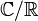est donc finie. Par contre, , le cardinal du continu, et l'extension 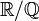est donc infinie.

Si M est une extension finie de L qui est elle-même une extension finie de K, alors M est une extension finie de K et on a .

Extension algébrique, extension transcendante

Si L est une extension de K, alors un élément de L qui est une racine d'un polynôme non-nul sur K est dit algébrique sur K. Dans le cas contraire, l'élément est dit transcendant sur K. Dans le cas où 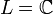et 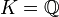, on parle de nombre algébrique et de nombre transcendant.

Si tout élément de L est algébrique sur K, l'extension L / K est dite algébrique. Dans le cas contraire, elle est dite transcendante. Par exemple, toute extension finie est algébrique, et on peut montrer qu'une extension est algébrique si et seulement si elle est l'union de ses sous-extensions finies.

Par exemple, 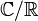, finie, est algébrique, mais 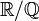est transcendante.

Si L est engendré par une famille d'éléments algébriquement indépendants sur K, l'extension est dite purement transcendante.

Toute extension est extension algébrique d'une extension purement transcendante.

Une extension L/K engendrée par une famille finie V est dite de type fini. Toute extension finie est de type fini. L'extension 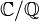n'est pas de type fini. Si L/K est de type fini, alors L est une extension finie d'un corps de fractions rationnelles K(X₁,...,X_n) à plusieurs variables. Les extensions de type fini interviennent en Géométrie algébrique, ce sont exactement les corps de fonctions rationnelles sur les variétés algébriques intègres.

Extension simple

Si L / K est une extension de corps et V est un sous-ensemble de L, alors on définit le corps K(V) comme le plus petit sous-corps de L contenant K et V. Il est constitué des éléments de L pouvant être obtenus grâce à un nombre fini d'opérations additives et multiplicatives, et d'inversions sur K et V. Si L = K(V), on dit que L est engendré par V.

Une extension de corps engendrée par un seul élément est appelée extension simple. Une telle extension est de degré fini si elle est engendrée par un élément algébrique et purement transcendante si elle est engendrée par un élément transcendant.

Par exemple, est une extension simple de car elle est engendrée par i, l'unité imaginaire. L'extension 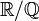, n'étant ni finie, ni purement transcendante, n'est pas simple.

Extension de Galois

Une extension finie L/K est dite de Galois ou galoisienne si elle est normale et séparable. Le groupe des automorphismes de l'extension est fini, d'ordre le degré de l'extension [L : K]. Ce groupe est appelé groupe de Galois de l'extension.

Par exemple, 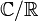est de Galois, son groupe de Galois est le groupe cyclique d'ordre 2.

Articles de mathématiques en rapport avec la théorie de Galois
Corps	Corps fini · Corps parfait · Corps de rupture · Corps de décomposition
Extension de corps	Extension algébrique · Extension quadratique · Extension simple · Extension normale · Extension séparable · Extension de Galois · Groupe de Galois · Clôture algébrique
Articles associés	Caractéristique · Polynôme formel · Polynôme cyclotomique · Théorie de Galois · Théorème fondamental de la théorie de Galois · Théorème de l'élément primitif · Théorie d'Iwasawa

• Portail des mathématiques