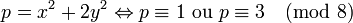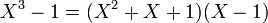- Nombres premiers somme de 2 carrés
-
Théorème des deux carrés de Fermat
En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c'est-à-dire de deux carrés d’entiers) et précise de combien de façons différentes il peut l’être. Par exemple, selon ce théorème, un nombre premier impair est une somme de deux carrés parfaits si et seulement si le reste de sa division euclidienne par 4 est 1 ; dans ce cas, les carrés sont déterminés de manière unique. On peut le vérifier sur 17 (= 4x4 + 1) ou 97 (= 24x4 + 1), qui sont bien tous deux d’une seule façon une somme de deux carrés (17 =1²+4² et 97 = 9²+4²), alors que des nombres premiers comme 7 (=4x1+3) ou 31 (4x7+3) ne sont pas des sommes de deux carrés. Ce résultat est parfois nommé simplement théorème des deux carrés ou bien encore théorème de Fermat de Noël.
Il s’inscrit dans la longue histoire de la représentation de nombres comme sommes de carrés qui remonte à l’Antiquité. Il est explicité par Pierre de Fermat (1601-1665) au XVIIe siècle, mais la première preuve publiée connue est l'œuvre de Leonhard Euler un siècle plus tard. Sa démonstration ne clôt pas les interrogations. Des nouvelles preuves et diverses généralisations sont proposées au cours des siècles suivants. Elles ont joué un rôle important dans le développement d’une branche des mathématiques appelée théorie algébrique des nombres.
À l'instar de beaucoup d'équations diophantiennes, c’est-à-dire d’équations dont les coefficients et les solutions cherchées sont des nombres entiers ou fractionnaires, la simplicité de l'énoncé cache une difficulté réelle de démonstration. Certaines des preuves proposées ont aidé à la mise au point d'outils parfois sophistiqués, comme les courbes elliptiques ou la géométrie des nombres, liant ainsi la théorie des nombres élémentaire à d’autres branches des mathématiques.
Sommaire
Présentation du théorème
Le cas des nombres premiers
Certains nombres premiers sont sommes de deux carrés parfaits. C’est bien sûr le cas de 2 (=12 + 12), de même, 5 est la somme de 1 et de 4. D'autres comme 3 ou 7 ne vérifient pas cette propriété. Un test systématique jusqu'à 40 montre que :

En revanche, 3, 7, 11, 19, 23 et 31 ne se décomposent pas ainsi. Le théorème fournit un critère général permettant de discriminer ces deux situations :
Théorème des deux carrés de Fermat (cas des nombres premiers) — Soit p un nombre premier impair, p est somme de deux carrés d'entiers naturels si et seulement si p est congru à 1 modulo 4 :
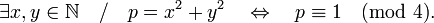
De plus, cette décomposition, quand elle existe, est unique, à l’échange près de x2 et y2.
Dire que "p est congru à 1 modulo 4" signifie simplement que le reste de la division euclidienne de p par 4 est 1, ou encore que le nombre p est de la forme 4k+1. Ce vocabulaire est explicité dans l'article Congruence sur les entiers.
Le cas général
Si, dans un premier temps, les entiers inférieurs à 50 sont écrits sur quatre lignes, en fonction du reste de leur division par quatre, on obtient :
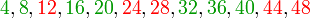
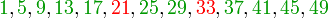
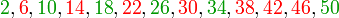
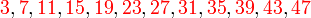
Les entiers notés en vert désignent ceux qui s'écrivent sous forme de deux carrés parfaits, les autres sont notés en rouge. On constate que la quatrième ligne ne contient pas de solution. Or le produit d'un nombre pair de facteurs de la forme 4k+3 est de la forme 4k+1, donc cette dernière ligne ne contient que des nombres qui ont un nombre impair de facteurs premiers de la forme 4k+3. Ceci donne une piste pour comprendre la situation générale.
Le cas d'un nombre n quelconque dépend de ses facteurs premiers. On a :
Théorème des deux carrés (cas général) — Un entier est somme de deux carrés si et seulement si chacun de ses facteurs premiers de la forme 4k + 3 intervient à une puissance paire.
Ainsi 30 n’est pas somme de carrés, car 30 = 2.3.5, 3 intervient avec un exposant 1 dans sa factorisation en facteurs premiers. En revanche, 45 = 32.5 est somme de carrés, car 3 intervient à la puissance 2 (on trouve bien que 45 = 62 + 32).
La question du nombre de couples de carrés dont la somme est égale à un entier n donné, est aussi plus difficile, ce nombre dépend des exposants des facteurs de n de la forme 4k+1. En écrivant
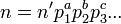 , où n' est divisible seulement par 2 et des facteurs premiers de la forme 4k+3, et où les différents pi sont les facteurs premiers de la forme 4k+1, alors n a 1/2(a+1)(b+1)(c+1)... décompositions différentes en somme de deux carrés si un au moins des exposants a, b, c, ... est impair et 1/2(a+1)(b+1)(c+1)...+1/2 décompositions si tous les exposants sont pairs.
, où n' est divisible seulement par 2 et des facteurs premiers de la forme 4k+3, et où les différents pi sont les facteurs premiers de la forme 4k+1, alors n a 1/2(a+1)(b+1)(c+1)... décompositions différentes en somme de deux carrés si un au moins des exposants a, b, c, ... est impair et 1/2(a+1)(b+1)(c+1)...+1/2 décompositions si tous les exposants sont pairs.Une autre expression équivalente de ce nombre de décompositions a été donnée par Charles Gustave Jacob Jacobi (1804-1851) :
Théorème des deux carrés (compléments) — Soit n un entier
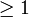 et r2(n) le nombre de représentations de n comme somme de deux carrés. Soit d1 (resp. d3) le nombre de diviseurs (pas nécessairement premiers) de n congrus à 1 (resp. 3) modulo 4, la formule suivante est vérifiée :
et r2(n) le nombre de représentations de n comme somme de deux carrés. Soit d1 (resp. d3) le nombre de diviseurs (pas nécessairement premiers) de n congrus à 1 (resp. 3) modulo 4, la formule suivante est vérifiée :r2(n) = 4(d1(n) − d3(n)). On compte toutes les représentations, même celles qui ne diffèrent que par le signe ou l'ordre. Par exemple,
 admet 8 représentations comme somme de deux carrés. On trouve cet énoncé et une preuve dans Introduction à la théorie des nombres de Hardy & Wright, théorème 278.
admet 8 représentations comme somme de deux carrés. On trouve cet énoncé et une preuve dans Introduction à la théorie des nombres de Hardy & Wright, théorème 278.Un dernier aspect important est la construction explicite des carrés dont la somme est égale à un entier n donné.
Histoire
Antiquité : premiers résultats
L'intérêt pour les sommes de carrés remonte à l’Antiquité : on trouve de telles sommes dans des tablettes en cunéiforme du début du 2e millénaire avant notre ère et deux lemmes ajoutés au théorème X. 28 dans les Éléments d'Euclide expliquent comment construire des carrés parfaits sont la somme ou la différence forment encore des carrés parfaits, ou au contraire comment ne pas obtenir un carré en sommant deux carrés[1].
Mais c’est dans la tradition diophantienne que l’on trouve des traces plus précises sur les nombres sommes de carrés. Les Arithmetica[2], composées à une date incertaine, contiennent des problèmes dont les solutions cherchées sont rationnelles ou entières. Un grand nombre d’entre eux concerne les nombres carrés ou cubiques (en l’occurrence des carrés ou des cubes de nombres rationnels). À titre d'exemples, le problème 11 du livre II est le suivant : « Ajouter un même nombre à deux nombres donnés de manière que chacun d'eux forme un carré », ou encore le problème 22 du livre IV : « Trouver trois nombres tels que le nombre solide issu de ces nombres [autrement dit, le produit de ces trois nombres], augmenté de chacun d’eux, forme un carré.[3] ». Pour résoudre toutes ces questions, Diophante introduit une « quantité indéterminée d’unités » qu’il appelle « arithme » et exprime en fonction d’elle toutes les données du problème (c’est donc un ancêtre de la notion d’inconnue en algèbre). Il arrive ainsi à trouver une solution numérique particulière, par exemple pour le problème II.11 la solution 97/64 si les nombres donnés sont 2 et 3, et pour le problème IV.22, la solution 1, 34/6 et (2.1/2)/6.
Plusieurs mentions pertinentes pour la détermination des nombres sommes de deux carrés apparaissent de manière dispersée dans divers problèmes. Par exemple, Diophante note sans explication que 15 ne peut être la somme de deux carrés de nombres rationnels au milieu de la solution du problème VI.14. Dans le livre III, il affirme que le nombre 65 est une somme de deux carrés de deux façons différentes, car c'est le produit de 5 et 13, eux-mêmes sommes de deux carrés[4]. Un autre problème concerne le fait de « partager l'unité en deux parties et ajouter à chacun des fragments un nombre donné, de manière à former un carré. ». Ceci revient à chercher une expression de :
 sont des carrés de nombres rationnels. Ici :
sont des carrés de nombres rationnels. Ici : 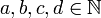
Ceci revient à chercher 2c + 1 comme somme de deux carrés. Diophante dit explicitement que c doit être pair, autrement dit que la division de 2c + 1 par 4 donne pour reste 1[5].
Certains mathématiciens lecteurs de Diophante étudieront de manière plus systématique et plus arithmétique les nombres sommes de carrés, en particulier la tradition en langue arabe de al-Khazin, al-Sizji, al-Samaw’al, etc. [6]. Leur perspective combine, sur les problèmes diophantiens qui s’y prêtent, des techniques inspirées de l’algèbre naissante et un point de vue euclidien, en particulier une focalisation sur les nombres entiers et des preuves générales. Par exemple, ils montrent qu’une somme impaire de deux carrés premiers entre eux est de la forme 12k+5 ou 12k+1. Un contexte important est l'étude des triangles rectangles en nombres, ou triplets pythagoriciens, c'est-à-dire des nombres vérifiant a2 + b2 = c2 : en effet, si les côtés a, b, c sont premiers entre eux, c lui-même s'écrit comme une somme de carrés.
XVIIe siècle : Les énoncés
 Marin Mersenne, Minime et homme de science, établit un contact épistolaire solide entre Pierre Fermat et ses contemporains.
Marin Mersenne, Minime et homme de science, établit un contact épistolaire solide entre Pierre Fermat et ses contemporains.
C'est en lien direct avec les éditions et commentaires des Arithmétiques de Diophante que l'on trouve au XVIIe siècle une exploration plus sytématique, puis les premiers énoncés complets de ce théorème.
Albert Girard achève ainsi la traduction de Simon Stevin des livres de Diophante et dans ses annotations, en 1634, annonce que les nombres s'exprimant comme somme d'au plus deux carrés sont « les carrés, les nombres premiers de la forme 4k+1, les produits de nombres de ces deux formes et le double de chacun des nombres obtenus », c'est-à-dire un énoncé équivalent à l'énoncé général donné ci-dessus[7]. Aucun élément de preuve n'est cependant apporté.
C'est à peu près à la même date que Marin Mersenne (1588-1648) met en place à Paris une académie toute mathématique communiquant les résultats des différents travaux, et appuyée sur un important réseau de correspondants à travers toute l'Europe. Y participent des noms restés plus ou moins célèbres comme Étienne et Blaise Pascal (1623 1662), René Descartes, Bernard Frénicle de Bessy (1605 1675), Gilles Personne de Roberval ou encore Pierre de Carcavi, bibliothécaire du Roi. Cette correspondance est une des deux principales sources pour les travaux arithmétiques de Pierre Fermat, l'autre étant ses propres commentaires à l'édition de Diophante qu'a donnée Claude Gaspard Bachet de Méziriac en 1621[8]. Dans ses travaux de théorie des nombres, Bachet s'inscrit dans la tradition de l'analyse diophantienne entière, il donne de nouveaux exemples numériques en entiers, et surtout des preuves à la mode euclidienne de nombreuses propositions[9]. En particulier il prouve que le produit de deux sommes de deux carrés est une somme de deux carrés, de deux façons différentes[10] ; plus précisément, en notation algébrique actuelle:
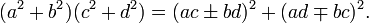
Cette identité est fondamentale pour passer du cas des nombres premiers au cas général.
Mersenne encourage ses correspondants à se proposer mutuellement des problèmes, afin d’en tester la difficulté auprès des autres mathématiciens et de les stimuler dans leurs recherches. L’un des premiers proposés à Fermat en 1636 concerne les sommes de plusieurs carrés, et dès mars 1638, Mersenne indique à Descartes que Fermat a prouvé qu’un nombre de la forme[11] 4’’k’’+3 n’est ni carré, ni somme de deux carrés (rationnels). En 1640, reprenant contact avec Roberval après une interruption de leur correspondance, Fermat lui rappelle ce résultat déjà un peu ancien et explique :
Voici ce que j’ai découvert depuis sur le sujet de la proposition 12 du cinquième Livre de Diophante [12]. Si un nombre donné est divisé par le plus grand carré qui le mesure et que le quotient se trouve mesuré par un nombre premier moindre de l’unité qu’un multiple du quaternaire, le nombre donné n’est ni carré, ni composé de deux carrés (rationnels). ... J’ai démontré ensuite ... [que s]i un nombre est composé de deux carrés premiers entre eux, je dis qu’il ne peut être divisé par aucun nombre premier moindre de l’unité qu’un multiple du quaternaire[13].
Autrement dit, en termes plus modernes, si on écrit un nombre n sous la forme
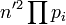 et qu'un des facteurs premiers pi est de la forme 4k-1, n n'est pas une somme de carrés, ni en entiers, ni en nombres rationnels (c'est-à-dire ne divise même pas une somme de carrés). Et si p premier divise a2 + b2, avec a et b premiers entre eux, alors p n'est pas de la forme 4k-1 (c'est donc 2 ou un premier de la forme 4k+1).
et qu'un des facteurs premiers pi est de la forme 4k-1, n n'est pas une somme de carrés, ni en entiers, ni en nombres rationnels (c'est-à-dire ne divise même pas une somme de carrés). Et si p premier divise a2 + b2, avec a et b premiers entre eux, alors p n'est pas de la forme 4k-1 (c'est donc 2 ou un premier de la forme 4k+1).Mais c’est surtout dans une longue missive à Mersenne[14] datée du jour de Noël que Fermat énonce ses fondements pour résoudre tous les problèmes liés aux sommes de carrés. Pour cette raison, le théorème est parfois appelé théorème de Fermat de Noël.
Tout nombre premier [=p], qui surpasse de l’unité un multiple du quaternaire [tel que p = 4k + 1] est une seule fois la somme de deux carrés. De même son carré [p2]. Son cube [p3] et son carré-carré [p4] sont chacun deux fois la somme de deux carrés ; son carrécube [p5] et son cubecube [p6] sont chacun trois fois la somme de deux carrés; etc., à l’infini...
Ce résultat réapparaît dans le contexte de différents problèmes, Fermat y ajoute bientôt le problème de la construction même des carrés. Le théorème sur les sommes de carrés figure aussi dans les fameuses observations que Fermat a écrit en marge de l'édition de Bachet des Arithmétiques de Diophante, observations qu'on connaît par la version posthume publiée par son fils en 1670[15].
L'interlocuteur le plus important de Fermat sur la théorie des nombres, Frenicle, manifeste d'ailleurs qu'il a trouvé aussi cet énoncé : il demande par exemple à Fermat de trouver le plus petit nombre qui soit somme de deux carrés exactement un nombre de fois donné, et consacre le 5e exemple de son propre traité La Méthode des Exclusions au problème : « un nombre étant donné, déterminer combien de fois il est la somme de deux carrés ».
Le XVIIe siècle : qu'en est-il des preuves ?
Si l'énoncé est un bien collectif pour ces mathématiciens, il n'en est pas de même de la démonstration. Éliminer les diviseurs premiers de la forme 4k-1 peut se faire en considérant simplement les restes de la division des carrés par 4 : sollicité par Mersenne, comme indiqué, Descartes délègue un de ses protégés, Jean Gillot, pour résoudre la question avec succès. Le dénombrement des solutions, une fois l'identité « de Brahmagupta » connue, est un exercice de combinatoire que plusieurs auteurs, comme Frenicle par exemple mènent aussi à bien. Reste la preuve que tout nombre premier de la forme 4k+1 est une somme de carrés parfaits. Or, il existe peu (voire pas du tout) de modèles de telles preuves d'existence dans un contexte arithmétique. L'interprétation géométrique des nombres entiers, à la base des preuves euclidiennes, est très lourde. Une solution consiste en une réinterprétation algébrique de ces problèmes : tout comme Stevin, François Viète, l'inventeur d'une des premiers symbolismes algébriques cohérents à grande échelle, a ainsi reformulé une grande partie des Arithmétiques de Diophante à la fin du XVIe siècle. Mais, géométrie ou algèbre, comment garder trace du fait qu'on cherche ici des solutions entières ? Fermat est tout particulièrement conscient de cette difficulté : dans un défi mathématique aux mathématiciens d' Europe, en 1657, il déclare : « À peine trouve-t-on qui pose des problèmes purement arithmétiques, ni qui les comprenne. N'est ce pas parce que jusqu'ici l'arithmétique a été traité géométriquement plutôt qu'arithmétiquement[16] ? »
C'est dans le but de développer cette analyse diophantienne entière, avec des preuves, que Fermat a mis au point une méthode, celle qu'il nomme la descente infinie[17] et qui, d'après ses dires, lui permet d'en venir à bout :
Je fus longtemps sans pouvoir appliquer ma méthode aux questions affirmatives, parce que le tour et le biais pour y venir est beaucoup plus malaisé que celui dont je me sers aux négatives. De sorte que, lorsqu'il me fallut démontrer que tout nombre premier, qui surpasse de l'unité un multiple de 4, est composé de deux quarrés, je me trouvai en belle peine. Mais enfin une méditation diverses fois réitérée me donna les lumières qui me manquoient, et les questions affirmatives passèrent par ma méthode, à l'aide de quelques nouveaux principes qu'il y fallut joindre par nécessité.[18]
Fermat avait-il d'une démonstration complète de son théorème ? Aucune preuve rédigée par lui de ce théorème n'a subsisté. En revanche, les ingrédients qu'il a mis au point (petit théorème de Fermat, descente infinie) permettent effectivement d'en fabriquer une et plusieurs historiens se sont livrés à cet exercice de reconstruction[19].
Comme quelques autres, les premiers cas de son Grand Théorème en particulier, l'énoncé sur les sommes de deux carrés occupe en tout cas une place centrale dans le programme de Fermat pour rénover la théorie des nombres. Quatorze ans plus tard, bien après la mort de Mersenne, on voit réapparaître ces énoncés dans un projet d'ouvrage que Fermat adresse à Blaise Pascal, puis en 1658 au cours d'un échange avec les mathématiciens anglais, John Wallis et William Brouncker, et un an plus tard, dans un bilan sur la théorie des nombres destinée au jeune Christiaan Huygens. Fermat remarque aussi que des lois analogues peuvent être trouvées pour les nombres premiers x2 + 2.y2 = p et x2 + 3.y2 = p[20].
XVIIIe siècle : Preuves et extensions
 Leonhard Euler rédige la première preuve connue.
Leonhard Euler rédige la première preuve connue.
L'environnement scientifique du siècle suivant est bien différent. Les mathématiques se sont professionnalisées partout en Europe et des journaux réguliers, en particulier les publications des diverses Académies des sciences, offrent la possibilité de publier au fur et à mesure résultats et preuves. Leonhard Euler (1707-1783) s'est intéressé au théorème des deux carrés, comme à beaucoup d'autres résultats de théorie des nombres laissés par Fermat[21], et on lui doit les premières preuves connues de ces énoncés.
La référence géométrique à des triangles rectangles de côtés entiers disparait complètement au profit d'un formalisme purement algébrique. Euler étudie en particulier, à côté d'autres équations diophantiennes, les trois familles d'équations suivantes :
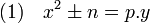

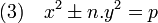
 Joseph-Louis Lagrange développe un outil essentiel pour généraliser le résultat : les formes quadratiques.
Joseph-Louis Lagrange développe un outil essentiel pour généraliser le résultat : les formes quadratiques.
Ici, n désigne un nombre entier strictement positif et p un nombre premier. La dernière équation généralise celle associée au théorème des deux carrés (cas où n est égal à un).
En ce qui concerne le théorème des deux carrés, Euler montre d'abord qu'un nombre premier p = 4n − 1 ne divise pas une somme de deux carrés premiers entre eux, a2 + b2, en appliquant le petit théorème de Fermat. Il montre aussi qu'un diviseur d'une somme de deux carrés a2 + b2 est encore de cette forme (et donc s'il est premier, c'est soit 2 soit un entier de la forme 4n+1) ; ce résultat s'étend au cas de n=2 ou 3 (on trouve qu'un diviseur impair premier est congru à 1 ou 3 modulo 8 pour n=2 et à 1 modulo 3 pour n=3); dans ces derniers cas, la preuve inverse repose aussi sur des identités de puissances n-ièmes et le petit théorème de Fermat.
On trouve trace de ces résultats au fil de sa correspondance avec Christian Goldbach[22] (qui contribue lui-même à cette étude), dès le début des années 1740, avec des publications détaillées, dans les Mémoires de l'Académie de Saint-Pétersbourg en particulier, une décennie plus tard[23]. André Weil évoque cette période comme une « campagne de sept années » pour prouver toutes les assertions de Fermat sur les sommes de deux carrés ; jusque dans les années 1770, Euler y revient encore pour donner des variantes de ses preuves et de ces résultats.
Euler accumule aussi toutes sortes d'expérimentations numériques. Il conjecture dans ce contexte un résultat appelé à devenir une des lois centrales de la théorie des nombres, la loi de réciprocité quadratique, sans pouvoir le démontrer[24].
Reprenant une suggestion de Fermat, il interprète aussi le théorème sur les sommes de carrés comme un test de primalité[25]. En effet, un nombre de la forme 4n + 1 est premier si et seulement s'il s'écrit d'une seule façon comme somme de deux carrés, et que ces carrés sont premiers entre eux. Ce critère permet à Euler de montrer que le 5e nombre de Fermat,
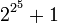 , n'est pas premier car il s'écrit de deux manières comme somme de carrés :
, n'est pas premier car il s'écrit de deux manières comme somme de carrés :(216)2 + 12 = 622642 + 204492. Euler cherche également à déterminer pour quels entiers μ,ν, l'étude des nombres représentables sous la forme μx2 + νy2 lui fournirait encore un critère de primalité analogue. Avec l'aide de ses assistants, il trouve que le critère marche lorsque le produit μν fait partie d'une liste de 65 nombres, qu'il baptise numeri idonei, nombres idoines[26]. En utilisant le plus grand de ces nombres, 1848, Euler montre par exemple que 18518809( = 1972 + 180480000) est premier.
Joseph-Louis Lagrange (1736-1813) intègre les résultats tant théoriques que numériques d'Euler et les étend, dans un long mémoire en deux parties, intitulé « Recherches d'arithmétique »[27]. Lagrange ne se limite pas à l'étude des nombres représentés par des sommes de carrés, mais étudie plus généralement les nombres entiers qui peuvent s'écrire sous la forme ax2 + bxy + cy2, pour des entiers x,y à trouver, les entiers a,b,c étant fixés. Une telle expression est appelée une forme quadratique[28] binaire (c'est-à-dire du deuxième degré et à deux variables). Le théorème des deux carrés concerne la forme quadratique x2 + y2, c'est-à-dire celle pour laquelle a = c = 1,b = 0. Lagrange montre en particulier que deux formes f(x,y) et F(X,Y)représentent les mêmes entiers si un changement de variables x = αX + βY,y = γX + δY (avec des coefficients α,β,γ,δ entiers et tels que[29]
 ) transforme l'une en l'autre, et que pour deux formes ainsi reliées, la quantité b2 − 4ac, le discriminant de la forme, est identique. De telles formes seront appelées « équivalentes » par Gauss quelques décennies plus tard et l'exploration de cette relation entre formes quadratiques par Lagrange constitue l'une des premières études connues d'une relation d'équivalence. Pour un discriminant donné, il n'y a qu'un nombre fini de classes de formes, à équivalence près[30].
) transforme l'une en l'autre, et que pour deux formes ainsi reliées, la quantité b2 − 4ac, le discriminant de la forme, est identique. De telles formes seront appelées « équivalentes » par Gauss quelques décennies plus tard et l'exploration de cette relation entre formes quadratiques par Lagrange constitue l'une des premières études connues d'une relation d'équivalence. Pour un discriminant donné, il n'y a qu'un nombre fini de classes de formes, à équivalence près[30].Lagrange remarque que les deux nombres entiers a et c sont représentés de manière primitive, c'est-à-dire avec des entiers x,y premiers entre eux par la forme quadratique ax2 + bxy + cy2 (puisque a = f(1,0),c = f(0,1), et aussi par toute forme équivalente ; réciproquement, il établit que tout nombre entier représentable de manière primitive par une forme est le coefficient du terme en X2 pour une autre forme équivalente à la première, et que tout diviseur d'une forme est représentable par une forme de même discriminant (pas nécessairement équivalente). En particulier, si un nombre premier p divise la valeur en des entiers d'une forme quadratique, le discriminant D de la forme est un carré modulo p. La loi de réciprocité permet d'exprimer à l'inverse cette condition comme l'appartenance de p à certaines classes de congruence modulo la valeur absolue du discriminant (généralisant le fait que p doit être congru à 1 modulo 4 pour être représenté par une somme de carrés, c'est-à-dire une forme quadratique de discriminant -4).
Lagrange montre enfin comment, dans chaque classe de formes équivalentes, trouver des formes représentantes particulièrement simples : pour un discriminant négatif, il peut définir une forme représentante unique (dite forme réduite) par classe, pour un discriminant positif, la caractérisation des formes réduites fait appel à son étude sur l'équation (2) ci-dessus et aux fractions continues[31].
Adrien-Marie Legendre (1752-1833) apporte sa pierre à l'édifice. Avant la fin du siècle, il introduit un symbole portant maintenant son nom permettant d'exprimer plus simplement la loi de réciprocité quadratique, même si la démonstration complète de cette loi lui échappe encore[32].
XIXe siècle : nouveaux outils et nouveaux cadres
 Carl Friedrich Gauss propose une nouvelle preuve et développe plusieurs outils connexes au théorème.
Carl Friedrich Gauss propose une nouvelle preuve et développe plusieurs outils connexes au théorème.
Au cours du XIXe siècle, l'étude des problèmes sur les nombres entiers change de statut. D'une part, elle donne lieu à de vastes synthèses théoriques, unifiant de nombreuses questions jusqu'alors éparses. D'autre part, de marginale qu'elle était dans l'ensemble des mathématiques, elle devient l'objet de nombreuses interactions avec d'autres branches, comme la géométrie ou l'analyse réelle ou complexe[33]. Le théorème des deux carrés bénéficie de ce double changement : il est intégré dans de nouveaux cadres, utilisé parfois comme une illustration des propriétés plus ou moins profondes mises à jour, et il est démontré plus directement, ou affiné, grâce à l'emploi de méthodes géométriques ou analytiques.
En 1801, Carl Friedrich Gauss (1777-1855) publie un livre d'arithmétique[34] novateur. La logique suivie consiste à étudier les nombres à l'aide d'une démarche structurelle. Il découvre que de multiple configurations, maintenant dénommées anneau euclidien bénéficiant des mêmes propriétés et donc d'une arithmétique analogue. Elle est parfois appelée arithmétique de l'horloge. De nouveaux ensembles de nombres sont étudiés, parfois de cardinal fini, parfois généralisant les entiers. Ces résultats offrent des démonstrations plus simples du théorème des deux carrés[35], permettent de prouver la loi de réciprocité quadratique[36] et étendent la classification des formes quadratiques de Lagrange[37].
Les travaux de Gauss influencent les mathématiciens du siècle, Jacobi les utilisent pour établir une démonstration du nombre exact de décompositions d'un entier en deux carrés[38]. Richard Dedekind (1831-1916), le dernier en date des élèves de Gauss, propose deux preuves à la fois élégantes et concises à l'aide des entiers de Gauss. Celle présentée dans cet article est la seconde[39].
Si les idées de Gauss permettent de mieux comprendre les nombres, le cas général reste hors de portée. Pour y arriver, il faudrait être capable de classifier toutes les formes quadratiques et les avancées du mathématicien sont insuffisantes. Cette classification suppose la connaissance des structures des extensions d'entiers, appelées entiers algébriques. Si ces ensembles disposent toujours d'une addition et d'une multiplication conférant une structure d'anneau, plus la valeur n augmente plus elle devient complexe. La division euclidienne disparait, puis, fait encore plus gênant, le théorème fondamental de l'arithmétique garantissant l'unicité de la décomposition en facteurs premiers s'évanouit à son tour.
Johann Peter Gustav Lejeune Dirichlet (1805-1859) élucide la structure des éléments inversibles, Ernst Kummer (1810-1893) trouve comment remplacer les facteurs premiers manquant à l'aide d'une notion maintenant appelé idéal, Evariste Galois (1811-1832) ébauche une vaste théorie permettant de mieux comprendre comment les nombres se multiplient. Chacun des progrès, conséquence de l'œuvre de ses différents savants, permet de résoudre quelques cas supplémentaires[40]. Le cas général n'est finalement résolu qu'à la dernière année du siècle grâce à la touche finale[41] de David Hilbert (1862-1943).
Démonstrations
Les différentes démonstrations sont regroupées en fonctions des époques et des auteurs. En revanche, la rédaction choisie utilise le formalisme moderne : ainsi, la présentation des résultats de Diophante est très éloignée de la forme géométrique présente dans les textes originaux. Les preuves ont été choisies pour leur simplicité. En conséquence, la démonstration fondée sur les entiers de Gauss est due à Dedekind, celle utilisant les résultats de Lagrange sur les formes quadratiques est due à Gauss et certains résultats de Fermat sont exprimés en termes de résidus, vocable contemporain qui n'apparait qu'à la fin du XVIIIe siècle.
Époque de Diophante
Une première approche élémentaire montre que :
-
- Si un entier n est somme de deux carrés, alors le reste de la division de n par 4 n'est jamais égal à 3.
Elle se démontre en étudiant les restes de la division euclidienne par 4 d'un carré parfait.
Une identité remarquable, souvent dénommée identité de Brahmagupta permet d'établir le résultat suivant :
-
- Si deux entiers n et m sont sommes de deux carrés, alors leur produit est aussi somme de deux carrés.
Les deux entiers n et m peuvent être vus comme le carré du module de deux nombres complexes à parties réelle et imaginaire entières. Comme le produit de deux modules est égal au module du produit, il suffit de considérer les parties réelles et imaginaires du produit pour conclure.
Il est aussi possible d'établir directement l'identité sans référence aux nombres complexes :
Détails des démonstrations-
- Si un entier n est somme de deux carrés, alors le reste de la division de n par 4 n'est jamais égal à 3.
Cette propriété provient du fait que la division d'un carré par 4 ne peut donner pour reste qu'une des deux valeurs 0 ou 1. En effet, soit a un entier :
- S'il est pair, il existe un entier m tel que a est égal à 2.m. Le carré de a est égal à 4.m2 qui est un multiple de 4, le reste de la division par 4 est égal à 0.
- S'il est impair, il existe un entier m tel que a est égal à 2.m + 1. L'identité remarquable ci-dessous montre que son carré est la somme d'un multiple de 4 et de 1, le reste de la division par 4 est égal à 1.
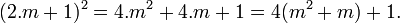
Si n est somme de deux carrés, notée n = a2 + b2, trois cas se présentent : a et b sont pairs, leurs carrés sont des multiples de 4 et leur somme est aussi un multiple de 4, l'un des deux est impair et l'autre pair alors la somme des carrés est la somme de deux multiples de 4 et de 1 et la division de la somme donne pour reste 1, enfin ils sont tous deux impairs et la somme des carrés est égal à la somme de deux multiples de 4 et de 2. Aucune configuration ne donne pour reste 3.
-
- Si deux entiers n et m sont sommes de deux carrés, alors leur produit est aussi somme de deux carrés.
Comme n et m sont sommes de deux carrés il existe quatre entiers a, b, c et d tel que les égalités suivantes soient vérifiées :
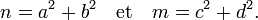
Cette proposition est la conséquence de l'identité de Brahmagupta, qui s'énonce de la façon suivante :

Pour s'en convaincre, il suffit de développer, puis factoriser le terme de droite :
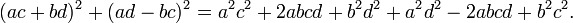
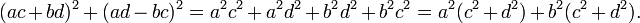
Une nouvelle factorisation montre l'égalité recherchée :
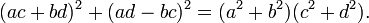
Conséquences de l'identité de Brahmagupta
L'identité de Brahmagupta permet d'aller plus loin dans l'analyse de l'équation. Elle permet de montrer que[42]:
-
- Si un nombre premier p est somme de deux carrés, alors les deux carrés sont uniques.
Une autre propriété est utile :
-
- Si un entier n, somme de deux carrés, est divisible par un nombre premier m, somme de deux carrés, alors le quotient est lui-même somme de deux carrés.
La démonstration est de même nature que la précédente, elle est fondée sur des calculs algébriques astucieux utilisant la même identité. Ce résultat peut être utilisé pour établir une preuve du théorème. Il permet d'avancer aussi l'analyse du cas général. Il permet par exemple de démontrer la proposition suivante, présente dans une des preuves du théorème :
-
- Si un nombre n, somme de deux carrés, est divisible par un nombre m, qui n'est pas somme de deux carrés, alors le quotient q contient un facteur premier qui n'est pas somme de deux carrés.
Détails des démonstrations-
- Si un nombre premier p est somme de deux carrés, alors les deux carrés sont uniques :
En effet, soit a2 + b2 et c2 + d2 deux sommes de deux carrés égal à p. On suppose ici que a, b, c et d sont quatre entiers positifs. Ils sont même strictement positifs, car si tel n'était pas le cas p serait un carré parfait, ce qui est impossible pour un nombre premier.
Montrons que p divise a.d - b.c et a.d + b.c. Pour cela, le calcul suivant est utile :
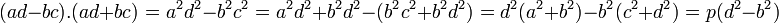
Le nombre premier p divise le produit de ad - bc par ad + bc. Le lemme d'Euclide montre que p divise l'un des deux facteurs. Si ad - bc est divisé par p, c'est-à-dire s'il existe un entier k1 tel que ad - bc = k1.p, on procède de la manière suivante. L'identité de Brahmagupta indique que :
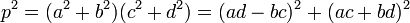
Ce qui montre que ac + bd est aussi un multiple de p et il existe un entier k2 tel que ac + bd = k2.p. L'égalité précédente s'écrit p2 = k12.p2 + k22.p2, et donc k12 + k22 est égal à un. Comme k1 et k2 sont deux entiers, l'un est nul l'autre est en valeur absolue égal à un. Il suffit de remarquer que ac + bd est strictement positif, car somme de produits de terme strictement positifs, pour conclure que k1 est nul, et ad - bc est aussi nul. Les deux vecteurs (a, b) et (c, d) sont proportionnels, ce qui montre l'existence d'un entier λ strictement positif tel que c = λ.a et d = λ.b. On en déduit que la somme c2 + d2 est égal à λ2.p et donc que λ est égal à un.
Si ad + bc est un multiple de p, l'égalité suivante montre que ac - bd est aussi un multiple de p :
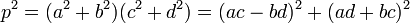
Le raisonnement précédent s'applique encore, il montre cette fois que a est égal à d et b à c. Les carrés sont identiques mais l'ordre est inversé.
-
- Si un entier n, somme de deux carrés, est divisible par un nombre premier m, somme de deux carrés, alors le quotient est lui-même somme de deux carrés :
Notons n = a2 + b2 et m = p2 + q2. Le raisonnement est analogue au précédent. Si n est divisible par le nombre premier m. Alors m divise le produit suivant :
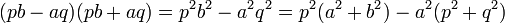
L'entier m est un nombre premier, le lemme d'Euclide indique qu'il divise l'un des deux facteurs, par exemple p.b - a.q. Comme lors de la démonstration précédente, l' identité de Brahmagupta montre que :
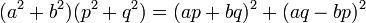
Ainsi, m divise (a.p + b.q)2, l'équation peut donc être divisée par le carré de m :
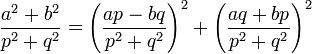
Ce qui démontre la proposition.
Si m2 divise p.b + a.q, un argument de même nature peut être utilisé avec :
 qui est une autre forme de l'identité de Brahmagupta.
qui est une autre forme de l'identité de Brahmagupta.-
- Si un nombre n, somme de deux carrés, est divisible par un nombre m, qui n'est pas somme de deux carrés, alors le quotient q contient un facteur qui n'est pas somme de deux carrés.
Notons q = q1.q2. ... .qk, la décomposition du quotient en facteurs premiers. Alors n = m.q1.q2. ... .qk. Si chaque facteur qi est somme de deux carrés, la proposition précédente montre qu'il est possible de diviser n successivement par chaque qi et d'obtenir chaque fois un entier somme de deux carrés. Ce raisonnement montre que m est alors somme de deux carrés. La contraposée montre que si m n'est pas somme de deux carrés, alors au moins un qi n'est pas somme de deux carrés.
Fermat et les résidus
Une autre étape de la démonstration consiste à étudier les restes de la division euclidienne par p de chacun des termes de l'équation x2 + y2 = p. Comme le reste du terme de droite est nul, celui du terme de gauche est aussi nul. Cette démarche revient finalement à trouver une solution à l'équation suivante :
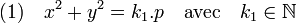
L'objectif est de trouver les solutions telles que ni x ni y ne soient des multiples de p. Comme p est premier, cela signifie que y et p sont premiers entre eux. L'identité de Bézout montre l'existence d'entiers α et β tels que :
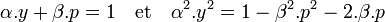
En multipliant par α2 l'équation (1) et en remplaçant α2.y2 par la valeur calculée précédemment, on obtient :
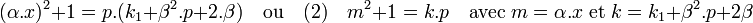
L'équation (2) admet toujours une solution si p est somme de deux carrés. Elle correspond à une simplification de l'équation générale, maintenant connue sous le nom du problème du résidu quadratique. Elle revient à déterminer dans quel cas un multiple d'un nombre premier s'écrit comme la somme d'un carré parfait et de un. Si p est un nombre premier différent de deux, la solution est donnée par la proposition suivante :
-
- Il existe un multiple de p s'écrivant comme somme d'un carré parfait et de un si et seulement si le reste de la division euclidienne de p par quatre donne pour reste un.
La condition est nécessaire, il a en effet déjà été démontré que le reste de la division euclidienne de m2 + 1 n'est jamais égal à trois. De nombreuses approches permettent d'établir la condition suffisante. L'une utilise le petit théorème de Fermat[43]. Une connaissance plus avancée en arithmétique modulaire permet une démonstration plus expéditive.
Démonstrations avec et sans arithmétique modulaire-
- Démonstration à base d'arithmétique modulaire :
La question revient à montrer que la classe de -1 est un carré dans le corps Z/pZ si p - 1 est égal à 4.n, avec n un entier strictement positif. Le groupe multiplicatif de (Z/pZ)* est un groupe cyclique comptant 4.n éléments. Soit g un générateur de ce groupe. L'élément -1 est l'unique élément du groupe différent de l'unité et dont le carré est égal à l'unité. Cet élément est égal à g2.n, il est effectivement différent de l'unité, sinon g ne serait pas un générateur et le théorème de Lagrange, équivalent du petit théorème de Fermat avec ce formalisme, montre que son carré est égal à un. La valeur gn est donc un élément du groupe multiplicatif dont le carré est égal à -1.
-
- Démonstration sans arithmétique modulaire :
Ici, n désigne encore l'entier tel que p = 4.n + 1. Le petit théorème de Fermat montre que si x est un entier, alors x4n - 1 = (x2n - 1).(x2n + 1) est un multiple de p. Comme p est premier, l'un des deux facteurs de l'égalité est un multiple de p. Il suffit de trouver un entier a tel que a2n - 1 n'est un multiple de p, alors a2n + 1 l'est nécessairement et an est la solution recherchée.
Considérons la suite de polynômes Pn[X] définie par récurrence de la manière suivante :
![P_0[X] = X^{2.n} - 1 \quad \text{et}\quad P_{i+1}[X] = P_i[X + 1] - P_i[X]](/pictures/frwiki/48/0f3249cb9b59893f1e75114d1c8027e0.png)
On remarque que si i est un entier compris entre 1 et 2.n, alors Pi[X] est un polynôme de degré 2.n - i et de monôme dominant ayant un coefficient égal au produit (2.n).(2.n - 1). ... .(2.n - i + 1 ). On en déduit que P2.n[X] est un polynôme constant égal à (2.n)! (ici le symbole ! désigne la fonction factorielle). Comme p est premier et supérieur à 2n, il n'est pas diviseur de (2.n)!. Or, P2.n[X], est combinaison linéaire à coefficients dans Z (l'ensemble des entiers), de valeurs que prend le polynôme P0[X] sur les entiers. Une de ces valeurs, notée a n'est donc pas un multiple de p. Comme P0[a] n'est pas un multiple de p, a2.n + 1 l'est, ce qui termine la démonstration.
Euler et la descente infinie
La démonstration d'Euler, présentée ici, suit exactement le plan indiqué par Fermat. Après l'utilisation du petit théorème de Fermat pour l'étude du résidu quadratique, il utilise la méthode de descente infinie. Cette méthode, souvent utilisée en arithmétique, se fonde sur les propriétés des entiers positifs. Elle propose des raisonnements par l'absurde fondée sur le fait qu'il n'existe pas dans N (l'ensemble des entiers positifs) de suite infinie strictement décroissante. La preuve consiste, à l'aide des hypothèses, à construire une suite infinie strictement décroissante d'entiers positifs. Comme une telle suite n'existe pas, il est démontré qu'une hypothèse est fausse.
Les démonstrations de cette nature s'appliquent plus naturellement pour l'obtention de propriété d'inexistence de solutions. Fermat l'utilise en particulier pour montrer une proposition équivalente à celle de son grand théorème pour n égal à quatre. La difficulté ici consiste à appliquer cette méthode pour démontrer un résultat positif : l'existence de solution[18]. Euler trouve une méthode astucieuse[43], il établit d'abord le lemme suivant en utilisant la descente infinie :
-
- Si un entier n est somme de deux carrés parfaits n = a2 + b2 et si a et b sont premiers entre eux, alors chaque facteur premier de n est somme de deux carrés.
Une fois ce résultat établi, la démonstration est brève. Le paragraphe précédent montre qu'il existe un entier k tel que k.p soit somme de deux carrés m2 + 12 . Les deux entiers m et un sont premiers entre eux car un est premier avec tous les entiers. Le facteur p est donc, d'après la proposition précédente, somme de deux carrés.
Détails de la démonstrationOn raisonne par l'absurde. On suppose qu'il existe un entier strictement positif n0 somme de deux carrés a2 + b2 et contenant un facteur premier qui ne soit pas somme de deux carrés. On suppose de plus que a et b sont premiers entre eux et quitte à intervertir les notations, on choisit a plus grand ou égal à b. L'entier n0 contient au moins deux facteurs premiers qui ne sont pas somme de deux carrés, car n0 est somme de deux carrés (cf la troisième proposition du paragraphe Conséquences de l'identité de Brahmagupta). Notons p le plus petit des deux et q l'entier tel que p.q soit égal à n0. L'entier q est plus grand que p car il contient un facteur au moins égal à lui.
L'objectif est construire un entier n1 strictement plus petit n0, strictement positif et possédant les mêmes propriétés. Remarquons que :

Soit α1 (resp. α2) les entiers positifs et r1 (resp. r2) les entiers en valeur absolue inférieur à la moitié de p tel que :
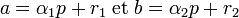
En remplaçant a et b par leurs valeurs, on obtient :
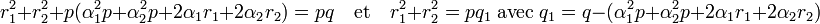
L'objectif est de montrer que q est strictement plus grand que q1. On remarque que :
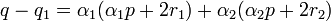
Les définitions de r1 et r2 montre que la différence est toujours positive. La majoration (3) montre que α1 est strictement positif, le terme α1(α1 + 2r1) n'est nul que si p est égal à -2r1 et α1 est égal à un. Dans ce cas p est égal à 2.a. Cette configuration est impossible car alors a et b ne peuvent être premiers entre eux. La différence est donc toujours strictement positive.
Une propriété n'est pas encore assurée. Rien ne garantit que les valeurs absolues de r1 et r2 sont premières entre elles. Supposons qu'elles admettent un diviseur commun et notons d leur plus grand commun diviseur. d ne peut diviser p car il diviserait alors a et b qui sont premiers entre eux. En conséquence d divise q1. Soit a' (resp. b' ) le quotient de la valeur absolue de r1 (resp. r2) par d et q'1 le quotient de q1 par d 2. Notons n1 le produit de p par q'1. Alors a' et b' sont deux entiers positifs premiers entre eux tels que :
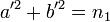
Et l'entier n1 contient un facteur premier p qui n'est pas somme de deux carrés. En réitérant le raisonnement, il existe une suite (ni) strictement décroissante et infinie d'entiers positifs. La logique de la méthode de la descente infinie permet de conclure que chaque facteur premier de n0 est somme de deux carrés.
Lagrange et les formes quadratiques
Si la démonstration d'Euler possède l'avantage de clore une conjecture de plus d'un siècle, elle est difficilement généralisable et ne permet guère de progresser sur l'équation diophantienne x2 + n.y2 = p.
Lagrange utilise une démarche moins entachée de cette faiblesse. Il considère l'expression x2 + y2 comme la forme quadratique associée au produit scalaire canonique. Cette approche élargit considérablement la liste des outils disponibles, ceux de l'algèbre linéaire en font maintenant parti. La situation n'est néanmoins pas celle la plus fréquemment rencontrée. Le produit scalaire n'est pas défini sur un espace vectoriel mais sur le module Z2. Un module est une structure comparable à celle d'espace vectoriel, à la différence près que l'ensemble des scalaires n'est plus un corps. Pour les modules de cette nature, certains résultats restent vrais, comme par exemple l'existence d'une base ce qui offre une expression algébrique simple.
Si M est la matrice de passage de la base canonique dans une autre base sur Z2, son déterminant est nécessairement égal à 1 ou -1. En effet, une matrice de passage est inversible :
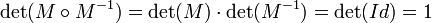
Ici Id désigne la matrice identité. Comme les coefficients de la matrice sont entiers, le déterminant l'est aussi. L'égalité précédente montre que le déterminant de M est inversible et comme les seuls entiers inversibles sont 1 et -1, ce sont les seules valeurs possibles. La matrice du produit scalaire canonique est l'identité. Dans une base quelconque, la matrice est donc de la forme tM.M (ici tM désigne la matrice transposée de M). Une telle matrice est symétrique et de déterminant égal à un car la transposition ne modifie pas le déterminant. Comme le produit scalaire est défini positif, les coefficients diagonaux sont positifs. Réciproquement, Lagrange établit le résultat suivant :
-
- Toute forme bilinéaire sur Z2 dont la matrice est symétrique, de coefficients diagonaux positifs et de déterminant égal à un, admet une base orthonormale.
Ainsi l'image par la forme quadratique associée d'un vecteur de coordonnées (x, y) dans la base orthonormale est égale à x2 + y2. Lagrange choisit la forme bilinéaire φ de matrice M suivante :
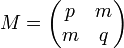
Ici, p désigne le nombre premier congru à un modulo quatre et m et q des entiers. La matrice M possède un déterminant égal à un si et seulement si m2 + 1 = p.q. Cette équation est bien connue et déjà traitée. Elle correspond à l'étude du résidu quadratique -1 sur le modulo p. Elle admet une solution si et seulement si p est congru à un modulo quatre.
Soit u le vecteur de coordonnées (1, 0), un calcul élémentaire montre que φ(u, u) = p. Si a et b sont les coordonnées de u dans la base orthonormale, alors l'expression de φ(u, u) devient a2 + b2, ce qui démontre le théorème[44].
Démonstration de l'équivalence des différentes formes quadratiquesLa démonstration proposée ici est plus riche que celle nécessaire pour démontrer le théorème des deux carrés de Fermat. Si l'objectif est uniquement de prouver le théorème, il suffit de résoudre l'équation (1), ce qui est fait en partie 3) de la démonstration présentée ici.
La démonstration proposée ici montre l'existence d'une base orthonormale pour la forme bilinéaire φ dont la matrice dans la base canonique est égale à M. Dans un premier temps, trouvons un vecteur u ayant pour image par φ l'entier un. Notons (x0, y0) ses coordonnées, entières par définition. Z2 est inclus dans R2 (ici R désigne l'ensemble des nombres réels), la base canonique est aussi une base de R2 et la matrice M permet de prolonger φ sur R2. Soit ψ la forme quadratique associée à φ.
1. Détermination de la coordonnée yR dans R tel que le vecteur de R2 (x0, yR) soit minimal par ψ.
L'application qui à y associe l'image par ψ du vecteur de coordonnées (x0, y) est parabolique et admet un minimum dans R noté yR. On a :
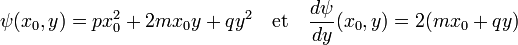
Si m est égal à zéro, le calcul du déterminant montre que p et q sont égaux à un et φ possède bien une représentation matricielle égale à l'identité. Si m est différent de zéro, alors q l'est aussi et :
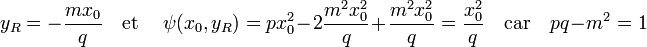
2. Détermination des propriétés de y0.
Le point y0 est l'entier le plus proche de yR. Soit h0 la distance entre ces deux points, c'est à dire le réel inférieur à 1/2 en valeur absolue satisfaisant l'égalité : y0 = yR + h0. Ces points vérifient les égalités :
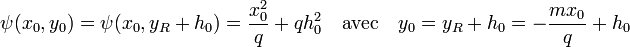
Trouver le point u revient à trouver un vecteur de coordonnées entières (x0, y0) d'image par ψ strictement inférieur à deux, c'est à dire si r 0 est égal à q.h0 :
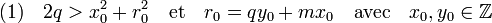
3. Existence de u.
Soit ri le résultat de la division euclidienne de m.i par q, θ l'entier positif tel que θ2 est plus petit ou égal à q et θ2 + 1 est strictement plus grand que q. Considérons l'ensemble des intervalles [i.θ + 1, (i + 1).θ] où i décrit les entiers de zéro à θ et la suite finie (rj) où j décrit les entiers de un à θ.
S'il existe un élément de la suite finie rk se situant dans l'intervalle [0, θ] alors les valeurs k pour x0 et rk pour r0 satisfont les propriétés (1). En effet, rk au carré est plus strictement plus petit que q et k2 + rk2 est strictement plus petit que 2q. Si rk se situe dans le dernier intervalle, alors les valeurs k pour x0 et q - rk pour r0 satisfont encore les propriétés (1). Dans les deux cas, il est possible de construire le vecteur u.
On remarque que la suite (ri) contient θ éléments et qu'il existe θ + 1 intervalles. En conséquence, soit au moins l'un des intervalles extrêmes est couvert par un élément de la suite, soit un intervalle contient deux termes rk et rl (choisissons k plus grand que l). La distance entre les deux termes de la suite est strictement inférieure à θ, en conséquence r k-l est à une distance strictement inférieure à θ de l'un des points 0 ou q et le système (1) admet encore une solution u obtenue avec x0 égal à k-l et pour r0 le minimum de r k-l et q - r k-l.
4. Existence de v tel que (u, v) soit orthonormale pour le produit scalaire φ :
Une fois le vecteur u trouvé, la recherche du deuxième vecteur est plus aisée. Soit Θ la rotation d'un quart de tour dans le sens direct et a l'application linéaire de matrice M dans la base canonique. Soit v l'image de u par aoΘ. Les vecteurs u et v sont bien orthogonaux pour la forme bilinéaire φ. En effet, il suffit de remarquer que a est orthogonal et, si (.,.) désigne le produit scalaire canonique alors :
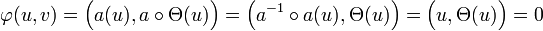
On remarque ensuite que ψ(v) est égal à un :

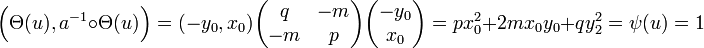
Gauss et ses entiers
Article détaillé : Entier de Gauss.L'adjonction d'une géométrie euclidienne à la question des deux carrés est d'un incontestable apport. Elle permet d'introduire les outils de l'algèbre linéaire dans l'arithmétique. Elle ouvre cependant plus de questions qu'elle n'en résout. Bien peu d'outils restent disponibles pour attaquer le cas général. Gauss propose un nouvel enrichissement structurel de l'ensemble des couples de coordonnées entières. Le plan, qui dispose déjà d'une addition, d'un produit externe par un élément de Z et d'une forme quadratique, est en plus équipé d'une multiplication interne. Le point (a, b) de coordonnées entières est identifié au complexe a + i.b. L'ensemble des points dispose alors d'une structure d'anneau dont les éléments sont appelés entiers de Gauss.
La forme quadratique est maintenant interprétée comme une norme. À un point z est associé la norme N(z) définie par le produit de z et de son conjugué. La norme dispose d'un double avantage aux yeux du théorème sujet de l'article, la question posée s'exprime sous une forme simple N(z) = p et la norme est une valuation de l'anneau. Une valuation est ici une application qui à un entier de Gauss associe un entier naturel (le terme entier naturel désigne ici un élément de Z) positif et qui respecte la multiplication, c'est-à-dire si Z[i] désigne l'ensemble des entiers de Gauss :
![\forall z_1,z_2 \in \mathbb Z[i]\quad N(z_1.z_2)=N(z_1).N(z_2)\;](/pictures/frwiki/52/4202badda5ae4826a098561bab540c73.png)
 Richard Dedekind est l'auteur de la démonstration proposée ici.
Richard Dedekind est l'auteur de la démonstration proposée ici.
Elle possède l'avantage de conférer à l'anneau une structure euclidienne, c'est-à-dire que l'anneau dispose d'une division euclidienne. Ainsi, si n et m sont deux entiers de Gauss :
![\exists d,r \in \mathbb Z[i]\quad n = d.m + r\quad \text{avec}\quad N(r)<N(d)](/pictures/frwiki/48/03d38cbf13a03eb9ee554035caf29659.png)
Tout anneau euclidien est aussi factoriel, ce qui signifie que le théorème fondamental de l'arithmétique s'applique encore. Il existe ainsi des nombres premiers de Gauss et une décomposition unique en facteur premiers, aux entiers inversibles près.
Ce nouveau cadre structurel autorise la démonstration du théorème en quelques lignes. Si p est un nombre premier congru à 1 modulo 4, l'objectif est de montrer l'existence d'un entier z tel que N(z) = p. Le résultat sur le résidu quadratique -1 montre qu'il existe deux entiers naturels positifs m et k tel que N(m + i) = k.p. On en déduit l'égalité suivante :
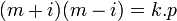
Cette égalité permet de déduire que p n'est pas premier comme entier de Gauss. S'il l'était, il diviserait m + i ou m - i, ainsi que son conjugué. Ainsi il diviserait l'un et l'autre ainsi que leur différence -2.i. Or l'entier de Gauss p ne divise pas -2.i car sa norme est trop grande. Il existe donc deux entiers de Gauss z1 et z2, qui ne sont pas des unités et tel que z1.z2 est égal à p. Comme les diviseurs ne sont pas des unités, leur normes sont différentes de 1 et N(z1).N(z2) = p2. Comme p est premier, les seuls diviseurs de p2 sont 1, p et lui-même. On en déduit que N(z1) est égal à p, ce qui termine la démonstration.[45]
Résultats connexes
Autres problèmes posés par Fermat
Quatorze ans plus tard, dans une lettre à Blaise Pascal, Fermat conjecture deux résultats analogues si p est un nombre premier impair :
Ces deux résultats sont pour la première fois démontrés par Lagrange.
DémonstrationLa démonstration ici est analogue à celle de Dedekind, cependant, l'anneau des entiers est celui d'Eisenstein. Il est composé des nombres complexes de la forme a + b.j où j désigne la racine cubique de l'unité
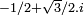 . C'est aussi un anneau euclidien et donc factoriel.
. C'est aussi un anneau euclidien et donc factoriel.1. Si un nombre premier différent de trois est de la forme x2 + 3.y2 alors il est congru à un modulo trois.
-
- En effet, le deuxième terme est congru à zéro, modulo trois, un carré est congru à zéro ou à un. En conséquence, si p est différent de trois, comme il est premier, il n'est pas congru à zéro modulo trois il est donc congru à un.
2. Si p est différent de trois et congru à un modulo trois, alors il existe un entier α tel que α2 + 3 soit un multiple de p.
-
- Soit le polynôme X3 - 1 dans Z/pZ. Ces racines sont les éléments d'ordre trois dans le groupe (Z/pZ)* qui est un groupe cyclique d'ordre p - 1 (cf Groupe cyclique et anneau). Il en existe trois si et seulement si l'ordre du groupe est un multiple de trois (cf la troisième proposition du Théorème fondamental des groupes cycliques). Le polynôme se factorise de la manière suivante :
- Et le polynôme X2 + X + 1 admet une racine J dans Z/pZ si, et seulement si, p est congru à un modulo trois. Il suffit alors de remarquer que le carré de 1 + 2.J est égal à -3. Ce qui montre que tout élément α de la classe de 1 + 2.J remplit la condition.
- Soit le polynôme X3 - 1 dans Z/pZ. Ces racines sont les éléments d'ordre trois dans le groupe (Z/pZ)* qui est un groupe cyclique d'ordre p - 1 (cf Groupe cyclique et anneau). Il en existe trois si et seulement si l'ordre du groupe est un multiple de trois (cf la troisième proposition du Théorème fondamental des groupes cycliques). Le polynôme se factorise de la manière suivante :
3. Il existe un entier d'Eisenstein de norme égale à p, si p est congru à un modulo trois.
-
- p divise (α + √3.i).(α - √3.i). De plus il ne divise aucun des membres car s'il en divise un, il divise l'autre (c'est son conjugué) et il divise leur différence égale à 2√3.i. Or p ne divise pas 2√3.i, il n'est donc pas irréductible. Et il existe deux entiers d'Eisenstein n et m non unitaires tel que p = n.m et comme la norme de p est égale à p2 et qu'une norme est toujours un entier, la norme de n est égale à p. La proposition est démontrée.
4. Il existe deux entiers x et y tel que x2 + 3.y2 soit égal à p, si p est congru à un modulo trois.
-
- Le point 3. montre l'existence de deux entiers a et b tel que n = a + b.j ait pour norme p. Cependant un entier de la forme a + b.j est de la forme x + y.√3.i si, et seulement si, b est pair. On remarque que la norme de n est égal à a2 - a.b + b2. a et b ne peuvent être pair en même temps car p serait alors un multiple de quatre, or p est premier. Si a est pair, alors b + a.j possède une norme égale à p et un coefficient pair pour j. Si a et b sont impairs alors a + (a - b).j possède une norme égale à p et un coefficient pair pour j.
Une démonstration est proposée dans l'article Entier quadratique.
Généralisation à tous les entiers
Une fois connu les nombres premiers somme de deux carrés, il devient possible de généraliser la question à tous les entiers:
-
- Un entier n est somme de deux carrés d'entiers si, et seulement si, dans sa décomposition en facteurs premiers, les nombres premiers congrus à 3 modulo 4 figurent à une puissance paire.
Ce résultat peut s'énoncer de la manière suivante:
Un entier est somme de deux carrés d'entiers si et seulement si les valuations p-adiques des facteurs premiers p de n congrus à 3 modulo 4 sont paires.
DémonstrationUn lemme est utile pour la démonstration de ce théorème:
-
- Soit p un nombre premier congru à 3 modulo 4. Si une somme de deux carrés d'entiers a2 + b2 est un multiple de p alors a et b sont des multiples de p.
Si a2 + b2 est congru à 0 modulo p et si b n'est pas un multiple de p alors a/b est solution de l'équation X2 + 1 = 0 dans Z/p Z. Il n'existe pas de telle solution d'après la démonstration du théorème des deux carrés de Fermat. Donc b est un multiple de p et par voie de conséquence a aussi.
-
- Démonstration du théorème :
Si p est de la forme décrite dans le théorème, alors la puissance de deux s'écrit soit (2m + 0) si m est paire soit (2m-1 + 2m-1) si m est impaire. Les nombres premiers congrus à 1 modulo 4 s'écrivent tous sous forme de somme de deux carrés et les puissances paires de nombres premiers congrus à 3 modulo 4 s'écrivent toutes sous une forme du type (p2 + 0)m. Alors n est produit de sommes de deux carrés et le premier lemme permet de conclure.
Réciproquement supposons que n est somme de deux carrés d'entiers n = a2 + b2. Soit p un nombre premier congru à 3 modulo 4 élément de la décomposition en facteurs premiers de n. Le deuxième lemme montre que a et b sont des multiples de p. En conséquence a2 + b2 est un multiple d'un carré de p. Ce qui permet de conclure que toutes les puissances congrues à 3 modulo 4 sont paires.
Voir aussi
Notes
- ↑ Euclide, Les Éléments, traduction, commentaires et notes de Bernard Vitrac [détail des éditions], vol. 3, Livre X, pp. 171-176.
- ↑ Diophante d'Alexandrie, Les six livres arithmétiques, trad. P. Ver Ecke, Paris: Albert Blanchard, 2000 (ISBN 2853671577). La numérotation des problèmes varie d’une édition à l’autre, on utilise ici celle de cette édition. Ces six livres, les seuls connus jusqu’à une époque récente, font en fait partie d’un ensemble originellement plus vaste de 13 livres. Quatre autres livres ont été retrouvés dans une version arabe vers 1970, cf. Diophante, Les Arithmétiques, Paris : Les Belles Lettres, 1984, 2 volumes parus.
- ↑ Cette traduction est celle de P. Ver Ecke, citée plus haut.
- ↑ (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], ch. I, § 6.
- ↑ Diophante ajoute une autre condition, mais malheureusement, le texte qui a survécu est corrompu et peu clair, de nombreuses interprétations en ont été proposées, qui attribuent à Diophante une compréhension plus ou moins complète des conditions pour qu’un nombre soit somme de carrés, voir par exemple dans (en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions], vol. 2, p. 225 ou Ver Ecke, commentaire des Arithmétiques de Diophante, op. cit., p. 197.
- ↑ R. Rashed, « Analyse combinatoire, analyse numérique, analyse diophantienne et théorie des nombres », in Histoire des sciences arabes, vol. 2, Paris : Seuil, 1997, p. 80-85.
- ↑ (en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions], vol. 2, p. 227 ; Edouard Lucas Recherches sur l'analyse indéterminée et l'arithmétique de Diophante Bulletin de la Société d'émulation de l'Allier 1873 Lire sur Gallica
- ↑ Diophante Arithmetica édition grecque et traduction en latin commentée de Claude-Gaspard Bachet de Méziriac, Paris 1621
- ↑ Dans la deuxième édition de son livre, Problèmes plaisans et délectables, qui se font par les nombres, partie recueillis de divers auteurs, et inventez de nouveau, avec leur démonstration, par Claude Gaspar Bachet, Sr. de Méziriac. Très utiles pour toutes sortes de personnes curieuses qui se servent d'arithmétique (1624), Bachet donne aussi la première preuve actuellement connue de l'identité de Bezout
- ↑ Cette identité est souvent appelée identité de Brahmagupta car on l'a trouvée aussi sous une forme légèrement différente chez cet auteur indien du 7e siècle
- ↑ Fermat préfère les écrire sous la forme 4’’k’’-1, ce qui revient bien sûr au même.
- ↑ Fermat ajoute : « en quoi j’ai ... rétabli en même temps la corruption du texte de Diophante », s’inscrivant ainsi dans une longue lignée de mathématiciens érudits qui ont cherché à la fois à reconstituer le texte de Diophante et à trouver la solution complète du problème sous-jacent !
- ↑ Fermat, Œuvres complèteséditées par C. Henry & P. Tannery, 4 vols., 1891–1912, vol. II, p. 203-204
- ↑ Lettre du 25 décembre 1640 de Fermat à Mersenne, Œuvres complèteséditées par C. Henry & P. Tannery, 4 vols., 1891–1912, vol. II, p. 213.
- ↑ Le théorème complet et des applications figure dans une observation au livre III, un cas particulier au livre V, près du problème 12 de Diophante mentionné plusieurs fois.
- ↑ Pierre de Fermat Oeuvres complètes, éditées par C. Henry & P. Tannery, 4 vols Tome II p 334 1891–1912.
- ↑ Les détails de l'utilisation de cette méthode par Fermat sont explicités dans, C. Goldstein Un théorème de Fermat et ses lecteurs Saint-Denis, Presses Universitaires de Vincennes 1995 (ISBN 2910381102).
- ↑ a et b Pierre de Fermat, Oeuvres complètes, éditées par C. Henry & P. Tannery, 4 vols., 1891–1912, vol. II, p 441 ; Lire
- ↑ Par exemple, Edouard Lucas, Recherches sur l'analyse indéterminée et l'arithmétique de Diophante, 1873 ou (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions] ; voir aussi la preuve donnée plus bas dans cet article.
- ↑ Pierre de Fermat Oeuvres complètes, éditéés par C. Henry & P. Tannery, 4 vols., 1891–1912 Tome II p313, 403 et 405
- ↑ A. Weil Sur les origines de la géométrie algèbrique Compositio Mathematica 44 n° 1-3, p 399 lire
- ↑ Lire.
- ↑ Pour le détail délicat des dates et des publications des différents résultats, voir (en) Leonard Eugene Dickson, History of the Theory of Numbers [détail des éditions], vol. 2, chap. VI, et (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], chapitre 3, §5b e, IX et XI.
- ↑ Leonhard Euler Observationes circa divisionem quadratorum per numeros primos Opuscula analytica 1, 1783, p. 64-84 lire
- ↑ Voir (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], chapitre 3, §X.
- ↑ On ne sait toujours pas si cette liste est complète, mais on sait qu'elle contient au plus 66 nombres.
- ↑ Nouveaux mémoires de l'Académie royale des sciences et belles lettres de Berlin, première partie, 1775, supplément 1777, rep. dans Joseph-Louis Lagrange, Œuvres, vol. III, pp. 695-758 et 759-795. Le théorème est démontré sous le nom de Lemme VII pp. 782-783. Quelques années auparavant, en 1772, Lagrange a démontré un autre résultat connexe, le théorème des quatre carrés, le fait que tout nombre entier peut s'écrire comme une somme de 4 carrés, voir (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], chap. IV, § II (D).
- ↑ Il faut remarquer que Lagrange ne considère que des formes à coefficients entiers, l'étude des formes à coefficients réels ne commencera qu'un demi-siècle plus tard.
- ↑ Cette condition indique que la transformation est inversible.
- ↑ (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], chap. IV, § 4.
- ↑ (en) André Weil, Number Theory: An Approach through History, from Hammurapi to Legendre [détail des éditions], chap. IV, § 4.
- ↑ Il trouve une démonstration à condition d'admettre le théorème de la progression arithmétique, question qui s'avère encore plus difficile que celle de la réciprocité quadratique et ne sera démontrée qu'en 1837 : Adrien-Marie Legendre, Essai sur la théorie des nombres, Duprat, Paris, 1798
- ↑ Legendre considère que dès 1830, parler de théorie des nombres n'est pas abusif : On a cru devoir lui donner définitivement le titre de Théorie des nombres au lieu de celui d'essai sur cette Théorie qu'il avait porté jusqu'à présent : Adrien-Marie Legendre Théorie des nombres Firmin-Didot Paris 1830 lire sur Gallica
- ↑ Carl Friedrich Gauss Recherches arithmétiques trad. française des Disquisitiones arithmeticae par A.-C.-M. Poullet-Delisle 1801 lire
- ↑ Carl Friedrich Gauss Recherches arithmétiques trad. française des Disquisitiones arithmeticae par A.-C.-M. Poullet-Delisle 1801 article 182
- ↑ Carl Friedrich Gauss Recherches arithmétiques trad. française des Disquisitiones arithmeticae par A.-C.-M. Poullet-Delisle 1801 p 96 lire
- ↑ Carl Friedrich Gauss Recherches arithmétiques trad. française des Disquisitiones arithmeticae par A.-C.-M. Poullet-Delisle 1801 p 338 lire
- ↑ Charles Gustave Jacob Jacobi Fundamenta nova theoriae functionum ellipticarum Königsberg, 1829
- ↑ Richard Dedekind Vorlesungen über Zahlentheorie. Hrsg. und mit Zusätzen versehen von R. Dedekind. 4. umgearb. u. verm. Aufl. Braunschweig 1894. La preuve est proposée dans le supplément XI rédigée par Dedekind, le texte principal est une publication par Dedekind d'un travail de Dirichlet intitulé Leçons en théorie des nombres
- ↑ Cette analyse est un résumé de : F. Lemmermeyer The development of the principal genus théorem lire
- ↑ David Hilbert Über die Theorie der relativquadratischen Zahlkörper Jahresber. DMV 6 1899
- ↑ On peut trouver cette démonstration, par exemple sur le site Les théorèmes orphelins par J.-M. Breton
- ↑ a et b La démonstration proposée est celle d'Euler. Elle est disponible en latin sur le web Lire
- ↑ Cette démonstration est celle de Lagrange avec les notations (mondernisées) de Gauss que l'on trouve dans la référence : Carl Friedrich Gauss Disquisitiones Aritmeticae Traduction française par Poullet-Delisle en 1807 lire sur Gallica Article 185
- ↑ Cette preuve est l'œuvre de Richard Dedekind, l'orginal est publié dans : Richard Dedekind Vorlesungen über Zahlentheorie. Hrsg. und mit Zusätzen versehen von R. Dedekind. 4. umgearb. u. verm. Aufl. Braunschweig 1894. La preuve est proposée dans le supplément XI rédigée par Dedekind, le texte principal est une publication par Dedekind d'un travail de Dirichlet intitulé Leçons en théorie des nombres
Liens externes
- (fr) Somme de carrés
Une présentation didactique et expérimentale par G. Yoda
- (fr) Sur les sommes de carrés
Plusieurs démonstrations du théorème utilisant des outils plus ou moins sophistiqués par Gilles Auriol
- (fr) Les entiers de Gauss et le théorème des deux carrés
Une présentation plus technique du théorème, par B. Edixhoven, L. Moret-Bailly un cours de maîtrise de l'Université de Rennes 1 qui traite du théorème en page 9
- (fr) Somme de deux carrés
Un bref énoncé du théorème par Bibmath avec des liens vers les entiers de Gauss et le théorème de la somme des quatre carrés
- (en) Conséquences arithmétiques du théorème de Jacobi sur le théorème des deux carrés
Une démonstration du résultat de Jacobi par M. D. Hirschhorn
Références
Didactique
- (fr) M. Guinot Arithmétique pour amateurs. Vol. 1. Pythagore, Euclide et toute la clique Aléas Lyon, 1992 (ISBN 2908016214)
Cette série de cinq volumes s'adresse aux amateurs éclairés (c'est-à-dire ayant fait une ou deux années d'études mathématiques après le baccalauréat). On y trouve les bases de l'arithmétique ainsi que l'étude des triplets pythagoricien.
- (fr) M. Guinot Arithmétique pour amateurs. Vol. 2. Les resveries de Fermat Aléas Lyon, 1993 (ISBN 2908016273)
La troisième partie concerne les sommes de deux carrés.
- (fr) M. Guinot Arithmétique pour amateurs. Vol. 3. Ce diable d'homme d'Euler Aléas Lyon, 1994 (ISBN 2908016397)
Ce livre traite du théorème des deux carrés avec les outils de Lagrange et de Jacobi ainsi que de l'équation diophantienne en général.
- (fr) M. Guinot Arithmétique pour amateurs. Vol. 5. GAUSS "princeps mathematicum" Aléas Lyon, 1997 (ISBN 2843010446)
Ce livre traite des entiers de Gauss et de la classification des formes quadratiques.
Historique
- (en) T. L. Heath Diophantus of Alexandria: A Study in the History of Greek Algebra Dover Publications, Inc., New York, 1964
- (en) L. E. Dickson History of the Theory of Numbers Amer Mathematical Society 1999 (ISBN 0821819380)
Ce monumental traité de plus de 1500 pages traite largement Diophante au chapitre II. On y trouve par exemple une analyse précise du contenu mathématiques que le formalisme antique rend complexe.
- (fr) C. Goldstein Un théorème de Fermat et ses lecteurs Presses universitaires de Vincennes 1995 (ISBN 2910381102)
Ce texte traite à la fois du contexte historique et des différents lectures et regards des mathématiciens sur l'œuvre de Fermat. En revanche, le théorème traité n'est pas celui de l'article, même si les outils utilisés sont analogues.
- (en) R. E. Bradley Leonhard Euler: Life, Work and Legacy Elsevier Science 2007 (ISBN 0444527281)
Ce livre est un assemblage de 24 articles sur Euler pour l'anniversaire de son 300ième anniversaire. Le contenu arithmétique de son œuvre ainsi que son influence historique sont traités.
Mathématiques
- (fr) I.R.E.M. Lille Les nombres - Problèmes anciens et actuels Ellispe 2000 (ISBN 2729801227)
- (fr) Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
Cette référence est l'une des plus citées comme introduction à la théorie algébrique des nombres. On y trouve les théorèmes des deux, trois et quatre carrés.
- (fr) Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
Cette référence comme la précédente, est l'une des plus célèbres introductions à la théorie algébrique des nombres.
- (fr) R. Descombes Éléments de théorie des nombres PUF 1986 (ISBN 213039214-8)
On y trouve une démonstration fondée sur l'approche de Lagrange en page 12 et 13.
- (en) D. A. Cox Primes of the Form x2+ny2 Wiley-Interscience 1989 (ISBN 0471506540)
Le livre est technique et couvre dans son intégralité la question du titre, une bonne référence pour aller plus loin.
- (en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions]
Ce livre est un ouvrage didactique, déjà ancien mais de nombreuses fois réactualisé, et faisant toujours référence comme introduction à la théorie des nombres. Il contient les démonstrations de tous les résultats de l'article, par exemple celui de Jacobi au paragraphe 9 du chapitre 16.
- Portail des mathématiques
Catégories : Théorème d'algèbre | Équation diophantienne | Arithmétique modulaire | Entier quadratique -
Wikimedia Foundation. 2010.