Methode de descente infinie

Methode de descente infinie

Méthode de descente infinie

La méthode de descente infinie est un argument mathématique voisin de la démonstration par récurrence, mais aussi de la démonstration par l'absurde, qui utilise le fait qu'une suite d'entiers naturels strictement décroissante est nécessairement finie. Cette méthode repose sur l'un des axiomes des entiers naturels : tout ensemble non vide d'entiers naturels possède un plus petit élément.

Sommaire

Principe

Soit P(n) une propriété faisant intervenir un entier n. On cherche à démontrer que P(n) est fausse pour tout n. Pour cela on suppose que pour un entier a quelconque, P(a) est vraie. Par un argument mathématique à préciser dans chaque cas, on montre que si P(n) est vraie, alors P(m) est également vraie pour un entier m strictement inférieur à n. On peut alors conclure que P(n) n'est jamais vraie car la suite des entiers naturels vérifiant la propriété P(n) ne peut jamais être strictement décroissante et infinie.

Cette méthode sert essentiellement à démontrer qu'il n'existe pas d'élément entier répondant à une certaine propriété en construisant une nouvelle solution entière strictement plus petite que la précédente (en un sens à préciser dans chaque cas). Si une supposition induit la possibilité de l'existence d'une suite infinie et strictement décroissante d'entiers naturels alors cette supposition est fausse : en effet on construirait ainsi un entier qui serait plus petit que le plus petit des entiers répondant au problème posé.

Limites

On remarque que la descente infinie repose sur l'existence d'une taille (hauteur, norme, longueur...) entière et positive pour chaque solution. Elle ne s'applique donc pas à des tailles prises dans l'ensemble des entiers relatifs où la suite définie par u0 = a et un + 1 = un − 1 est strictement décroissante et infinie. Elle ne s'applique pas non plus à des tailles dans l'ensemble des rationnels (même si l'on se restreint aux rationnels positifs) où la suite 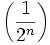\left (\frac {1}{2^n}\right) est strictement décroissante et infinie.

Exemples

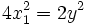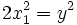  • Pour montrer qu'il n'existe pas d'entiers naturels non nuls x et y tels que x2 = 2y2 (1), on suppose qu'il existe de tels entiers, alors x serait pair et s'écrirait 2x1. L'égalité (1) s'écrirait 4x_1^2 = 2y^2, puis 2x_1^2 = y^2.
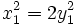On aurait alors y pair. Il s'écrirait 2y1. Les entiers x1 et y1 vérifieraient de nouveau x_1^2 = 2y_1^2.
Ainsi de suite, on pourrait créer une suite infinie et strictement décroissante d'entiers naturels vérifiant (1).
Absurde donc il n'existe pas d'entiers naturels non nuls x et y tels que x2 = 2y2.

Histoire

Cette méthode apparaît dans les Éléments d'Euclide, mais c'est surtout Pierre de Fermat qui la formule explicitement et en fait un instrument important dans son programme pour la théorie des nombres entiers[1] ; elle apparaît en particulier dans sa preuve du théorème que la surface d'un triangle rectangle dont les côtés sont entiers ne peut être le carré d'un entier, preuve qui constitue son Observation 45 sur les Arithmétiques de Diophante et qui a été publiée pour la première fois en 1670, dans l'édition posthume de ces observations qu'en fit Samuel de Fermat. Ce théorème entraîne la démonstration du dernier théorème de Fermat pour n=4. Frenicle de Bessy se sert aussi de la méthode de descente infinie, d'après Fermat, dans son Traité des triangles rectangles en nombres, édité en 1676. Elle a été aussi utilisée par Euler pour établir la démonstration du théorème des deux carrés de Fermat, et dans de nombreuses recherches de théorie des nombres. Une variante a été mise en particulier en œuvre pour démontrer le théorème de Mordell-Weil selon lequel la structure des points à coordonnées rationnelles (ou plus généralement à coordonnées dans un corps de nombres) sur une courbe elliptique est un groupe abélien de type fini.

Note

  1. ↑ Lettre à Carcavi, 1659

Références

W. H. Bussey, Fermat's Method of Infinite Descent, The American Mathematical Monthly 25, 333-337

P. Bussotti, Der "unendliche Abstieg" von Fermat bis Gauß, Rauner, 2006.

R. Cassinet, Histoire de la descente infinie de Campanus à Hilbert, Cahier du séminaire d'histoire des mathématiques de Toulouse 2: B, 1-25.


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « M%C3%A9thode de descente infinie ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode de descente infinie de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Méthode De Descente Infinie — La méthode de descente infinie est un argument mathématique voisin de la démonstration par récurrence, mais aussi de la démonstration par l absurde, qui utilise le fait qu une suite d entiers naturels strictement décroissante est nécessairement… …   Wikipédia en Français

  • Méthode de descente infinie — La méthode de descente infinie est un argument mathématique voisin de la démonstration par récurrence, mais aussi de la démonstration par l absurde, qui utilise le fait qu une suite d entiers naturels strictement décroissante est nécessairement… …   Wikipédia en Français

  • Descente infinie — Méthode de descente infinie La méthode de descente infinie est un argument mathématique voisin de la démonstration par récurrence, mais aussi de la démonstration par l absurde, qui utilise le fait qu une suite d entiers naturels strictement… …   Wikipédia en Français

  • Théorème de descente infinie — Méthode de descente infinie La méthode de descente infinie est un argument mathématique voisin de la démonstration par récurrence, mais aussi de la démonstration par l absurde, qui utilise le fait qu une suite d entiers naturels strictement… …   Wikipédia en Français

  • Descente De Gradient — Traduction à relire Gradient descent → …   Wikipédia en Français

  • Descente de gradient — Traduction à relire Gradient descent → …   Wikipédia en Français

  • Algorithme de descente — Descente de gradient Traduction à relire Gradient descent → …   Wikipédia en Français

  • Demonstrations du dernier theoreme de Fermat — Démonstrations du dernier théorème de Fermat Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Démonstration du dernier théorème de Fermat — Démonstrations du dernier théorème de Fermat Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

  • Démonstration du théorème de Fermat — Démonstrations du dernier théorème de Fermat Pierre de Fermat En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l équation diophantienne suivante, d inconnues x, y et z  …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”