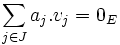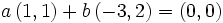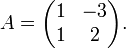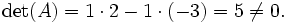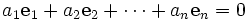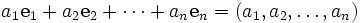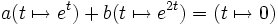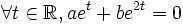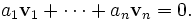- Indépendance Linéaire
-
Indépendance linéaire
En algèbre linéaire, étant donnée une famille de vecteurs, les vecteurs de la famille sont linéairement indépendants si toute combinaison linéaire finie nulle de ces vecteurs a nécessairement tous ses coefficients nuls. Cela revient à dire qu'aucun des vecteurs de la famille n'est combinaison linéaire finie des autres. Par exemple dans l'espace vectoriel euclidien
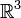 les trois vecteurs (1,0,0), (0,1,0) et (0,0,1) sont linéairement indépendants, tandis que (2, − 1,1), (1,0,1) et (3, − 1,2) ne sont pas linéairement indépendants. Dans le cas où des vecteurs ne sont pas linéairement indépendants, ils sont dits linéairement dépendants.
les trois vecteurs (1,0,0), (0,1,0) et (0,0,1) sont linéairement indépendants, tandis que (2, − 1,1), (1,0,1) et (3, − 1,2) ne sont pas linéairement indépendants. Dans le cas où des vecteurs ne sont pas linéairement indépendants, ils sont dits linéairement dépendants.Sommaire
Définitions
- Soient n un entier naturel non nul, et
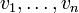 n vecteurs d'un espace vectoriel E sur un corps commutatif K. Les vecteurs sont dits linéairement indépendants si
n vecteurs d'un espace vectoriel E sur un corps commutatif K. Les vecteurs sont dits linéairement indépendants si
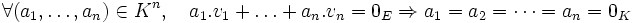 .
.
Autrement dit toute combinaison linéaire nulle des vecteurs
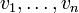 a nécessairement des coefficients tous nuls, c'est-à-dire que la seule combinaison linéaire nulle de ces vecteurs est la combinaison linéaire triviale.
a nécessairement des coefficients tous nuls, c'est-à-dire que la seule combinaison linéaire nulle de ces vecteurs est la combinaison linéaire triviale.La famille
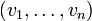 est alors dite libre.
est alors dite libre.Dans le cas contraire, les vecteurs sont dits linéairement dépendants et ainsi
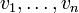 sont linéairement dépendants si par définition:
sont linéairement dépendants si par définition: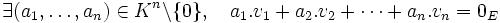 .
.
Cela signifie qu'il existe des scalaires non tous nuls tels que la combinaison linéaire de
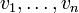 associée soit nulle.
associée soit nulle.Dans ce cas, la famille
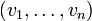 est dite liée.
est dite liée.Remarque: le zéro à droite est le vecteur nul, pas le zéro du corps.
- Soit E un K-espace vectoriel, et soit
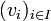 une famille de vecteurs de E. La famille est libre (ou les vecteurs de la famille sont linéairement indépendants) si pour toute famille finie
une famille de vecteurs de E. La famille est libre (ou les vecteurs de la famille sont linéairement indépendants) si pour toute famille finie 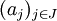 d'éléments de K dont l'ensemble d'indices J est inclus dans I,
d'éléments de K dont l'ensemble d'indices J est inclus dans I,
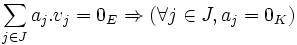 .
.
Soit E un K-espace vectoriel, et soit
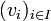 une famille de vecteurs de E. La famille est liée (ou les vecteurs de la famille sont linéairement dépendants) s'il existe une famille finie
une famille de vecteurs de E. La famille est liée (ou les vecteurs de la famille sont linéairement dépendants) s'il existe une famille finie 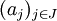 d'éléments de K non nuls telle que
d'éléments de K non nuls telle queoù l'ensemble d'indices J est un sous-ensemble fini non vide de I.
Nous définirions de même la notion de partie libre ou liée. Une partie A de E est alors libre si et seulement si la famille
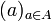 est libre et une partie A de E est liée si et seulement si la famille
est libre et une partie A de E est liée si et seulement si la famille 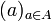 est liée.
est liée.Une famille est liée si et seulement si l'un de ses éléments appartient au sous-espace vectoriel engendré par les autres vecteurs de la famille.
Résultat important: Une partie libre de vecteurs d'un espace vectoriel forme une partie basique de l'espace vectoriel engendré par la partie.
Exemples
Exemple 1
Les vecteurs (1,1) et ( − 3,2) dans
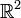 sont linéairement indépendants.
sont linéairement indépendants.Démonstration
Soit a et b deux nombres réels tels que
Alors
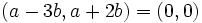 et
et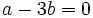 et
et 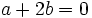 .
.
Ces deux relations nous donnent immédiatement a = 0 et b = 0.
Autre démonstration utilisant les déterminants
Une autre méthode utilise le fait que n vecteurs de
 sont linéairement dépendants si et seulement si le déterminant de la matrice obtenue en plaçant les composantes des vecteurs en colonne est nulle.
sont linéairement dépendants si et seulement si le déterminant de la matrice obtenue en plaçant les composantes des vecteurs en colonne est nulle.Dans ce cas, la matrice formées par les composantes des vecteurs s'écrit:
Le déterminant de cette matrice est:
Puisque le déterminant de cette matrice est non nul, les vecteurs (1,1) et ( − 3,2) sont linéairement indépendants. Cette méthode peut seulement être appliquée lorsque le nombre de vecteurs est égal au nombre de composantes des vecteurs.
Exemple 2
Soit
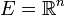 et considérons les éléments suivants de E:
et considérons les éléments suivants de E:Alors
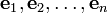 sont linéairement indépendants.
sont linéairement indépendants.Démonstration
Supposons que a1, a2, ..., an soient des réels tels que :
Donc
Et ainsi
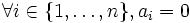 .
.
Exemple 3
Soit
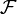 l'espace vectoriel de toutes les fonctions réelles d'une variable réelle.
l'espace vectoriel de toutes les fonctions réelles d'une variable réelle.Alors les fonctions
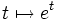 et
et 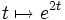 de
de 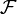 sont linéairement indépendantes.
sont linéairement indépendantes.Démonstration
Supposons que a et b soient des nombres réels tels que
Alors
Nous voulons montrer que a = 0 et b = 0;
Dans ce but, divisons pat et (qui n'est jamais nul) et soustrayons a pour obtenir:
En d'autres termes, la fonction
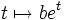 doit être constante, ce qui ne peut se produire que lorsque b = 0. Il s'ensuit que a est aussi nul.
doit être constante, ce qui ne peut se produire que lorsque b = 0. Il s'ensuit que a est aussi nul.Espace projectif des dépendances linéaires
Une relation de dépendance linéaire de n vecteurs
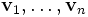 peut être représentée par un n-uplet
peut être représentée par un n-uplet 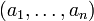 de n scalaires, non tous nuls, tels que
de n scalaires, non tous nuls, tels queSi une telle relation de dépendance linéaire existe, alors les n vecteurs sont linéairement dépendants. Il est alors possible d'identifier deux relations de dépendances linéaires si l'une est multiple non nul de l'autre relation, parce que dans ce cas les deux correspondent à la même dépendance linéaire des vecteurs entre eux. Sous, cette identification, l'ensemble des n-uplets décrivant les dépendances linéaires des vecteurs
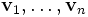 est un espace projectif.
est un espace projectif.Voir aussi
- L'orthogonalité
- Les matroïdes (paragraphe généralisation du concept)
- L'indépendance algébrique
- Portail des mathématiques
Catégorie : Espace vectoriel - Soient n un entier naturel non nul, et
Wikimedia Foundation. 2010.