Dodécaèdre Tronqué Parabiaugmenté

Dodécaèdre Tronqué Parabiaugmenté

Dodécaèdre tronqué parabiaugmenté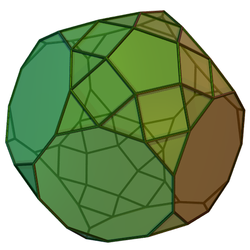

 Dodécaèdre tronqué parabiaugmenté
Parabiaugmented truncated dodecahedron.png
Type
dodécaèdre tronqué augmenté
J68 - J69 - J70
Sommets
70
Arêtes
120
Faces
52
30 t 10 c 2 p 10 d
Configuration faciale
-
Groupe symétrique
D5d
Dual
-
Propriétés
convexe

Le dodécaèdre tronqué parabiaugmenté est un polyèdre faisant partie des solides de Johnson (J68). Comme le nom l'indique, il peut être construit en augmentant un dodécaèdre tronqué sur deux faces décagonales opposées par deux coupoles décagonales (J5).

Les 92 solides de Johnson ont été nommés et décrits par Norman Johnson en 1966.

Liens externes


Solides géométriques
Les polyèdres
Les solides de Platon
Tétraèdre - Cube - Octaèdre - Icosaèdre - Dodécaèdre
Les solides d'Archimède
Tétraèdre tronqué - Cube tronqué - Octaèdre tronqué - Dodécaèdre tronqué - Icosaèdre tronqué - Cuboctaèdre - Cube adouci - Icosidodécaèdre - Dodécaèdre adouci - Petit rhombicuboctaèdre - Grand rhombicuboctaèdre - Petit rhombicosidodécaèdre - Grand rhombicosidodécaèdre
Les solides de Kepler-Poinsot
Petit dodécaèdre étoilé - Grand dodécaèdre étoilé - Grand dodécaèdre - Grand icosaèdre
Les solides de Catalan
Triakioctaèdre - Tétrakihexaèdre - Triakitétraèdre - Pentakidodécaèdre - Triaki-icosaèdre - Dodécaèdre rhombique - Icositétraèdre pentagonal - Triacontaèdre rhombique - Hexacontaèdre pentagonal - Icositétraèdre trapézoïdal - Hexakioctaèdre - Hexacontaèdre trapézoïdal - Hexaki icosaèdre
Les solides de Johnson
Les solides de révolution
Boule - Cylindre de révolution - Cône de révolution - Tore - Paraboloïde de révolution
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Dod%C3%A9ca%C3%A8dre tronqu%C3%A9 parabiaugment%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dodécaèdre Tronqué Parabiaugmenté de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”