Vecteur propre généralisé
- Vecteur propre généralisé
-
Sous-espace caractéristique
Définitions
Soient E un K-espace vectoriel de dimension finie et u un endomorphisme de E. Soit 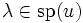
- on appelle sous-espace caractéristique, sous-espace spectral, ou encore espace propre généralisé de
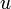 associé à la valeur propre
associé à la valeur propre 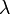 le sous espace :
le sous espace : ![N_{\lambda}(u) = \ker\left[ (u- \lambda Id)^m \right]](/pictures/frwiki/101/e8224cadd4f26ac338a0b4b62fb6e616.png) , Id étant l'application identité et m la multiplicité de λ dans le polynôme caractéristique de l'endomorphisme u.
, Id étant l'application identité et m la multiplicité de λ dans le polynôme caractéristique de l'endomorphisme u.
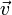 est un vecteur propre généralisé de u associé à la valeur propre λ s'il existe
est un vecteur propre généralisé de u associé à la valeur propre λ s'il existe 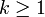 tel que
tel que 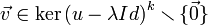
Remarque : Cette définition implique que 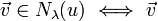 est un vecteur propre généralisé de u associé à λ.
est un vecteur propre généralisé de u associé à λ.
Intérêt
Les sous-espaces caractéristiques sont utilisés dans la caractérisation de la trigonalisation d'un endomorphisme. En effet un endomorphisme u d'un espace vectoriel E est trigonalisable si et seulement si E est la somme (directe) des sous-espaces caractéristiques de u, c'est-à-dire si et seulement si il existe une base de E formée de vecteurs propres généralisés de u. Cette caractérisation rejoint celle donnée à l'aide du polynôme caractéristique qui doit être scindé pour que l'endomorphisme soit trigonalisable.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Application linéaire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Vecteur propre généralisé de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace propre généralisé — Sous espace caractéristique Définitions Soient E un K espace vectoriel de dimension finie et u un endomorphisme de E. Soit on appelle sous espace caractéristique, sous espace spectral, ou encore espace propre généralisé de associé à la valeur… … Wikipédia en Français
Espace propre généralisé et vecteurs propres — Sous espace caractéristique Définitions Soient E un K espace vectoriel de dimension finie et u un endomorphisme de E. Soit on appelle sous espace caractéristique, sous espace spectral, ou encore espace propre généralisé de associé à la valeur… … Wikipédia en Français
Valeur propre, vecteur propre et espace propre — Fig. 1. A étire le vecteur x sans changer sa direction. x est un vecteur propre pour A, pour la valeur propre λ. En mathématiques, et plus particulièrement en algèbre linéaire, le concept de vecteur propre est une notion algébrique s appliquant à … Wikipédia en Français
Vecteur — Pour les articles homonymes, voir Vecteur (homonymie). Deux vecteurs et et le vecteur somme. En … Wikipédia en Français
Vecteur axial — Pseudovecteur En physique et en mathématiques, un pseudovecteur ou vecteur axial est un objet mathématique qui se comporte de la même manière qu un vecteur pour une rotation directe (conservant les angles orientés) mais qui change de sens lors d… … Wikipédia en Français
Problème aux valeurs propres généralisé — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Base propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Sous-espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… … Wikipédia en Français
Pseudo-vecteur — Pseudovecteur En physique et en mathématiques, un pseudovecteur ou vecteur axial est un objet mathématique qui se comporte de même manière qu un vecteur pour une rotation directe (conservant les angles orientés), mais qui change de sens lors d… … Wikipédia en Français
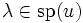
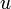 associé à la valeur propre
associé à la valeur propre 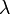 le sous espace :
le sous espace : ![N_{\lambda}(u) = \ker\left[ (u- \lambda Id)^m \right]](/pictures/frwiki/101/e8224cadd4f26ac338a0b4b62fb6e616.png) , Id étant l'application identité et m la multiplicité de λ dans le polynôme caractéristique de l'endomorphisme u.
, Id étant l'application identité et m la multiplicité de λ dans le polynôme caractéristique de l'endomorphisme u.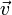 est un vecteur propre généralisé de u associé à la valeur propre λ s'il existe
est un vecteur propre généralisé de u associé à la valeur propre λ s'il existe 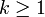 tel que
tel que 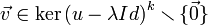
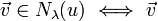 est un vecteur propre généralisé de u associé à λ.
est un vecteur propre généralisé de u associé à λ.
