- Rotonde pentagonale allongée
-
Rotonde décagonale allongée
Rotonde décagonale allongée 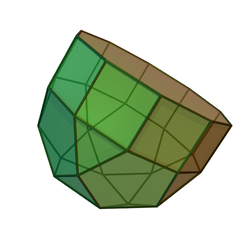
Type Rotonde allongée
J20 - J21 - J22Sommets 30 Arêtes 55 Faces 27 10 t 10 c 6 p 1 d Configuration faciale - Groupe symétrique C5v Dual - Propriétés convexe En géométrie, la rotonde décagonale allongée est un des solides de Johnson (J21). Comme son nom l'indique, il peut être construit par allongement d'une rotonde décagonale (J6), c'est-à-dire en attachant un prisme décagonal à sa base. Il peut aussi être vu comme une orthobirotonde décagonale allongée (J42) dont on a enlevé une rotonde décagonale.
Les 92 solides de Johnson ont été nommés et décrits par Norman Johnson en 1966.
Lien externe
- Portail de la géométrie
Catégorie : Solide de Johnson
Wikimedia Foundation. 2010.
