Polytope convexe

Ensemble convexe

Pour les autres sens du mot « convexe », voir convexité.

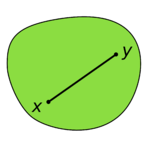
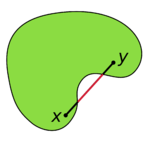
Un objet géométrique est dit convexe lorsque, chaque fois qu'on y prend deux points $A$ et $B$ , le segment $[A, B]$ qui les joint y est entièrement contenu. Ainsi un cube plein, un disque ou une boule sont convexes, mais un objet creux ou bosselé ne l'est pas.

Sommaire

1 Définition
- 1.1 Exemples
2 Propriétés élémentaires et outils fondamentaux
3 Propriétés topologiques
4 Ensembles convexes et géométrie combinatoire
- 4.1 Polytopes
- 4.2 Les théorèmes de Radon, Helly et Carathéodory
5 Références
6 Bibliographie

Définition

Une partie convexe.

Une partie non convexe.

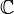On suppose travailler dans un contexte où le segment $[x, y]$ reliant deux points quelconques $x$ et $y$ a un sens (par exemple dans un espace affine sur $\R$ ou sur $\mathbb{C}\!\!\!$ , ou dans un espace hyperbolique).

Définition — Un ensemble $C$ est dit convexe lorsque, pour tout $x$ et $y$ de $C$ , le segment $[x, y]$ est tout entier contenu dans $C$ .

Sauf précision explicite, tout ce qui suit concerne le seul contexte des convexes dans des espaces affines (ou vectoriels).

On appellera dimension du convexe non vide $C$ la dimension du sous-espace affine engendré par $C$ .

Exemples

Les sous-ensembles convexes de $\R$ des nombres réels sont les intervalles de $\ \R$ .

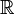Dans un espace affine, tout sous-espace affine est convexe ; c'est en particulier le cas des sous-espaces vectoriels des espaces vectoriels.

Dans un espace vectoriel normé (réel ou complexe), toute boule est convexe, qu'il s'agisse d'une boule ouverte ou d'une boule fermée.

Propriétés élémentaires et outils fondamentaux

Intersections de convexes

L'intersection de deux convexes (et même d'une famille quelconque de convexes) est elle-même convexe^[1] (et ce très généralement, dès lors qu'on peut définir la convexité).

Stabilité par barycentres à coefficients positifs

La définition de la convexité fait intervenir le choix de deux points quelconques $x$ et $y$ , puis la considération des points du segment $[x, y]$ , autrement dit des barycentres à coefficients positifs de ces deux points. En utilisant le théorème d'associativité des barycentres, on voit sans mal que cela n'aurait rien changé de considérer des barycentres à coefficients positifs d'un nombre quelconque de points. Précisément on a^[2] :

Proposition — Un sous-ensemble $C$ d'un espace affine $E$ est convexe si et seulement si pour toute famille finie $(x 1,..., x k)$ de points de $C$ et tout choix $(λ 1,...,λ k)$ de coefficients positifs, le barycentre des $(x i)$ affublés des poids $(λ i)$ est lui-même dans $C$ .

Enveloppe convexe

Article détaillé : Enveloppe convexe.

Étant donnée une partie quelconque $A$ de l'espace ambiant $E$ (espace affine ou contexte plus général), il existe au moins un sous-ensemble convexe de $E$ contenant $A$ , à savoir $E$ lui-même ; ceci autorise à considérer l'intersection de tous les sous-ensembles convexes de $E$ contenant $A$ . On l'appelle l'enveloppe convexe de $A$ .

On vérifie aussitôt que c'est donc le plus petit sous-ensemble convexe de $E$ contenant $A$ , au sens de l'inclusion sur $P (E)$ . Si $x$ et $y$ sont deux points de $E$ , l'enveloppe convexe de l'ensemble ${x, y}$ est le segment $[x, y]$ .

Le théorème de la projection

Article détaillé : Théorème de projection sur un convexe fermé.

À condition d'être en train de travailler dans un espace euclidien (ou plus généralement dans un espace de Hilbert), on dispose d'un résultat remarquable : étant donné un convexe fermé, pour tout point $x$ de l'espace, il existe un et un seul point $p (x)$ du convexe à distance minimale de $x$ . Ce résultat est accompagné de diverses informations complémentaires, notamment le caractère obtus de l'angle 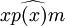$\widehat{xp(x)m}$ pour tout point $m$ du convexe, ou le caractère 1-lipschitzien de l'application $p$ .

Séparation des convexes et structure de la frontière

Articles détaillés : Séparation des convexes et Points et parties remarquables de la frontière d'un convexe.

Une technique utile est celle de la « séparation » de deux convexes. Elle consiste, étant donné deux convexes sans point commun d'un même espace, à découper cet espace en deux par un hyperplan (un plan en dimension 3) qui laisse les convexes de part et d'autre de ce mur de séparation. Les démonstrations de la possibilité d'un tel découpage sont multiples, permettant d'obtenir des énoncés plus ou moins généraux ; certaines utilisent le théorème de Hahn-Banach, outil d'analyse fonctionnelle particulièrement pertinent pour l'étude en dimension infinie.

Cette méthode permet tout particulièrement de justifier de l'existence en chaque point de la frontière d'un convexe d'un « hyperplan d'appui » : un hyperplan passant par ce point et laissant le convexe tout entier dans l'un des deux demi-espaces qu'il borde. Ce résultat est à son tour fondamental pour étudier plus en détail la structure de la frontière des convexes (divisions en faces, arêtes, etc...) et particulièrement des polyèdres convexes. On est ainsi amenés à distinguer diverses catégories de points (points extrémaux, sommets) qui joueront un rôle central dans les problèmes d'optimisation sur le convexe, par exemple en programmation linéaire.

Fonctions convexes associées à un ensemble convexe

L'étude des ensembles convexes peut bénéficier des résultats d'analyse qui concernent les fonction convexes. Plusieurs telles fonctions peuvent en effet être associées à un convexe non vide $C$ .

La plus simple est sa fonction indicatrice, variante de la fonction caractéristique adaptée à la convexité : c'est la fonction qui prend la valeur $0$ sur $C$ , et la valeur $+\infty$ en dehors :

Lorsque l'espace ambiant est un espace vectoriel de dimension finie, muni d'une structure euclidienne, on peut ensuite considérer la fonction convexe conjuguée de la précédente, qu'on appelle alors la fonction d'appui de $C$ ;

Enfin, relativement à chacun des points de $C$ , on peut définir la jauge du convexe, qui est reliée de façon très parlante à sa géométrie et utile notamment dans certaines preuves des théorèmes de séparation des convexes.

Article détaillé : Jauge (mathématiques).

Propriétés topologiques

Dans cette section, on suppose l'espace ambiant muni d'une topologie compatible avec sa structure géométrique (c'est toujours le cas dans les espaces de dimension finie ; si on est dans un espace vectoriel de dimension infinie cela revient à exiger qu'il s'agisse d'un espace vectoriel topologique).

Adhérence, intérieur, frontière

Article détaillé : Adhérence, intérieur et frontière d'un convexe.

Les opérateurs d'adhérence et d'intérieur préservent la convexité. En outre, lorsque le convexe considéré n'est pas d'intérieur vide (et on peut facilement se ramener à ce cas en le considérant comme partie de son enveloppe affine et non de l'espace global), le convexe, son intérieur et son adhérence ont tous trois la même frontière.

On peut montrer très facilement qu'un convexe compact est l'enveloppe convexe de sa frontière (hors le cas dégénéré de la dimension 0).

Connexité

Une partie convexe est évidemment connexe par arcs donc connexe.

Description à homéomorphisme près en dimension finie

Pour 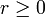$r\geq 0$ , on notera $B r$ la boule euclidienne fermée de centre $0$ et de rayon $1$ dans $\R^r$ .

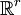Les compacts convexes disposent d'une structure simple :

Théorème — Soit $C$ un convexe compact de 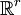$\R^r$ , il existe un entier positif $d$ , plus petit ou égal à $r$ tel que $C$ soit homéomorphe à $B d$ .

Les convexes fermés d'une dimension finie $d$ donnée sont homéomorphes à l'un ou l'autre d'un nombre limité ( $d + 2$ ) de modèles simples.

Théorème — Soit 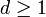$d\geq 1$ et soit $C$ un convexe de dimension $d$ , fermé dans son espace ambiant. Alors :

soit il existe $r$ avec 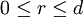$0\leq r\leq d$ tel que $C$ soit homéomorphe à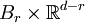 $B_r\times \R^{d-r}$

soit $C$ est homéomorphe à un demi-espace fermé dans $\R^d$ .

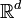Dans tous les cas, l'homéomorphisme envoie la frontière relative de $C$ sur la frontière relative du modèle.

Pour lire ce théorème sur un exemple instructif, celui de la dimension $3$ , les convexes fermés de dimension $3$ sont homéomorphes à un des cinq modèles suivants : 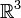$\R^3$ tout entier, la région délimitée par deux plans parallèles, un cylindre, une boule dans 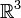$\R^3$ ou un demi-espace.

Les intérieurs relatifs de tous les modèles énumérés au théorème précédent sont homéomorphes entre eux, c'est-à-dire homémorphes à 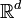$\R^d$ . L'homéomorphisme donné par le théorème précédent échangeant les intérieurs relatifs, on peut donc en conclure que tous les ouverts convexes de dimension $d$ sont homéomorphes entre eux (ce qui, en réalité, était une étape de la preuve). On peut en fait obtenir mieux, à savoir un difféomorphisme.

Théorème — Soit 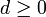$d\geq 0$ et soit $C$ un convexe de dimension $d$ , ouvert dans son espace ambiant. Alors :

$C$ est difféomorphe à $\R^d$ .

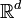Il ne faut pas espérer une classification aussi simple des convexes sans condition topologique : qu'on songe que pour toute partie $A$ du cercle-unité de 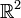$\R^2$ l'ensemble obtenu en réunissant le disque-unité ouvert et $A$ est convexe^[3]

Démonstrations

Il existe un entier d tel que le convexe compact C de R^r soit homéomorphe à la boule fermée B_d :

Une translation est un homéomorphisme, il suffit de montrer la proposition pour un translaté de C. On peut donc supposer, sans perte de généralité que C contienne le vecteur nul. Soit F le sous-espace vectoriel de Rⁿ engendré par C.

Le convexe C, considéré comme un sous-ensemble de F, est d'intérieur non nul.

Comme, pour un espace vectoriel réel de dimension finie, toutes les normes sont équivalentes^[4], on peut choisir celle pour laquelle la démonstration est la plus simple. Soit (e_j) un ensemble de vecteurs de C définissant une base de F. On choisit pour norme, celle qui à un vecteur associe la valeur absolue de sa plus grande coordonnée dans la base (e_j). Pour cette norme on remarque que la boule de centre 1/(2d) (Σe_j) et de rayon 1/2d est formé des vecteurs ayant des coordonnées positives et inférieures à 1/d dans la base (e_j). Ces vecteurs sont tous des éléments de C. Ce qui montre que le centre de la boule est bien dans l'intérieur recherché.

On considère maintenant uniquement l'espace vectoriel F et on note d sa dimension. Quitte à opérer une nouvelle translation, on peut toujours supposer que le vecteur nul est dans l'intérieur de C. On note B la boule fermée de centre le vecteur nul et de rayon 1 et S la sphère de même centre et de même rayon. Soit u un vecteur de S et E_λ(u) l'ensemble des réels positifs λ tels que λu soit élément de C. Comme C est compact, l'ensemble est borné et l'ensemble E_λ(u) l'est aussi. Soit φ(u) la borne supérieure de E_λ(u). On vient de définir une application de S dans R₊ qui à u associe φ(u). Comme il existe un voisinage du vecteur nul inclus dans C, la fonction φ ne s'approche jamais de la valeur 0.

L'application φ est continue.

Supposons qu'il existe un point u de S tel que φ ne soit pas continue en u. Il existe alors un réel strictement positif

μ

strictement plus petit que φ(u) tel que :

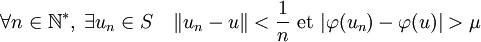
$\forall n \in \N^*,\; \exists u_n \in S \quad \|u_n - u \| < \frac 1n \text { et } |\varphi(u_n) - \varphi (u)| > \mu$

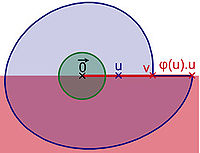
La suite (φ(u_n) est positive et bornée, elle est à valeurs dans un compact et il existe une sous-suite convergente (φ(u_ψ(n)), d'après le théorème de Bolzano-Weierstrass. Soit λ_l la limite de cette suite. La suite (φ(u_ψ(n)).u_ψ(n)) est une suite de points de la frontière de C, convergeant vers λ_l.u. Le point v = λ_l.u est un point de la frontière de C et la distance entre les deux points de la frontière de C φ(u).u et v est supérieur à μ. Comme φ(u) est la plus grande valeur telle que φ(u).u soit un élément de C, λ_l est strictement plus petit que φ(u) et par construction il est strictement plus grand que 0. Il ne peut valoir 0 car le vecteur nul n'est pas un point de la frontière de C et λ_l.u l'est. Comme v est un point qui n'est pas dans l'intérieur de C, Il existe un hyperplan d'appui passant par v séparant l'espace en deux composantes connexes, dont l'une contient l'intérieur du compact C (en rouge sur la figure de droite). Cet hyperplan contient la droite passant par le vecteur nul, v et φ(u).u. Cet hyperplan possède une intersection non vide avec le voisinage du vecteur nul strictement inclus dans C (en vert sur la figure). Cette contradiction montre que la fonction φ est continue.

La proposition précédente permet simplement de démontrer le résultat du paragraphe.

Le convexe compact C est homéomorphe à la boule B.

On considère l'application de B dans C, qui à u associe φ(u).u, si u est différent du vecteur nul et qui laisse invariant le vecteur nul. Cette application est continue pour tout vecteur non nul. Comme l'application φ est borné (car C est un compact) elle est aussi continue au vecteur nul. L'application φ est bijective. Comme φ(u) n'est jamais nul (si u ne l'est pas), l'application inverse est celle qui, à u différent du vecteur nul, associe φ(u)^-1.u et au vecteur nul encore le vecteur nul. L'application considérée est bien un homéomorphisme, ce qui termine la démonstration.

Ensembles convexes et géométrie combinatoire

Les ensembles convexes jouent un rôle central en géométrie combinatoire, ne serait-ce que parce que, face à un nombre fini de points d'un espace affine, l'opération géométrique la plus évidente qu'on puisse leur appliquer est d'examiner leur enveloppe convexe : ce qu'on appelle un polytope.

Polytopes

Article détaillé : Polytope.

L'objet de base de la géométrie combinatoire convexe, c'est le polytope, qu'on peut définir comme enveloppe convexe d'un nombre fini de points.

Pour ne citer ici que l'exemple sans doute le plus fameux de résultat de géométrie combinatoire, en dimension 3, les nombres de sommets, d'arêtes et de faces d'un polytope sont liés par la formule d'Euler (voir à ce sujet l'article Caractéristique d'Euler) :

$S - A + F = 2\,\!$ .

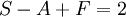Les théorèmes de Radon, Helly et Carathéodory

Articles détaillés : Théorème de Radon (géométrie), Théorème de Helly et Théorème de Carathéodory (géométrie).

Considérons un ensemble 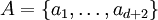$A = \{a_1, \dots, a_{d+2}\}$ de $d + 2$ points dans un espace affine de dimension $d$ .

Le théorème de Radon affirme que :

Théorème (Radon) — $A$ admet une partition en deux parties $A 1, A 2$ dont les enveloppes convexes $Conv(A 1)$ et $Conv(A 2)$ se rencontrent.

Pour énoncer de façon parallèle les théorèmes de Helly et Carathéodory, on va introduire une notation : pour chaque indice $i$ variant entre $1$ et $d + 2$ , notons 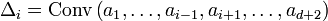$\Delta_i=\mathrm{Conv}\left(a_1, \dots, a_{i-1}, a_{i+1}, \ldots, a_{d+2}\right)$ l'enveloppe convexe des points de $A$ autres que le point $a i$ . En dimension $2$ , chaque $Δ i$ serait un triangle (et il y en aurait quatre) ; en dimension $3$ on aurait affaire à une collection de cinq tétraèdres, et ainsi de suite.

Les deux énoncés suivants sont des cas particuliers des énoncés les plus courants des théorèmes de Helly et Carathéodory, mais qui en contiennent essentiellement toute l'information : on reconstitue facilement les énoncés généraux à partir des versions fournies ci-dessous.

Théorème (Helly) — Il existe un point commun aux $d + 2$ simplexes $Δ i$ .

Théorème (Carathéodory) — Les $d + 2$ simplexes $Δ i$ recouvrent tout le polytope enveloppe convexe de $A$ .

Ces théorèmes sont étroitement liés : la démonstration la plus courante de Helly est fondée sur Radon, tandis qu'on prouve facilement Carathéodory indépendamment, mais il est aussi possible par exemple de déduire Helly de Carathéodory ou le contraire.

D'innombrables variantes les précisent ou les généralisent.

Références

Dans les sections renvoyant à un article détaillé, on se réfèrera à cet article détaillé pour les sources à l'appui des informations qui y figurent.

Les références à un auteur sans mention d'ouvrage renvoient au livre de cet auteur mentionné en bibliographie.

↑ Eggleston, Th. 1, p. 8. (Le résultat est énoncé dans 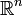$\R^n$ dans cette source, mais la preuve s'adapte évidemment à une situation plus générale).
↑ Eggleston p. 4-5. (Le résultat est énoncé dans 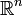$\R^n$ dans cette source, mais la preuve s'adapte évidemment à une situation plus générale).
↑ L'ensemble de cette sous-section est issu de Marcel Berger, Géométrie [détail des éditions], section II-3, tome 3, p. 29-38 dans l'édition de 1978.
↑ Les détails sont donnés dans l'article Topologie d'un espace vectoriel de dimension finie.

Bibliographie

Marcel Berger, Géométrie [détail des éditions]
(en) H.G. Eggleston, Convexity, Cambridge University Press, coll. « Tracts in Mathematics and Mathematical Physics » n° 47, 1958, réimpression avec corrections 1969.

Articles en rapport avec la convexité
Géométrie convexe	Article principal : Ensemble convexe Outils et résultats fondamentaux : Enveloppe convexe • Adhérence, intérieur et frontière d'un convexe • Projection sur un convexe fermé • Séparation des convexes • Points remarquables à la frontière d'un convexe • Polytope • Théorème de Krein-Milman • Lemme de Farkas Géométrie combinatoire : Théorème de Carathéodory • Théorème de Radon • Théorème de Helly Géométrie métrique : Courbe de largeur constante • Théorème des quatre sommets Algorithmes de géométrie convexe : Approche polyèdrale • Marche de Jarvis • Parcours de Graham • Théorème optimisation/séparation Optimisation linéaire : Programmation linéaire • Algorithme du simplexe • Génération de colonnes
Interactions géométrie-analyse	Théorème de Hahn-Banach • Jauge
Analyse convexe	Article principal : Fonction convexe Outils et résultats fondamentaux : Inégalité de Jensen Optimisation convexe : Conditions de Kuhn-Tucker • Méthode du point intérieur
Utilisations de la convexité	Inégalités de convexité : Inégalité arithmético-géométrique • Inégalité de Hölder Analyse fonctionnelle : Espace localement convexe • Théorème du point fixe de Schauder Localisation de zéros de polynômes : Théorème de Gauss-Lucas Théorie des nombres : Théorème de Minkowski

Portail de la géométrie

Ce document provient de « Ensemble convexe ».

Catégorie : Géométrie convexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Polytope convexe de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Polytope — Un polytope en dimension 3 Le terme polytope admet plusieurs définitions au sein des mathématiques. Principalement car les usages diffèrent en quelques points selon les pays, mais l usage américain ayant tendance à s imposer, on se retrouve… … Wikipédia en Français
Polytope regulier — Polytope régulier Pour les articles homonymes, voir régulier. Le Dodécaèdre, un des cinq solides platoniciens. E … Wikipédia en Français
Polytope régulier — Pour les articles homonymes, voir régulier. Le dodécaèdre régulier, un des cinq solides platoniciens. En mathématiques, plus précisément … Wikipédia en Français
Polytope des stables — Un stable est un ensemble de sommets deux à deux non adjacents. Le polytope des stables de G est l enveloppe convexe des fonctions caractéristiques de ses stables. Plus précisément, soit G un graphe à n sommets. Un choix de numérotation fait… … Wikipédia en Français
Polytope croisé — Octaèdre Octaèdre Type Polyèdre régulier Faces Triangle Éléments : · Faces · Arêtes · Sommets · Caractéristique 8 12 6 2 Faces par sommet 4 Sommets par face … Wikipédia en Français
Ensemble convexe — Pour les autres sens du mot « convexe », voir convexité. Un objet géométrique est dit convexe lorsque, chaque fois qu on y prend deux points A et B, le segment [A,B] qui les joint y est entièrement contenu. Ainsi un cube plein, un… … Wikipédia en Français
Polyèdre convexe — Ensemble convexe Pour les autres sens du mot « convexe », voir convexité. Un objet géométrique est dit convexe lorsque, chaque fois qu on y prend deux points A et B, le segment [A,B] qui les joint y est entièrement contenu. Ainsi… … Wikipédia en Français
Fonction convexe — Fonction convexe. En mathématiques une fonction convexe est une fonction réelle d une variable réelle définie sur un intervalle et dont le graphe est « tourné vers le haut » : pour tous points A et B de ce graphe, le segment [AB]… … Wikipédia en Français
Fonction Convexe — En mathématiques, et plus particulièrement en analyse, une fonction convexe est une fonction numérique vérifiant une propriété de sous additivité vis à vis de la barycentration. Graphiquement, cela correspond à un graphe dont la « partie… … Wikipédia en Français
4-polytope régulier convexe — Un hypercube en rotation En mathématique, un polytope régulier convexe à 4 dimensions (ou polychore) est un polytope à 4 dimensions qui est à la fois régulier et convexe. Ce sont les analogues en 4 dimensions des solides de Platon (3 dimensions)… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Polytope convexe

Ensemble convexe

Sommaire