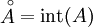- Intérieur (mathématiques)
-
Intérieur (topologie)
 Pour les articles homonymes, voir intérieur.
Pour les articles homonymes, voir intérieur.En mathématiques, l'intérieur est une notion de topologie appliquée à une partie d'un espace topologique ou à une variété à bord.
Dans le premier cas, l'intérieur d'une partie est sa plus grande sous-partie ouverte. Il est constitué des points de cette partie qui ne « touchent » pas le complémentaire, au sens où ils admettent un voisinage qui en est disjoint.
Cette définition s'applique en particulier aux parties d'espace métrique ou d'espace euclidien.L'intérieur d'une variété à bord est défini comme le complémentaire du bord. Dans ce cas il est intrinsèque, au sens où il ne dépend pas d'un plongement de la variété dans un espace plus grand. Cependant, les deux définitions coïncident pour une variété compacte plongée en codimension zéro.
Dans les deux cas, l'intérieur se note soit à l'aide d'un petit cercle suscrit, soit par une notation préfixe avec l'abréviation int :
Sommaire
Topologie générale
Constructions équivalentes
La définition de l'intérieur d'une partie comme la plus grande sous-partie ouverte nécessite une démonstration de son existence.
La réunion de tous les ouverts inclus dans une partie forme elle-même un ouvert inclus dans cette partie. Par construction, elle inclut tous les autres, c'est donc une construction de l'intérieur de la partie.
Il est aussi possible de définir les points intérieurs d'une partie comme les points dont la partie est un voisinage. Tous ces points intérieurs appartiennent donc à des ouverts inclus dans la partie donc appartiennent à l'intérieur. Réciproquement, l'intérieur est un voisinage de tous ses points donc ne contient que des points intérieurs. Finalement, l'intérieur peut aussi se définir comme l'ensemble des points intérieurs.
Propriétés
- Une partie est ouverte si et seulement si elle est égale à son intérieur ;
- idempotence : l'intérieur de l'intérieur est égal à l'intérieur ;
- croissance pour l'inclusion : si A est une sous-partie de B alors int(A) est une sous-partie de int(B).
Exemples
- Dans n'importe quel espace topologique, l'intérieur de l'ensemble vide est l'ensemble vide.
- Dans l'espace euclidien R des nombres réels muni de la topologie usuelle :
- l'intérieur du segment [0, 1] est l'intervalle ouvert ]0, 1[ ;
- l'intérieur de l'ensemble Q des nombres rationnels est vide.
- Dans l'espace des nombres complexes, alors l'intérieur de l'ensemble {z ∊ C / |z| ≥ 1} est l'ensemble {z ∊ C / |z| > 1}.
- Dans tout espace euclidien, l'intérieur d'un ensemble fini est l'ensemble vide.
- Dans une espace discret où toute partie est ouverte, toute partie est son propre intérieur.
- Dans un espace muni de la topologie grossière où les seuls ouverts sont l'espace total et l'ensemble vide, toute partie stricte est d'intérieur vide.
L'intérieur d'une partie dépend de la topologie considérée. Dans le cas de R :
- muni de la topologie de la limite inférieure, int([0, 1]) = [0, 1)[réf. nécessaire].
- muni de la topologie discrète, int([0, 1]) = [0, 1].
- muni de la topologie grossière int([0, 1]) est l'ensemble vide.
Voir aussi
- Portail des mathématiques
Catégorie : Topologie générale
Wikimedia Foundation. 2010.