Méthode des éléments finis

Pour les articles homonymes, voir Élément.

Solution bidimensionnelle d'une équation magnétostatique obtenue par éléments finis (les lignes donnent la direction du champ et la couleur son intensité)

Maillage utilisé pour l'image du haut (le maillage est plus resserré autour de la zone d'intérêt)

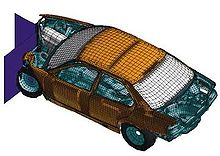Simulation numérique d'un Essai de choc sur une voiture: les cellules utilisées pour le maillage sont visibles sur la surface du véhicule.

En analyse numérique, la méthode des éléments finis est utilisée pour résoudre numériquement des équations aux dérivées partielles. Celles-ci peuvent par exemple représenter analytiquement le comportement dynamique de certains systèmes physiques (mécaniques, thermodynamiques, acoustiques, etc.).

Concrètement, cela permet par exemple de calculer numériquement le comportement d'objets même très complexes, à condition qu'ils soient continus et décrits par une équation aux dérivées partielles linéaire : mouvement d'une corde secouée par l'un de ses bouts, comportement d'un fluide arrivant à grande vitesse sur un obstacle, déformation d'une structure métallique, etc.

Introduction

La méthode des éléments finis fait partie des outils de mathématiques appliquées. Il s'agit de mettre en place, à l'aide des principes hérités de la formulation variationnelle ou formulation faible, un algorithme discret mathématique permettant de rechercher une solution approchée d’une équation aux dérivées partielles (ou EDP) sur un domaine compact avec conditions aux bords et/ou dans l'intérieur du compact. On parle couramment de conditions de type Dirichlet (valeurs aux bords) ou Neumann (gradients aux bords) ou de Robin (relation gradient/valeurs sur le bord).

Il s'agit donc avant tout de la résolution approchée d'un problème, où, grâce à la formulation variationnelle, les solutions du problème vérifient des conditions d'existence plus faibles que celles des solutions du problème de départ et où une discrétisation permet de trouver une solution approchée. Comme de nombreuses autres méthodes numériques, outre l'algorithme de résolution en soi, se posent les questions de qualité de la discrétisation :

existence de solutions,
unicité de la solution,
stabilité,
convergence,
et bien sûr : mesure d'erreur entre une solution discrète et une solution unique du problème initial.

La partie 2 va présenter le cadre général de la méthode des éléments finis, ainsi que le cas pratique le plus courant considérant des équations aux dérivées partielles linéaires dont on cherche une approximation par des fonctions affines.

La présentation en partie 3 est essentiellement physique, notamment mécanique. Elle ne doit être considérée que comme une présentation des éléments constitutifs de la modélisation discrète utilisée en résistance des matériaux via la méthode des éléments finis. C'est une approche tout à fait valide, un bon exemple pédagogique. Elle apporte un biais certain quant à une approche plus générale, du fait notamment de la linéarité supposée des matériaux.

Méthode des éléments finis

Principe général

La méthode des éléments finis permet donc de résoudre de manière discrète une EDP dont on cherche une solution approchée « suffisamment » fiable. De manière générale, cette EDP porte sur une fonction u, définie sur un domaine. Elle comporte des conditions aux bords permettant d'assurer existence et unicité d'une solution.

Sauf cas particuliers, la discrétisation passe par une redéfinition et une approximation de la géométrie, on considère donc le problème posé sur la géométrie approchée par un domaine polygonal ou polyédrique par morceaux. Une fois la géométrie approchée, il faut choisir un espace d'approximation de la solution du problème, dans la MEF, cet espace est défini à l'aide du maillage du domaine (ce qui explique aussi pourquoi il est nécessaire d'approcher la géométrie). Le maillage du domaine permet d'en définir un pavage dont les pavés sont les éléments finis. Un élément fini est la donnée d'une cellule élémentaire et de fonctions de base de l'espace d'approximation dont le support est l'élément, et définies de manière à être interpolantes (voir Fonctions de base).

Bien qu'il existe de nombreux logiciels exploitant cette méthode et permettant de « résoudre » des problèmes dans divers domaines, il est important que l'utilisateur ait une bonne idée de ce qu'il fait, notamment quant au choix du maillage et du type d'éléments qui doivent être adaptés au problème posé : aucun logiciel ne fera tout pour l'utilisateur, et il faut toujours garder un œil critique vis-à-vis de solutions approchées. Pour cela il existe des indicateurs d'erreur et des estimateurs d'erreur qui permettent d'ajuster les différents paramètres.

La solution trouvée, il reste cependant à déterminer les caractéristiques de la méthode ainsi développée, notamment l'unicité de l'éventuelle solution ou encore la stabilité numérique du schéma de résolution. Il est essentiel de trouver une estimation juste de l'erreur liée à la discrétisation et montrer que la méthode ainsi écrite converge, c’est-à-dire que l'erreur tend vers 0 si la finesse du maillage tend elle aussi vers 0.

Dans le cas d'une EDP linéaire avec opérateur symétrique (comme l'est l'opérateur laplacien), il s'agit finalement de résoudre une équation algébrique linéaire, inversible dans le meilleur des cas.

Dimensions

On développe ici la méthode des éléments finis en deux dimensions à valeurs réelles. On suppose que les équations étudiées sont des équations différentielles d'ordre deux.

La méthode est généralisable à des cadres d'espaces de dimension différente ou pour des équations aux dérivées partielles d'ordre supérieur :

on traite ici le cas d'une solution réelle à une EDP. Les cas où la dimension de la solution serait plus grande se traitent de façon similaire mais nécessitent des écritures plus complètes ; les cas les plus couramment rencontrés sont la dimension 1 (comme ici), 2 ou 3 (pour des problèmes de mécanique), 6 ou 12 (pour des problèmes d'électromagnétisme respectivement réels ou complexes) ;
les degrés de différentiation supérieurs sont ramenés à un degré moindre par la méthode classique de réduction de degré : on fait intervenir des variables supplémentaires, c'est-à-dire des dérivées partielles des variables de départ (exemple classique : les EDP de la mécanique statique des poutres font intervenir la dérivation partielle d'ordre 4) ; il est parfois possible, pour des degrés supérieurs, d'appliquer plusieurs fois les méthodes de formulation variationnelles afin d'obtenir des ordres plus faibles — en tout cas lorsque le degré de dérivation est pair.

Bien que théoriquement la méthode soit transposable en dimensions supérieures du support, techniquement la complexité de création des discrétisations croît avec la dimension… et pratiquement, on résout rarement des problèmes en dimensions supérieures à 3 — y compris des problèmes de dynamique en espace à 3 dimensions qui pourraient être traités en quatre dimensions mais sont traités en réalité avec une méthode mixte éléments finis « en espace » et en différences finies « en temps ».

Cadre algébrique, analytique et topologique

Soit un domaine (ouvert borné et connexe) Ω de $\mathbb{R}^2$ , de bord δΩ, et d'adhérence (compacte) Ω. Pour simplifier les représentations, on suppose le bord polygonal.

Soient les fonctions de Ω dans $\mathbb{R}$ différentiables sur Ω (compact) et deux fois différentiables sur Ω (ouvert). De telles fonctions sont continues et différentiables sur le bord du compact. Soit V(Ω) l'ensemble de ces fonctions (V est un espace vectoriel de dimension infinie et V₀ est le sous-espace vectoriel de fonctions de V nulles sur le bord δΩ).

Soient les applications continues sur Ω et différentiables sur Ω, de carré sommables sur Ω et de gradient de carré sommable sur Ω (ou de dérivées partielles de carré sommable, ce qui revient au même avec le support de dimension finie). Nommons cet espace $\mathcal{H}_1(\Omega)$ . Cet espace est un espace de Sobolev. On dote cet espace vectoriel d'un produit scalaire issu de celui de L² tel que si (u, v ) appartiennent à cet espace alors le produit scalaire de u et v est :

$\langle u | v \rangle_{ \mathcal{H}_1(\Omega) } = \int_\Omega{ ( \nabla u \cdot \nabla v + u v ) \,\mathrm{d}\omega }$

On note $\mathcal{H}_1^0(\Omega)$ le sous-espace vectoriel de $\mathcal{H}_1(\Omega)$ dont les fonctions sont nulles sur le bord δΩ. L'opérateur $(x,y) \mapsto x \cdot y$ est un produit scalaire sur l'espace $\mathbb{R}^2$

Cas organique

Hypothèses

On considère ƒ une fonction continue sur Ω de carré sommable et u la solution de l'équation aux dérivées partielles suivante sur Ω ( $\displaystyle \Delta$ est l'opérateur laplacien) :

$\displaystyle - \Delta u + k^2 u = f$

Avec la condition au bord u = 0 sur δΩ. Ceci peut également se réécrire u ∈ V₀. Cette condition au bord s'appelle la condition de Dirichlet.

On démontre qu'il existe une solution unique à ce problème d'EDP à l'aide du théorème de Lax-Milgram.

Formulation faible

Soit v ∈ V₀ quelconque. Multiplions les deux parties de l'équation précédente par v puis sommons sur le domaine Ω, puisque v et ƒ sont tous deux de carré sommable sur ce domaine. On obtient l'équation :

$- \int_\Omega{ v \Delta u \,\mathrm{d}\omega } + k^2 \int_\Omega{ v u \,\mathrm{d}\omega } = \int_\Omega{v f \,\mathrm{d}\omega }\,$

On utilise pour le premier terme une intégration par parties^[1] :

$- \int_\Omega{ v \Delta u \,\mathrm{d}\omega } = - \int_{\partial \Omega }{ \frac{ \partial u }{ \partial n } v \,\mathrm{d}s } + \int_\Omega{ ( \nabla u \cdot \nabla v ) \,\mathrm{d}\omega }$

Dans cette formulation, v est nulle sur le bord (v ∈ V₀) ce qui permet d'obtenir la formulation faible du problème :

$\int_\Omega{ \nabla u \cdot \nabla v \,\mathrm{d}\omega } + k^2 \int_\Omega{ v u \,\mathrm{d}\omega } = \int_\Omega{ v f \,\mathrm{d}\omega }$

Si u est deux fois différentiable, il y a équivalence entre cette formulation et celle du problème initial donné dans la section hypothèse et alors la solution de la formulation faible est la même que la solution initiale. On peut donc résoudre la formulation faible au lieu de résoudre le problème initial.

La question de savoir s'il y a équivalence entre la formulation faible et la formulation initiale donnée dans les hypothèses peut être particulièrement délicate dans les cas limites où l'ouvert Ω n'est pas suffisamment régulier (par exemple s'il y a des points singuliers) ou si ƒ n'est pas suffisamment dérivable (si l'on ne suppose pas que ƒ est au moins $L 2$ ). Il faut alors souvent se ramener à une étude au cas par cas et rien ne dit que la formulation faible aura les mêmes solutions que l'équation de départ. Dans la majorité des problèmes physiques la solution est souvent $\mathcal{C}^\infty$ et l'on ne se pose pas de tels problèmes. Néanmoins, pour des domaines avec des points singuliers cette équivalence peut poser problème. Ceci peut être gênant pour l'étude de fissures en mécanique des milieux continus par exemple.

Notations et cadre général

Pour plus de généralité et pour rendre la suite plus lisible on utilisera les notations suivantes :

$a(u,v) = \int_\Omega{ \left(\nabla u \cdot \nabla v + k^2 u v \right) \,\mathrm{d}\omega }$ avec a un opérateur bilinéaire symétrique (de V² dans $\mathbb{R}$ ) ;

$\mathcal{L}(v) = \int_\Omega{ f v \,\mathrm{d}\omega }$ avec $\mathcal{L}$ un opérateur linéaire (de V dans $\mathbb{R}$ ).

On peut résoudre par la méthode des éléments finis toute équation aux dérivées partielles dont la forme faible se met sous la forme

$a( u, v ) = \mathcal{L}(v)$

On montre que a est un opérateur bilinéaire coercif continu selon la norme $\mathcal{H}_1^0$ (cf. espace de Sobolev) et $\mathcal{L}$ un opérateur linéaire continu également selon la norme $\mathcal{H}_1^0$ . Avec ces notations, le problème se reformule ainsi :

$\forall v \in V_0, a( u, v ) = \mathcal{L}(v)$

Puisque k>0, le théorème de Lax-Milgram assure l'existence de la solution et montre que u, solution du problème précédent, est la solution unique du problème d'optimisation de la fonctionnelle suivante :

$\forall v \in V_0, \mathcal{J}(v) = \frac{1}{2} a( v, v ) - \mathcal{L}(v)$

Cette égalité peut avoir un sens physique notamment du point de vue de l'énergie pour certaines équations physiques et peut servir à montrer l'existence et l'unicité de la solution grâce aux propriétés de a et de $\mathcal{L}$ (linéarité, coercivité, …).

Choix d'un maillage et discrétisation

Choix d'un maillage

Un exemple de maillage triangulaire

La méthode des éléments finis repose sur un découpage de l'espace selon un maillage. D'habitude l'on choisit un maillage carré ou triangulaire mais rien n'interdit de choisir des maillages plus complexes. Il n'est pas non plus nécessaire que le maillage soit régulier et l'on a tendance à resserrer le maillage près des endroits d'intérêt (par exemple aux endroits où l'on pense que la solution va beaucoup varier) ; cependant, il faut veiller à avoir des éléments faiblement distordus (se rapprocher d'un polygone régulier). Plus ce maillage est resserré, plus la solution que l'on obtient par la méthode des éléments finis sera précise et proche de la « vraie » solution de l'équation aux dérivés partielles.

Fonctions de base

Fonction de base en dimension 1. Les x_i sont les nœuds du réseau.

On doit après prendre une base de fonctions « adaptées » au maillage. Plusieurs choix sont alors possibles. En général, les fonctions de base utilisées pour les éléments finis sont interpolantes, c'est-à-dire que les valeurs nodales sont les valeurs des grandeurs inconnues aux nœuds.

La plus simple est l'emploi des polynômes de Lagrange. Dans cette méthode les fonctions de base valent 1 à un nœud du maillage et 0 à tous les autres. La fonction de base i est alors la fonction valant 1 au nœud i et 0 sur les autres nœuds et qui est polynomiale sur chaque élément. Un exemple de telles fonctions est représenté en dimension 1 à côté. Il y a autant de fonctions de base par élément que de nombre de nœuds.

On appelle élément la donnée d'une géométrie (souvent polygonale en 2D, polyédrique en 3D) et de fonctions de base associées à cette géométrie.

D'autres solutions peuvent exister pour les fonctions de base. On cite ici un seul exemple les éléments finis d'Hermite qui ont la particularité d'avoir deux fonctions de base associées à chaque nœud. Dans cette version, la valeur de la solution est ajustée avec la première fonction alors que la deuxième permet d'ajuster la valeur de la dérivée. Ce type de fonctions de base peut avoir un intérêt pour la résolution de certaines équations aux dérivées partielles (par exemple l'équation des plaques en mécanique des milieux continus), même si elle nécessite d'avoir deux fois plus de fonctions pour un maillage donné.

Quelques éléments classiques

En 2D

triangles de degré 1, (triangles à 3 nœuds, fonctions linéaires)
triangles de degré 2 (triangles à 6 nœuds, polynômes de degré 2)
quadrangles de degré 1 (carrés à quatre nœuds, fonctions linéaires)
quadrangles de degré 2 (carrés à 8 ou 9 nœuds, polynômes de degré 2)

En 3D

tétraèdre de degré 1, (quatre nœuds, linéaires)
cube de degré 1, (huit nœuds, linéaire)

Les deux fonctions de base d'Hermite associées au nœud 0 avec les nœuds voisins en +1 et -1 en dimension 1

Discrétisation

Soit le maillage $\mathcal{M}$ et la base $b = (e 1 ... e n)$ associée. Puisque la condition de Dirichlet impose des fonctions nulles aux bords, on utilise uniquement la sous-base $b$ limitée aux points intérieurs de $Ω$ .

On cherche la solution $\bar{u}$ du problème discrétisé ainsi :

$\bar{u} \in V_n^0 | \forall v \in V_n^0, a( \bar{u}, v ) = \mathcal{L}(v)$

Or dans cet espace discrétisé, dire que tout vecteur vérifie la proposition précédente est équivalent à dire que tous les vecteurs de la base vérifient la proposition. Si l'on décompose la solution $\bar{u}$ dans la base des $e i$ intérieurs, en composantes $u i$ , on obtient :

$\forall j \in [1,...,n] \sum_{i =1}^n { u_i a( e_i, e_j ) } = \mathcal{L}(e_j)$

L'idée est que quand le maillage se resserre et que le nombre de fonctions de base n tend vers l'infini (et que l'espace engendré par cette base $V_n^0$ croit vers V₀), les solutions u_n devront converger vers la solution u de l'équation aux dérivées partielles de départ.

Éventuelle deuxième discrétisation

Dans certains problèmes physiques, il peut être intéressant de discrétiser une deuxième fois. Cette seconde discrétisation n'est pas nécessaire pour la méthode des éléments finis. Souvent on a comme expression de $\mathcal{L}$ :

$\mathcal{L}(e_j)=\int_\Omega f\cdot e_j$

On projette alors f sur la base b. On obtient:

$f_n = \sum_{k=1}^n f_k e_k.$

et on approche $\mathcal{L}(e_j)= \int_\Omega f\cdot e_j$ par $\sum_{k=1}^n f_k \int_\Omega e_k e_j,\; j=1,\dots,n.$

Le problème est d'obtenir ensuite une projection $f n$ acceptable sachant qu'il n'y a pas nécessairement de produit scalaire associé à la base qui permette de projeter de façon efficace. Dans les deux exemples de bases donnés plus haut, cette projection est aisée. Dans le cas des éléments finis de Lagrange, la projection sur la fonction e_i est donnée par la valeur en x_i ; dans le cas des éléments d'Hermite, c'est la valeur de la fonction ainsi que de sa dérivée qui permettent d'obtenir la projection. Pour d'autres bases, la projection peut être plus compliquée.

Problème sous forme matricielle

Si l'on note:

la matrice $A$ ayant pour composantes les $a (e i, e j)$ ,
le vecteur $U$ ayant pour composantes les $u i$ qui sont les coordonnées de la solution approché sur la base b
le vecteur $B$ ayant pour composantes les $\mathcal{L}( e_j )$

alors ce problème revient à résoudre l'équation linéaire de $n$ équations à $n$ inconnues :

$\mathbf{A} U = B$

La matrice A est appelée matrice de rigidité par analogie avec certains problèmes de mécanique des solides. $A$ est par construction symétrique, et puisque $a$ est coercive, alors $A$ est symétrique, définie positive donc inversible. On obtient donc l'existence et l'unicité de $U = A - 1 B$ . grâce aux coordonnées de $\bar{u}$ sur la base b on peut alors construire la solution approchée $\bar{u}$ . Quand le maillage se resserre cette solution approchée va tendre vers la vraie solution de l'équation aux dérivées partielles de départ.

Pour le cas avec une deuxième discrétisation de $\mathcal{L}( e_j )$ on obtient:

$\mathbf{A}U=\mathrm{M}f$

où M est appelée la matrice de masse et contient les $\int_\Omega e_i \cdot e_j$ . f est un vecteur contenant les coordonnées de f dans la base. La méthode est alors la même qu'avec une seule discrétisation puisque A vérifie les mêmes propriétés. Cette méthode peut parfois être préférée quand on peut obtenir de façon simple la projection de f sur la base et la matrice M.

Algorithme

La méthode des éléments finis doit être conduite ainsi

On calcule la matrice de rigidité A
On détermine le membre de droite, en calculant les termes $\mathcal{L}(e_j)$ ou alors par l'intermédiaire de la matrice de masse.
On résout le problème AU=B ou le problème AU=Mf suivant le niveau de discrétisation choisi. U est alors donné par $U = A - 1 B$ . Selon la base qui a été choisie et selon les données du problème, il faut choisir la méthode d'inversion la plus efficace pour A. C'est l'étape la plus consommatrice en termes de puissance de calcul, et l'efficacité de la méthode en termes de temps de calcul se joue principalement sur cette étape.
On peut écrire $\bar{u}$ grâce au vecteur U qui contient les coordonnées de $\bar{u}$ sur la base b et obtenir une solution approchée au problème.

Condition de Neumann

La condition qui suit est très différente de celle de Dirichlet. On pose comme condition au bord que la dérivée normale existe sur le bord $\bar{\Omega}$ , et que la condition de Neumann $\frac{\partial u}{\partial n}(\overline{\Omega}) = 0$ est vérifiée.

Si la fonction est supposée différentiable au bord $D_u(X) \cdot n = 0, \forall X \in \overline{\Omega}$ , voire si elle admet un gradient $\langle \nabla u(X) | n \rangle = 0, \forall X \in \overline{\Omega}$ .

Le résultat fonctionne de la même manière car l'élément clef de la démonstration où intervient l'hypothèse de bord est que l'intégrale $\int_\Omega{\frac{\partial u}{\partial n} v \,\mathrm{d}\omega}=0$ parce que cette fois-ci ce n'est pas la fonction test mais la dérivée normale qui est nulle.

Par la suite, la différence réside surtout dans le choix des vecteurs de base pour la discrétisation : il faut conserver les fonctions tests propres aux nœuds du bord.

Exemples issus de problèmes physiques

Historique

Analyse des structures née vers 1850
- Résistance des matériaux ⇒ calculs « manuels »
  Maxwell, Castigliano, Mohr
- Concept d'éléments finis né vers 1940
  Newmark, Hrenikoff, Mc Henry, Courant
- Développement réel depuis 1960
  Calcul numérique sur ordinateur

Domaines d'application

Calcul de structures, étude des contacts, électricité, électromagnétisme, hydraulique, aérodynamique, finance, ingénierie biomédicale, ...

Principe

Le milieu continu est « idéalisé » par la subdivision en un nombre fini d'éléments dont le comportement est représenté par un nombre finis de paramètres.
La résolution du problème global, obtenu par assemblage des éléments, suit les règles qui régissent les structures discrètes.

Les difficultés

D'ordre théorique : formulation des éléments
D'ordre pratique :
- Discrétisation du milieu continu (maillage)
- Qualité des résultats (convergence de la méthode)

Exemple de problème discret : un réseau électrique

Problème discret

Équation locale du composant e :

$\left. \begin{matrix} I_i^e = {1 \over R^e} (U_i^e - U_j^e) \\ I_j^e = {1 \over R^e} (U_j^e - U_i^e) \end{matrix} \right\} \Longrightarrow \begin{Bmatrix} I_i^e \\ I_j^e \end{Bmatrix} = {1 \over R^e} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}\begin{Bmatrix} U_i^e \\ U_j^e \end{Bmatrix} \,$

soit $\left\{ I^e \right\} = \left[ K^e \right] \left\{ U^e \right\} \,$
On écrit :
- La continuité des potentiels en chaque connexion $i \,$
- L'équilibre des courants à chaque connexion
- L'adjonction des courants externes $P^i \,$
On obtient l'équation globale du système assemblé :

$P^i = \sum_{j=1}^m \sum_{e=1}^m K_{ij}^e U_j^e \,$

soit $\left\{ P \right\} = \left[ K \right] \left\{ U \right\} \,$

Définition d'un élément fini

Milieu continu

Milieu discrétisé

En calcul de structures, un élément fini est caractérisé par deux matrices :

La matrice de raideur $\left[ K \right] \,$
La matrice de masse $\left[ M \right] \,$

Formulation d'un élément fini

Définitions et notations

Déplacement : $\left\{ U \right\} \,$
C'est un vecteur dont chaque composante est également appelée degré de liberté (ddl)
- 3 ddl de translation : $U_x,U_y,U_z \,$
- 3 ddl de rotation : $\theta_x,\theta_y,\theta_z \,$

Déformation : (voir Tenseur des déformations) $\left[ \epsilon \right] \,$

C'est le rapport de l'allongement à la longueur initiale.

En petites déformations, on a $(A'B')^2 = \left(\ dx + {\partial u \over \partial x} \ dx\right)^2 + \left({\partial v \over \partial x} \ dx\right)^2 \,$

$\epsilon_x = {{A'B'-AB} \over AB} \,$

Comme $AB=\ dx \,$ , on a $A'B'=(1+\epsilon_x)\ dx \,$

$\Rightarrow 2\epsilon_x+\epsilon_x^2 = 2{\partial u \over \partial x}+\left({\partial u \over \partial x}\right)^2+\left({\partial v \over \partial x}\right)^2 \,$

On néglige les termes d'ordre 2 :

$\epsilon_x = {\partial u \over \partial x} \,$

Remarque : $\epsilon \,$ est sans dimension

Contrainte : (voir Tenseur des contraintes)
- Elle représente les efforts internes qui s'appliquent dans la structure.
$\sigma_{11},\sigma_{22},\sigma_{33} \,$ : contraintes normales

$\sigma_{12},\sigma_{13},\sigma_{23} \,$ : contraintes de cisaillement
- Une contrainte est homogène à une pression (N/m²)
- Il existe un système de coordonnées dans lequel $\left[ \sigma \right] \,$ est une matrice diagonale : $\left[ \sigma \right] = \begin{bmatrix}\sigma_X & 0 & 0 \\ 0 & \sigma_Y & 0 \\ 0 & 0 & \sigma_Z\end{bmatrix} \,$
$\sigma_X,\sigma_Y,\sigma_Z \,$ sont appelées les contraintes principales

Relations contraintes-déformations : (voir Loi de Hooke) ≡ lois de comportement

$\begin{Bmatrix}\sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \sigma_{12} \\ \sigma_{23} \\ \sigma_{31}\end{Bmatrix} = {{E(1-\nu)} \over {(1+\nu)(1-2\nu)}} \begin{bmatrix}1 & {\nu \over {1-\nu}} & {\nu \over {1-\nu}} & 0 & 0 & 0 \\ & 1 & {\nu \over {1-\nu}} & 0 & 0 & 0 \\ & & 1 & 0 & 0 & 0 \\ & & & {(1-2\nu) \over {2(1-\nu)}} & 0 & 0 \\ & \mbox{(sym)} & & & {(1-2\nu) \over {2(1-\nu)}} & 0 \\ & & & & & {(1-2\nu) \over {2(1-\nu)}}\end{bmatrix} \begin{Bmatrix}\epsilon_{11} \\ \epsilon_{22} \\ \epsilon_{33} \\ \gamma_{12} \\ \gamma_{23} \\ \gamma_{31}\end{Bmatrix}\,$

$E \,$ : module de Young (N/m²)

$\nu \,$ : coefficient de Poisson (sans dimension)

On utilise parfois le module de cisaillement : $G = {E \over {2(1+\nu)}} \,$
Pour un matériau isotrope, il n'y a que 2 paramètres indépendants. Il y en a 6 pour un matériau isotrope transverse, 9 pour un matériau orthotrope et 21 pour un matériau anisotrope
En notation matricielle, on écrit : $\left\{ \sigma \right\} = \left[D\right]\left\{ \epsilon \right\} \,$

$\left[D\right] \,$ est appelée matrice d'élasticité du matériau.

Énergie de déformation : $W \,$

$W = {1 \over 2}\int_{v}\sigma.\epsilon.\,\mathrm{d}v \,$

Travail d'une force

C'est le produit de la force par le déplacement de son point d'application : $\tau_F = {1 \over 2}F.U_F \,$

Moment

C'est une force appliquée sur un ddl de type rotation

Équations fondamentales

Équations d'équilibre local: ${\partial \sigma_x \over \partial x} + {\partial \sigma_{xy} \over \partial y} + {\partial \sigma_{xz} \over \partial z} + F_x = 0\,$; ${\partial \sigma_y \over \partial y} + {\partial \sigma_{xy} \over \partial x} + {\partial \sigma_{yz} \over \partial z} + F_y = 0\,$; ${\partial \sigma_z \over \partial z} + {\partial \sigma_{zx} \over \partial x} + {\partial \sigma_{zy} \over \partial y} + F_z = 0\,$

Relations déformations-déplacements

${\epsilon_x= {\partial u \over \partial x}} \qquad {\epsilon_y= {\partial v \over \partial y}} \qquad {\epsilon_z= {\partial w \over \partial z}} \,$

$\gamma_{xz}={\partial w \over \partial x} + {\partial u \over \partial z} \,$

$\gamma_{xy}={\partial u \over \partial y} + {\partial v \over \partial x} \,$

$\gamma_{yz}={\partial w \over \partial y} + {\partial v \over \partial z} \,$

Symboliquement, on écrit $\{\epsilon\} = [S]\{U\} \,$

Signification du coefficient de Poisson

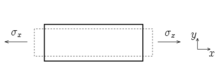
Si on applique au barreau une contrainte $\sigma_x \,$ , on observe un rétrécissement dans la direction y correspondant à une déformation $-\nu \sigma_x \over E \,$

Quelques valeurs usuelles :

Acier : E = 2,1E11 N/m² = 210 000 MPa $\nu \,$ = 0,3
Aluminium : E = 7E10 N/m² = 70 000 MPa $\nu \,$ = 0,3

Remarques : On a toujours -1 $\le \nu \le \,$ 0,5
Quand $\nu \to \,$ 0.5, le matériau est dit incompressible.

Exemple de formulation : Barre en traction

On suppose que le déplacement en tout point de la barre est donné par un polynôme du 1^er degré : $u(x) = a_1 + a_2 x \,$

On a $u(0) = u_1 \,$ et $u(L) = u_2 \,$

d'où $u(x) = u_1\left(1-{x \over L} \right) + {x \over L} u_2 \,$

qu'on écrit symboliquement : $u(x) = [N(x)]\{U\} \,$ avec $\left|\begin{matrix}[N(x)] & = & \left[ \left(1-{x \over L}\right) ; \left({x \over L}\right) \right] \\ \{U\} & = & \begin{Bmatrix}u_1 \\ u_2 \end{Bmatrix} \end{matrix}\right. \,$
On en déduit :

$\epsilon = \left[-{1 \over L} ; {1 \over L} \right]\begin{Bmatrix}u_1 \\ u_2\end{Bmatrix} = [B]\{U\} \,$

$\sigma = E\left[-{1 \over L} ; {1 \over L} \right]\begin{Bmatrix}u_1 \\ u_2\end{Bmatrix} = [D]\epsilon \,$

D'autre part, on a par définition :

$\begin{Bmatrix}F_1 \\ F_2 \end{Bmatrix} = \begin{Bmatrix}-\sigma S \\ \sigma S \end{Bmatrix} \,$ où S est l'aire de la section de la barre.

On pose :

$\{F\} = \begin{Bmatrix}F_1 \\ F_2 \end{Bmatrix} = [A]\sigma \qquad \mbox {avec} \qquad \{A\} = S \begin{Bmatrix}-1 \\ 1 \end{Bmatrix} \,$

On obtient finalement :

$\{F\} = [A][D][B]\{U\} \,$

Soit une relation du type :

$\{F\} = [K]\{U\} \qquad \mbox {avec} \qquad [K] = [A][D][B] \,$

En explicitant :

$[K] = {ES \over L} \begin{bmatrix}1 & -1 \\ -1 & 1 \end{bmatrix} \,$

On voit que la matrice de rigidité se calcule comme le produit de 3 matrices :

$[B] \,$ : Transformation des déplacements aux déformations

$[D] \,$ : Matrice d'élasticité du matériau

$[A] \,$ : Transformation des contraintes en forces

Formulation générale (méthode directe)

La démarche est la suivante :

On exprime le déplacement $\{u(x)\}\,$ en tout point de l'élément en fonction des déplacements aux nœuds $\{u(x)\} = [N(x)]\{U\}\,$
On exprime les déformations en fonction des déplacements $\{\epsilon(x)\}=[S]\{u(x)\}\,$

d'où $\{\epsilon(x)\}=[S]\{N(x)\}\{U\}=[B(x)]\{U\}\,$

On écrit la loi de comportement du matériau qui relie les contraintes aux déformations : $\{\sigma(x)\}=[D]\{\epsilon(x)\}\,$
On écrit que le travail des forces externes appliquées à la structure pour un déplacement virtuel $\delta U \,$ est égal au travail interne des contraintes pour ce même déplacement :

$\{\delta U\}^T\{F\}=\int_V \{\delta \epsilon\}^T\{\sigma\} \,\mathrm{d}v \,$

En explicitant, on a :

$\{\delta U\}^T\{F\}=\{\delta U\}^T \left (\int_V [B]^T[D][B] \,\mathrm{d}v \right ) \{U\} \,$

Comme cette relation est vraie pour tout déplacement virtuel, on en déduit :

$\{F\}=[K]\{U\} \,$

avec $[K] \,$ sous sa forme plus générale : $[K]=\int_V [B]^T[D][B] \,\mathrm{d}v \,$

Remarques

La relation ci-dessus montre que $[K] \,$ est symétrique.
Le terme courant $K_{ij} \,$ de la matrice correspond à la force qui s'exerce sur le nœud $j \,$ lorsqu'on impose un déplacement unitaire du nœud $i \,$ .

La symétrie de $[K] \,$ qui s'écrit $K_{ij} = K_{ji} \,$ correspond mécaniquement au théorème de réciprocité de Maxwell-Betti.

Qu'est-ce qui va différencier les différents types d'éléments finis ?

Le choix des fonctions N(x)
La nature de l'opérateur S (reliant déformations et déplacements) qui dépend du type de théorie élastique utilisée :
- théorie des poutres
- théorie des plaques
- théorie de la contrainte ou de la déformation plane
- théorie des coques
- théorie des corps de révolution
- théorie de l'élasticité 3D

Remarques

Nous avons décrit le processus de formulation d'un élément fini dans le cadre de la méthode directe (dite aussi méthode des déplacements). Il existe d'autres approches :

La méthode des résidus pondérés
L'application du principe des travaux virtuels ou des puissances virtuelles
La minimisation de l'énergie potentielle

Toutes ces approches sont équivalentes et aboutissent à la construction de la même matrice de rigidité.

Éléments finis en contrainte

Au lieu de rechercher une solution approchée en déplacement, on peut aussi rechercher la solution approchée en contrainte.

Dans le cas de la mécanique, l'application du principe des puissances virtuelles donne de manière non triviale les théorèmes énergétiques. On peut aboutir au même résultat en quelques lignes en écrivant l'erreur en relation de comportement.

L'approche en contrainte consiste à rechercher dans l'espace des champs de contraintes admissibles celui qui réalise le minimum de l'énergie complémentaire.

Cette approche est plus précise que l'approche en déplacement mais elle est peu développée du fait de la difficulté que l'on a à générer des champs de contraintes de divergence donnée.

Étude des fonctions N(x)

Dans le cas général de l'élasticité tridimensionnelle, ce sont en fait des fonctions de x, y, z.
Les fonctions les plus couramment utilisées sont des polynômes.
- Polynôme de degré 1 : élément linéaire (2 nœuds par arête)
- Polynôme de degré 2 : élément parabolique (3 nœuds par arête)
- Polynôme de degré 3 : élément cubique (4 nœuds par arête)

Les fonctions N(x) sont appelées fonctions de forme ou fonctions d'interpolation de l'élément.

Les éléments isoparamétriques

$[K]=\int_V [B]^T[D][B] \,\mathrm{d}v \,$

Problème

Soit on construit $[K] \,$ pour un certain nombre d'éléments de forme et de géométrie figée ⇒ nécessité, pour mailler une structure complexe, d'utiliser un grand nombre d'éléments.
Soit on utilise des éléments à géométries variables ⇒ il faut reconstruire $[K] \,$ à chaque fois.

D'où l'idée

Pour construire la matrice de raideur d'un élément à géométrie variable, on va utiliser des fonctions d'interpolation pour décrire non seulement le champ de déplacement de l'élément mais également sa géométrie. De plus, on va travailler en coordonnées locales.

Interpolation de la géométrie

$\begin{matrix}x &=&\ &\tilde N_1(x)x_1 + \tilde N_2(x)x_2 \\ \ &\ &+&\tilde N_3(x)x_3 + \tilde N_4(x)x_4\end{matrix} \,$

Idem pour les autres coordonnées.

Coordonnées locales (cas 2D)

Élément isoparamétrique

Un élément est dit isoparamétrique si on prend les mêmes fonctions d'interpolation pour le déplacement et la géométrie.
$\tilde N(x) = N(x) \,$

Autres classes d'éléments

Évaluation de K

La forme générale s'écrit :
$[K]=\int_x \int_y \int_z G(x,y,z) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \,$
On passe en variables locales $\xi,\eta,\zeta \,$
On a $\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = \det (J)\,\mathrm{d}\xi \,\mathrm{d}\eta \,\mathrm{d}\zeta \,$

$J \,$ s'appelle la matrice jacobienne.

On est alors amené à calculer des intégrales du type :
$\int_{-1}^{+1} \int_{-1}^{+1} \int_{-1}^{+1} G(\xi ,\eta ,\zeta) \det J\ \,\mathrm{d}\xi \,\mathrm{d}\eta \,\mathrm{d}\zeta \,$

Bénéfice de l'approche

On s'est ramené à un domaine d'intégration simple et invariant pour lequel on peut appliquer les formules de quadrature de gauss :
$\int_{-1}^{+1} f(x) \,\mathrm{d}x = \sum_{k=1}^n H_k f(a_k) \,$ les $a_k \,$ et $H_k \,$ étant tabulés.
Les $a_k \,$ sont appelés points d'intégration de l'élément ou encore points de Gauss de l'élément.

Cas particulier : les éléments axisymétriques

Décomposition en série de Fourier :

$u(r,\theta,z) = \sum_n u_n^s(r,z)\cos (n\theta) + \sum_n u_n^s(r,z)\sin (n\theta) \,$

L'axisymétrie correspond à la restriction $n=0 \,$ de cette décomposition.

$u(r,\theta,z) = u_n^s (r,z) \,$

Remarque

Pour utiliser ce type d'élément, le problème doit être globalement axisymétrique :

la géométrie
les conditions limites
le chargement

Processus de calcul (cas statique)

Maillage
Construction de la matrice de raideur de chaque élément $[K^e] \,$
Assemblage de la matrice globale $[K] \,$
Construction du vecteur chargement $\{F\} \,$
Élimination de certains ddl (si besoin)
Résolution : $\{U\} = [K^{-1}]\{F\} \,$
Calcul des quantités dérivées de $\{U\} \,$

$\{\epsilon^e\} = [B^e] \{U^e\} \,$

$\{\sigma^e\} = [D^e] \{\epsilon^e\} \,$

$W^e = {1 \over 2} \{\epsilon^e\}^T \{\sigma^e\} \,$

Logiciels d'éléments finis

Quelques exemples de logiciels utilisant la méthode des éléments finis en mécanique des structures :

ABAQUS : logiciel pluridisciplinaire développé par la société Simulia (Dassault Systèmes)
ANSYS : logiciel pluridisciplinaire développé par Ansys
CAST3M : logiciel pluridisciplinaire français développé par le CEA (gratuit pour l'enseignement et la recherche)
ASTER : logiciel pluridisciplinaire libre français développé par EDF
COMSOL MULTIPHYSICS : logiciel élément finis alliant généricité (mécaniques des fluides, électromagnétisme, mécaniques des structures, thermique) et puissance de calcul, permettant notamment d'étudier un nombre illimité d'interactions entre différentes physiques (fluide caloporteur par exemple),
CosmosWorks : Logiciel Franco-Américain appartenant à SolidWorks qui lui-même appartient à Dassault
Dytran : logiciel américain développé par MSC.Software
EuroPlexus : logiciel français
Flux2D/3D : logiciel 2D&3D éléments finis français (développé en collaboration avec le GE2Lab) permettant le calcul des états magnétiques, électriques ou thermiques en régimes permanents, harmoniques et transitoires, avec des fonctionnalités d'analyse multi-paramétrique étendue, les couplages circuit et cinématique.
FreeFem++ : logiciel pluridisciplinaire libre.
ICAB : logiciel de calcul pour poutres et coques avec vérifications réglementaires selon Document technique unifié DTU France (NV65, CM66, AL76, CB71...), Eurocodes, AISC américain
IMPETUS Afea Solver : logiciel de calcul de grandes déformations utilisant des éléments finis isogéométriques d'ordre 3.
JMAG : logiciel Japonais (distribué en Europe par Powersys) permet un couplage entre les analyses électromagnétiques et structurelles.
LS-DYNA : logiciel de dynamique rapide américain
Marc : logiciel de grandes déformations américain développé par MSC.Software
Morfeo : logiciel belge
MSC.Nastran : logiciel Pluridisciplinaire américain développé par MSC.Software
NX.Nastran : logiciel développé par Siemens
PAM-CRASH : logiciel de dynamique rapide (crash) développé par la société française ESI
PAM-STAMP : logiciel de simulation d'emboutissage et de mise en forme de tôle, développé par la société française ESI
PERMAS : logiciel pluridisciplinaire développé par la société allemande INTES GmbH, basée à Stuttgart.
Radioss : logiciel pluridisciplinaire développé par la société américaine Altair
ROBOT MILLENIUM : logiciel français développé par ROBOBAT pour le calcul de structures de type génie civil et bâtiment, il est intégré ensuite par AutoDesk
SAMCEF : logiciel pluridisciplinaire belge
Structurix : Programme gratuit de calcul de résistance des matériaux. Il permet de résoudre des problèmes 2D et 3D avec des éléments : barres et poutres. Des problèmes 2D avec des éléments triangulaires. Des problèmes de flexion des plaques à l'aide d'éléments rectangulaires.
ZeBuLoN : logiciel pluridisciplinaire développé par MINES ParisTech, l'ONERA et NorthWest Numerics, specialisé dans les comportements non linéaires des matériaux
SYSWELD : logiciel de Thermo-méco-métallurgie français basé sur SYSTUS développé par la société ESI

Notes et références

↑ Pour certains cas limites lorsqu'il n'y a pas suffisamment de régularité et que l'intégration par parties n'a pas de sens on utilise aussi une formulation adaptée du théorème de Stokes mais il faut alors définir la dérivée faible puis la divergence faible, ce qui entraine des complications supplémentaires.

Voir aussi

Sur les autres projets Wikimedia :

« Méthode des éléments finis », sur Wikibooks (livres pédagogiques)

Bibliographie

G. Allaire and A. Craig: Numerical Analysis and Optimization:An Introduction to Mathematical Modelling and Numerical Simulation
O. C. Zienkiewicz, R. L. Taylor, J.Z. Zhu : The Finite Element Method: Its Basis and Fundamentals Butterworth-Heinemann; 6 edition (March 21, 2005) (ISBN 0750663200)
J. Chaskalovic, "Méthode des éléments finis pour les sciences de l'ingénieur", (2004), Ed. Lavoisier. (ISBN 2-7430-0708-7)
K. J. Bathe : Numerical methods in finite element analysis Prentice-Hall (1976) (ISBN 0136271901)
Chu-Kia Wang : Matrix methods of structural analysis International Textbook Co; 2d ed edition (1970) (ISBN 0700222677)
R. H Gallagher : Introduction aux éléments finis Pluralis (1977)
N. Willems : Matrix analysis for structural engineers Prentice-Hall (1968) (ISBN 0135654998)

Liens externes

(fr) Liens vers des codes éléments finis téléchargeables
(fr) RDM Le Mans v.6, logiciel téléchargeable
(en) La méthode des éléments finis en génie biomedicale et en biomécanique
(fr) La méthode des éléments finis
(fr) Méthodes numériques appliquées à la conception par éléments finis
(fr) Formulations mathématiques et résolution numérique en mécanique

Catégories :

Mécanique des milieux continus
Équations différentielles numériques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode des éléments finis de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Methode des elements finis — Méthode des éléments finis Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode Des Éléments Finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Methode des elements finis etendus — Méthode des éléments finis étendus La Méthode des éléments finis (MEF) est un outil bien maîtrisé actuellement, tant d un point de vue recherche et développement que d un point de vue utilisation dans l industrie. C est une méthode robuste qui a… … Wikipédia en Français
Méthode des Eléments Finis Etendus — Méthode des éléments finis étendus La Méthode des éléments finis (MEF) est un outil bien maîtrisé actuellement, tant d un point de vue recherche et développement que d un point de vue utilisation dans l industrie. C est une méthode robuste qui a… … Wikipédia en Français
Méthode des éléments finis étendus — La méthode des éléments finis (MEF) est un outil bien maîtrisé actuellement, tant d un point de vue recherche et développement que d un point de vue utilisation dans l industrie. C est une méthode robuste qui a fait ses preuves, mais les défis d… … Wikipédia en Français
Méthode des éléments finis de frontière — La méthode des éléments finis de frontière, méthode des éléments frontière ou BEM Boundary Element Method en anglais, est une méthode de résolution numérique. Elle se présente comme une alternative à la méthode des éléments finis avec la… … Wikipédia en Français
Methode des volumes finis — Méthode des volumes finis En analyse numérique, la méthode des volumes finis est utilisée pour résoudre numériquement des équations aux dérivées partielles, comme la méthode des différences finies et la méthode des éléments finis. Mais,… … Wikipédia en Français
Méthode Des Volumes Finis — En analyse numérique, la méthode des volumes finis est utilisée pour résoudre numériquement des équations aux dérivées partielles, comme la méthode des différences finies et la méthode des éléments finis. Mais, contrairement à la méthode de… … Wikipédia en Français
Méthode des volumes finis — En analyse numérique, la méthode des volumes finis est utilisée pour résoudre numériquement des équations aux dérivées partielles, comme la méthode des différences finies et celle des éléments finis. Contrairement à la méthode des différences… … Wikipédia en Français
Éléments finis — Méthode des éléments finis Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Méthode des éléments finis

Sommaire

Introduction

Méthode des éléments finis

Principe général

Dimensions

Cadre algébrique, analytique et topologique

Cas organique

Hypothèses

Formulation faible

Notations et cadre général

Choix d'un maillage et discrétisation

Choix d'un maillage

Fonctions de base

Quelques éléments classiques

Discrétisation

Éventuelle deuxième discrétisation

Problème sous forme matricielle

Algorithme

Condition de Neumann

Exemples issus de problèmes physiques

Historique

Domaines d'application

Principe

Les difficultés

Exemple de problème discret : un réseau électrique

Définition d'un élément fini

Formulation d'un élément fini

Définitions et notations

Équations fondamentales

Exemple de formulation : Barre en traction

Formulation générale (méthode directe)

Éléments finis en contrainte

Étude des fonctions N(x)

Les éléments isoparamétriques

Problème

D'où l'idée

Interpolation de la géométrie

Coordonnées locales (cas 2D)

Élément isoparamétrique

Autres classes d'éléments

Évaluation de K

Bénéfice de l'approche

Cas particulier : les éléments axisymétriques

Processus de calcul (cas statique)

Logiciels d'éléments finis

Notes et références

Voir aussi

Articles connexes

Bibliographie

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link