Théorie des plaques

Pour les articles homonymes, voir Plaque.

La théorie des plaques est une théorie permettant de calculer les déformations et les contraintes dans une plaque soumise à des charges. Elle s'inspire de la théorie des poutres.

Sommaire

1 Historique
2 Démarche
3 Définitions et hypothèses
4 Théorie des plaques minces
5 Déformation de membrane
6 Théorie des plaques épaisses
7 Notes
8 Voir aussi
- 8.1 Liens externes

Historique

En 1888, Love utilise les hypothèses de Gustav Kirchhoff, elles-mêmes inspirées des hypothèses d'Euler-Bernoulli pour les poutres, pour fonder une théorie des plaques minces^[1].

La théorie des plaques épaisses a été consolidée par Mindlin (en)^[2] à partir des travaux de Rayleigh (1877), Timoshenko (1921), Reissner (1945) et Uflyand (1948)

Démarche

Démarche pour l'étude des plaques

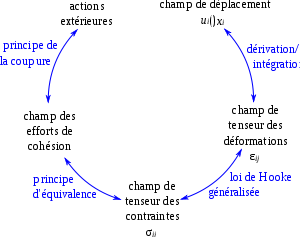
Comme pour l'étude des poutres, on met en relation

la forme finale de la plaque, c'est-à-dire le champ des déplacements, avec le champ de tenseur des déformations ;
les efforts de cohésion avec les efforts extérieurs ;
les efforts de cohésion avec le tenseur des contraintes, grâce au principe d'équivalence ;
et le tenseur des contraintes avec le tenseur des déformations, grâce à la loi de Hooke généralisée.

Le modèle de poutre permet de passer des efforts de cohésion au tenseur des contraintes ; il permet d'appliquer le principe d'équivalence.

Définitions et hypothèses

Une plaque est un solide délimitée par deux plans parallèles, les faces, et un cylindre au sens large (de section quelconque et pas nécessairement circulaire) dont l'axe est perpendiculaire aux faces. On définit :

le plan moyen, ou plan médian : plan situé à équidistance entre les faces (c'est l'équivalent de la courbe moyenne des poutres) ;
le feuillet neutre : élément de matière d'épaisseur infinitésimale situé autour du plan moyen (c'est l'équivalent de la fibre neutre des poutres) ; c'est le plan (O, x, y), d'équation z = 0 ;
une fibre normale : ensemble des points situés sur une normale au plan médian, à un endroit (x, y) donné ; elle a pour direction z.

On appelle h l'épaisseur de la plaque ; le plan inférieur est donc le plan z = -h/2 et le plan supérieur est le plan z = h/2.

On se place dans le cas d'un matériau continu, élastique, homogène et isotrope.

Si, au repos, les faces ne sont pas planes, on parle de coque plutôt que de plaque.

On sépare l'étude en deux parties : pour l'étude de la flexion, on considère que les charges sont perpendiculaires aux faces, donc que les forces sont de la forme

$\vec{\mathrm{F}} = \begin{pmatrix} 0 \\ 0 \\ \mathrm{F} \end{pmatrix}$

et que les couples sont de la forme

$\vec{\mathrm{M}} = \begin{pmatrix} \mathrm{M}_x \\ \mathrm{M}_y \\ 0 \end{pmatrix}$ .

Pour les charges situées dans le plan des faces, on parle de voile ou de membrane.

Théorie des plaques minces

Déformation d'une plaque mince (contour gris) avec mise en évidence du déplacement d'un élément de matière (contour noir), de son feuillet moyen (rouge) et de sa fibre normale (bleue)

La théorie des plaques minces, ou théorie de Love-Kirchhoff, suppose que

le plan moyen (équivalent de la courbe moyenne des poutres) est initialement plan ;
le feuillet moyen (équivalent de la fibre neutre des poutres) ne subit pas de déformation dans son plan ; on ne considère que le déplacement transversal w des points du feuillet moyen ;
modèle de Kirchhoff : les sections normales au feuillet moyen restent normales lors de la déformation ; en conséquence, on peut négliger le cisaillement ;
l'épaisseur est faible ; en conséquence, les contraintes dans le sens de l'épaisseur sont supposées nulles ;
on reste en petites déformations.

Déplacement

Déplacement du feuillet moyen (gauche) et d'une fibre normale (droite)

Soit un point M(x, y, z) de la plaque au repos. À l'instant t, sa position est M’, et l'on définit le vecteur déplacement

$\overrightarrow{\mathrm{MM}'} = \begin{pmatrix} u \\ v \\ w \\ \end{pmatrix}$ .

Pour une plaque à un instant donné, les déplacements sur les axes u, v et w sont fonction du point M, donc de ses coordonnées (x, y, z), et de l'instant t.

Par hypothèse, les déplacement verticaux sont les mêmes pour tous les points d'une même fibre normale, on a donc :

w(x, y, z, t) = w(x, y, t).

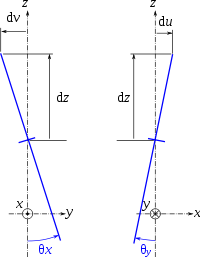
La fibre normale en (x, y) tourne d'un angle θ_x autour de l'axe x et d'un angle θ_y autour de l'axe y. Comme on est en petite déformation, l'arc de cercle décrit par un point lors de la rotation de la fibre normale est assimilable à un segment de droite, et l'on a :

u(x, y, z, t) ≃ z·θ_y(x, y, t) ;

v(x, y, z, t) ≃ -z·θ_x(x, y, t) ;

ou encore

$\begin{matrix} \frac{\partial u}{\partial z} = \theta_y \text{ ;}\\ [1ex] \frac{\partial v}{\partial z} = -\theta_x \text{.}\\ \end{matrix}$

Démonstration

Relation entre θ_x, θ_{y, u et v}

D'après la trigonométrie, on a

$\tan \theta_x = -\frac{\mathrm{d} v}{\mathrm{d} z}$

le signe - vient du fait que l'axe x pointe vers le lecteur, le sens positif est donc le sens antihoraire, ce qui correspond à un déplacement v négatif lorsque z est positif. Et comme on est en petites déformations, θ_x ≪ 1 donc tan θ_x ≃ θ_x.

On a la même chose pour θ_y et u ; le signe + vient du fait que l'axe y pointe à l'opposé du lecteur, le sens positif est donc le sens horaire.

Les angles θ_x et θ_y représentant aussi la pente que prend le feuillet moyen, on a donc également :

$\begin{matrix} \theta_x = \frac{\partial w}{\partial y} \text{ ;}\\ [1ex] \theta_y = -\frac{\partial w}{\partial x} \text{.}\\ \end{matrix}$

Déformation

D'après la définition du tenseur des déformations, on a :

$\left \{ \begin{array}{l} \varepsilon_{11} = \frac{\partial u}{\partial x} = z \cdot \frac{\partial \theta_y}{\partial x} = -z \cdot \frac{\partial^2 w}{\partial x^2} \\ [1ex] \varepsilon_{22} = \frac{\partial v}{\partial y} = -z \cdot \frac{\partial \theta_x}{\partial y} = -z \cdot \frac{\partial^2 w}{\partial y^2} \\ [1ex] \varepsilon_{33} = \frac{\partial w}{\partial z} = 0 \\ [1ex] \varepsilon_{12} = \frac{1}{2} \left ( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right ) = \frac{z}{2} \left ( \frac{\partial \theta_y}{\partial y} - \frac{\partial \theta_x}{\partial x} \right ) = -z \frac{\partial^2 w}{\partial x \partial y} \\ [1ex] \varepsilon_{13} = \frac{1}{2} \left ( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right ) = \frac{1}{2} ( \theta_y - \theta_y ) = 0 \\ [1ex] \varepsilon_{23} = \frac{1}{2} \left ( \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \right ) = \frac{1}{2} ( -\theta_x + \theta_x ) = 0 \\ \end{array} \right .$

soit le tenseur

$[\varepsilon] = \begin{pmatrix} -z \cdot \frac{\partial^2 w}{\partial x^2} & -z \frac{\partial^2 w}{\partial x \partial y} & 0 \\ -z \frac{\partial^2 w}{\partial x \partial y} & -z \cdot \frac{\partial^2 w}{\partial y^2} & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$

On retrouve bien que les cissions ε₁₃ et ε₂₃ sont négligeables, et comme pour les poutres, la déformation varie de manière linéaire selon z : une face est en tension et l'autre est en compression.

Si l'on définit le vecteur des courbures

$\vec{\chi} = \begin{pmatrix} \frac{\partial \theta_y}{\partial x} \\ [1ex] -\frac{\partial \theta_x}{\partial y} \\ [1ex] \frac{1}{2} \left ( \frac{\partial \theta_y}{\partial y} - \frac{\partial \theta_x}{\partial x} \right ) \end{pmatrix} = \begin{pmatrix} -\frac{\partial^2 w}{\partial x^2} \\ [1ex] -\frac{\partial^2 w}{\partial y^2} \\ [1ex] -\frac{\partial^2 w}{\partial x \partial y} \end{pmatrix} = \begin{pmatrix} -\gamma_x \\ [1ex] -\gamma_y \\ [1ex] -\gamma_{xy} \end{pmatrix}$

on a alors

$\begin{pmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{12} \end{pmatrix} = z \cdot \vec{\chi}$ .

On peut définir de manière plus générale le tenseur de courbure

$\mathrm{K} = \begin{pmatrix} \frac{\partial \theta_y}{\partial x} & \frac{1}{2} \left ( \frac{\partial \theta_y}{\partial y} - \frac{\partial \theta_x}{\partial x} \right ) \\ [1ex] \frac{1}{2} \left ( \frac{\partial \theta_y}{\partial y} - \frac{\partial \theta_x}{\partial x} \right ) & - \frac{\partial \theta_x}{\partial y} \end{pmatrix} = \begin{pmatrix} - \frac{\partial^2 w}{\partial x^2} & - \frac{\partial^2 w}{\partial x \partial y} \\ [1ex] - \frac{\partial^2 w}{\partial y \partial x} & - \frac{\partial^2 w}{\partial y^2} \end{pmatrix} = \begin{pmatrix} - \gamma_x & - \gamma_{xy} \\ [1ex] - \gamma_{yx} & - \gamma_y \end{pmatrix}$ .

Le tenseur des déformations sans les termes en z s'écrit donc :

$\begin{pmatrix} \varepsilon_{11} & \varepsilon_{12} \\ \varepsilon_{21} & \varepsilon_{22} \\ \end{pmatrix} = z \cdot \mathrm{K}$ .

Cette écriture met en évidence la linéarité de la déformation en z.

Champ des vitesses

La détermination du champ des vitesses permet d'utiliser les puissances virtuelles en statique (il s'agit alors de vitesses virtuelles), et de résoudre les problèmes de dynamique.

On considère qu'une fibre normale se comporte comme un solide indéformable. On peut donc en chaque point déterminer le torseur cinématique :

$\left \{ \begin{matrix} \omega_x = \frac{\partial \theta_x}{\partial t} = \frac{\partial^2 w}{\partial y \partial t} \\ [1ex] \omega_y = \frac{\partial \theta_y}{\partial t} = -\frac{\partial^2 w}{\partial x \partial t} \\ [1ex] \omega_z = 0 & \text{ (pas de torsion dans le plan)} \\ v_z = \frac{\partial w}{\partial t} \\ \end{matrix} \right .$

Sur le feuillet moyen (w = 0), on a :

v_x = v_y = 0

soit

$\{ \mathcal{V} \} = \begin{matrix}\\ [1ex] \\ [1ex] \\ \end{matrix}_{\mathrm{G}} \begin{Bmatrix} \dot{\theta}_x & 0 \\ [1ex] \dot{\theta}_y & 0 \\ [1ex] 0 & \dot{w} \\ \end{Bmatrix} = \begin{matrix}\\ [1ex] \\ [1ex] \\ \end{matrix}_{\mathrm{G}} \begin{Bmatrix} \frac{\partial^2 w}{\partial y \partial t} & 0 \\ [1ex] -\frac{\partial^2 w}{\partial x \partial t} & 0 \\ [1ex] 0 & \frac{\partial w}{\partial t} \\ \end{Bmatrix}$

Les valeurs de v_x et de v_y à une altitude z quelconque se détermine en transportant le torseur, ou bien en écrivant $\dot{u}(z)$ et $\dot{v}(z)$

$\{ \mathcal{V} \} = \begin{matrix}\\ [1ex] \\ [1ex] \\ \end{matrix}_z \begin{Bmatrix} \dot{\theta}_x & z \dot{\theta}_y \\ [1ex] \dot{\theta}_y & -z \dot{\theta}_x \\ [1ex] 0 & \dot{w} \\ \end{Bmatrix} = \begin{matrix}\\ [1ex] \\ [1ex] \\ \end{matrix}_z \begin{Bmatrix} \frac{\partial^2 w}{\partial y \partial t} & -z \frac{\partial^2 w}{\partial x \partial t} \\ [1ex] -\frac{\partial^2 w}{\partial x \partial t} & -z \frac{\partial^2 w}{\partial y \partial t} \\ [1ex] 0 & \frac{\partial w}{\partial t} \\ \end{Bmatrix}$

Efforts de cohésion et principe d'équivalence

Dans le cas des poutres, on peut définir les efforts de cohésion pour une section complète. Dans le cas des plaques, il faut considérer deux sections perpendiculaires d'un petit élément de matière ; les efforts intérieurs sont donc définis « par mètre ». On peut établir une relation entre le tenseur des contraintes et les efforts de cohésion (principe d'équivalence).

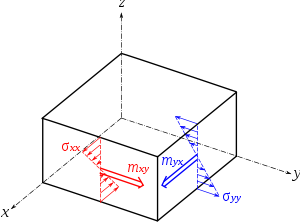
Moments fléchissants

Moments fléchissants et contraintes normales

On peut définir deux moments fléchissants :

le moment fléchissant autour de l'axe y, qui s'exerce donc sur la face normale à x ; il se traduit par une répartition linéaire de la contrainte normale σ_xx :

$m_{xx} = \int_{-h/2}^{h/2} \sigma_{xx} z \mathrm{d} z$ ;
le moment fléchissant autour de l'axe x, qui s'exerce donc sur la face normale à y ; il se traduit par une répartition linéaire de la contrainte normale σ_yy :

$m_{yy} = \int_{-h/2}^{h/2} \sigma_{yy} z \mathrm{d} z$ .

Ils s'expriment en N (Nm/m).

Moments de torsion

Moments de torsion et cission

On peut définir deux moments de torsion :

le moment de torsion autour de l'axe y, qui s'exerce donc sur la face normale à y ; il se traduit par une répartition linéaire de la contrainte de cisaillement τ_yx :

$m_{yx} = \int_{-h/2}^{h/2} \tau_{yx} z \mathrm{d} z$ ;
le moment de torsion autour de l'axe x, qui s'exerce donc sur la face normale à x ; il se traduit par une répartition linéaire de la contrainte de cisaillement τ_xy :

$m_{xy } = \int_{-h/2}^{h/2} \tau_{xy} z \mathrm{d} z$ .

Ils s'expriment également en N (Nm/m).

Efforts tranchants

Efforts tranchants et cission

On peut définir deux efforts tranchants :

l'effort tranchant sur la face normale à y ; il se traduit par une répartition linéaire de la contrainte de cisaillement τ_yz :

$q_{y} = \int_{-h/2}^{h/2} \tau_{yz} \mathrm{d} z$ ;
l'effort tranchant sur la face normale à x ; il se traduit par une répartition linéaire de la contrainte de cisaillement τ_xz :

$q_{x} = \int_{-h/2}^{h/2} \tau_{xz} \mathrm{d} z$ .

Ils s'expriment N/m, et sont négligés dans le cas des plaques minces.

Dynamique

Cette théorie permet de déterminer la propagation des ondes dans les plaques, ainsi que l'étude des ondes stationnaires et des modes vibratoires. Les illustrations ci-dessous montrent quelques modes vibratoires d'une peau de tambour (plaque circulaire).

mode k = 0, p = 1
mode k = 0, p = 2
mode k = 1, p = 2

Déformation de membrane

Théorie des plaques épaisses

Dans la théorie des plaques épaisses, ou théorie de Reissner et Mindlin, la fibre normale reste toujours rectiligne, mais n'est plus nécessairement perpendiculaire au plan moyen. Si θ_x et θ_y désignent les angles que fait la fibre normale avec l'axe z, ils ne correspondent plus à l'inclinaison du plan moyen, on a donc

$\begin{matrix} \theta_x \neq \frac{\partial w}{\partial y} \text{ ;}\\ [1ex] \theta_y \neq -\frac{\partial w}{\partial x} \text{.}\\ \end{matrix}$

Concernant le champ de déformation, les termes gardent leur forme générale

$\left \{ \begin{array}{l} \varepsilon_{11} = z \cdot \frac{\partial \theta_y}{\partial x} \\ [1ex] \varepsilon_{22} = -z \cdot \frac{\partial \theta_x}{\partial y} \\ [1ex] \varepsilon_{33} = 0 \\ [1ex] \varepsilon_{12} = \frac{z}{2} \left ( \frac{\partial \theta_y}{\partial y} - \frac{\partial \theta_x}{\partial x} \right ) \\ [1ex] \end{array} \right .$

et par ailleurs, ε₁₃ et ε₂₃ ne sont plus nuls :

$\left \{ \begin{array}{l} \varepsilon_{13} = \frac{1}{2} \left ( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right ) = \frac{1}{2} \left ( \theta_y + \frac{\partial w}{\partial x} \right ) \\ [1ex] \varepsilon_{23} = \frac{1}{2} \left ( \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \right ) = \frac{1}{2} \left ( -\theta_x + \frac{\partial w}{\partial y} \right ) \\ \end{array} \right .$ ,

On ne peut donc plus négliger le cisaillement.

Les vecteur et tenseur des courbures ne peuvent plus se simplifier et restent :

et l'on a toujours

$\begin{pmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{12} \end{pmatrix} = z \cdot \vec{\chi}$ et : $\begin{pmatrix} \varepsilon_{11} & \varepsilon_{12} \\ \varepsilon_{21} & \varepsilon_{22} \\ \end{pmatrix} = z \cdot \mathrm{K}$ .

Notes

↑ A. E. H. Love, On the small free vibrations and deformations of elastic shells, Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 p. 491–549.
↑ R. D. Mindlin, Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates, Journal of Applied Mechanics, 1951, Vol. 18 p. 31–38.

Voir aussi

Liens externes

Sur les autres projets Wikimedia :

« Théorie des plaques », sur Wikimedia Commons (ressources multimédia)

Cours des Mines de Paris (licence Creative Commons)
Flexion de la bande homogène isotrope à bords libres et du rectangle à deux bords parallèles appuyés, Jean Leray (1963-1964) (téléchargeable en PDF et DjVu)
[PDF] Cours de l'EPFL, P. Lestuzzi
Théorie des plaques élastiques, M. François, Librecours.org
Vibrations de flexion de plaques, L. Jaouen, Université de Sherbrooke
Théorie des plaques élastiques, département Architecture, géologie, environnement & constructions de l'Université de Liège
Calcul statique linéaire pour coques, Guide de validation des progiciels de calcul de structure, ICAB
application au génie civil et à la construction :
- Application aux panneaux de bois
- Application aux structures gonflables
application à l'acoustique :
- [PDF] Entendre la forme d’un tambour, Laboratoire de physique des solides d'Orsay, Images de la physique éd. CNRS
- (en) [PDF] Study of a dome shaped PVDF loudspeaker, application à la membrane d'un haut-parleur, Université du Maine

Portail des sciences des matériaux

Catégorie :

Résistance des matériaux

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorie des plaques de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorie des poutres — Pour les articles homonymes, voir Poutre. La théorie des poutres, ou théorie d Euler Bernoulli, est un modèle utilisé dans le domaine de la résistance des matériaux. Le terme de « poutre » désigne un objet dont la longueur est grande… … Wikipédia en Français
TECTONIQUE DES PLAQUES — La tectonique des plaques est née en 1968 sous la forme d’une théorie de l’évolution de la surface du globe dans son entier, d’où le nom qu’on lui donne souvent de tectonique globale. Fondée sur une approche géophysique, elle a, depuis lors, été… … Encyclopédie Universelle
Tectonique des plaques — Carte des plaques tectoniques terrestres. Âge des plaques … Wikipédia en Français
Techtonique des plaques — Tectonique des plaques Carte des plaques tectoniques terrestres … Wikipédia en Français
SÉISMES ET SISMOLOGIE - Sismicité et tectonique des plaques — Le développement des réseaux de sismographes à l’échelle mondiale a rapidement montré que la sismicité n’était pas distribuée au hasard, mais qu’elle s’articulait le long de grandes lignes sismiques continues à la surface du globe.… … Encyclopédie Universelle
Théorie d'Euler-Bernoulli — Théorie des poutres Pour les articles homonymes, voir Poutre. La théorie des poutres, ou théorie d Euler Bernoulli, est un modèle utilisé dans le domaine de la résistance des matériaux. Le terme de « poutre » désigne un objet dont la… … Wikipédia en Français
Théorie du second gradient — La théorie du second gradient est une théorie permettant de modéliser la puissance des efforts intérieurs dans un milieu continu en supposant qu elle s exprime à l aide d une densité de puissance qui est une forme linéaire du second gradient du… … Wikipédia en Français
Plaques — Plaque Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Theorie de l'expansion terrestre — Expansion terrestre Mouvements des continents au fur et à mesure de l expansion de la Terre. à gauche: Océan Atlantique droite: Océan Pacifique. L expansion terrestre est une théorie essayant d expliquer la position et le mouvement des continents … Wikipédia en Français
Plaques d'or — Reproduction des plaques d or d après la description de Joseph Smith, Musée d Histoire de l Eglise Selon la théologie de l Eglise de Jésus Christ des saints des derniers jours, les plaques d or, également appelées dans une certaine littérature du … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorie des plaques

Sommaire

Historique

Démarche

Définitions et hypothèses