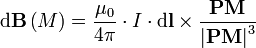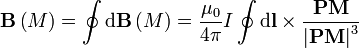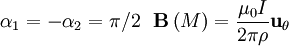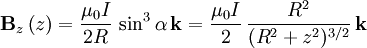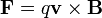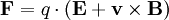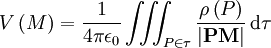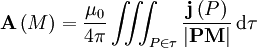Magnetostatique

Magnétostatique

La magnétostatique est l'étude des phénomènes magnétiques pour lesquels le champ magnétique est statique, c’est-à-dire ne dépend pas du temps.

Un champ magnétique statique se rencontre dans les cas de figure suivants :

lorsque le déplacement de charges électriques forme un courant électrique ne dépendant pas du temps : on dit aussi que le courant est constant, ou continu ;
lorsque le champ magnétique est produit par un aimant permanent comme par exemple un matériau ferromagnétique immobile.

Sommaire

1 Champ magnétique produit par un courant constant
- 1.1 Exemples
2 Force magnétique
- 2.1 Potentiel vectoriel magnétique
3 Voir aussi

Champ magnétique produit par un courant constant

La valeur du champ créé en un point M de l'espace par un élément conducteur dl au point P parcouru par un courant constant I est donnée par la loi de Biot et Savart :

$\mathrm{d}\mathbf{B}\left( M \right) = \frac{\mu_0 }{4\pi}\cdot I\cdot \mathrm d \mathbf{l} \times \frac{\mathbf{PM}}{\left| \mathbf{PM} \right|^3}$

avec B le champ magnétique, $μ 0$ une constante appelée perméabilité du vide qui vaut, par définition, dans le système international : $4π10 - 7$ H/m (Henry/mètre) et 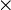$\times$ indique le produit vectoriel.

Il convient alors d'effectuer la sommation sur tous les éléments de courant I dl des :

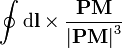$\mathbf B \left( M \right)=\oint \mathrm d \mathbf B \left( M \right)=\frac{\mu_0 }{4\pi}I \oint \mathrm d \mathbf{l} \times \frac{\mathbf{PM}}{\left| \mathbf{PM} \right|^3}$

$\oint \mathrm d \mathbf{l} \times \frac{\mathbf{PM}}{\left| \mathbf{PM} \right|^3}$ est une quantité purement géométrique.

On démontre alors deux propriétés importantes du champ magnétique B en magnétostatique :

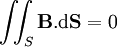$\iint_S \mathbf B. \mathrm d\mathbf S = 0$ pour toute surface S fermée : le champ B est dit à flux conservatif ;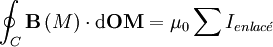
$\oint_C \mathbf B \left( M \right) \cdot \mathrm d \mathbf{OM} = \mu_0 \sum I_{{enlac\acute{e}}}$

avec

B le champ magnétique ;

dOM l'élément linéique de la boucle fermée C ;

I le courant qui traverse la surface S fermée par la boucle C ;

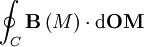$\oint_C \mathbf B \left( M \right) \cdot \mathrm d \mathbf{OM}$ désigne l'intégrale curviligne (ou circulation) le long de la boucle fermée C.

Cette dernière relation est appelée théorème d'Ampère. En utilisant le théorème de Stokes, on peut exprimer ces propriétés sous forme locale : elles forment deux des quatre équations de Maxwell. On a :

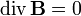$\mathrm{div} \, \mathbf B = 0$ (équation de Maxwell-Φ) ;
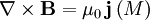$\mathbf \nabla \times \mathbf B = \mu_0\,\mathbf j \left( M \right)$ (équation de Maxwell-Ampère) avec :

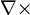$\nabla \times$ l'opérateur rotationnel ;

j le vecteur densité de courant.

Si les courants électriques sont dans un espace fini, l'intensité du champ B décroît à l'infini comme O(1/r³). Ceci et les deux lois locales précédentes, permet grâce au théorème d'Helmholtz de retrouver la loi de Biot et Savart: on peut donc les prendre pour base de la magnétostatique.

L'unité de champ magnétique, le Tesla noté T, est très grande. Le Weber (W) vaut un T.m² et via la loi de Faraday un Volt.s : donc 1 T = 1 V.s/m².

Exemples

Champ d'un segment de fil parcouru par un courant I :

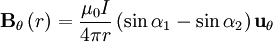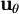$\mathbf B_\theta \left( r \right) = \frac{\mu_0 I}{4\pi r}\,(\sin{\alpha_1} -\sin{\alpha_2})\,\mathbf u_\theta$ où $\mathbf u_\theta$ est le vecteur tangentiel.

Cas d'un fil infini :

$\alpha_1=-\alpha_2=\pi/2\ \ \mathbf B \left( M \right) = \frac{\mu_0 I}{2\pi \rho}\mathbf u_\theta$

Champ créé sur l'axe d'une spire circulaire de rayon R :

$\mathbf B_z \left( z \right) = \frac{\mu_0 I}{2R}\,\sin^3\alpha\,\mathbf k =\frac{\mu_0 I}{2}\,\frac{R^2}{(R^2+z^2)^{3/2}}\,\mathbf{k}$

On a ainsi, par linéarité, dans un solénoïde infiniment long :

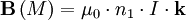$\mathbf{B} \left( M \right) = \mu_0 \cdot n_1 \cdot I\cdot \mathbf{k}$ si M est intérieur, le champ étant nul à l'extérieur. La quantité n₁ désigne le nombre de spires par unité de longueur.

Pour une très petite spire, on peut parler de moment magnétique :

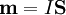
$\mathbf m = I \mathbf S$

$\mathbf B = \frac{\mu_0}{4 \pi} \mathbf \nabla \times \left[ \mathbf m \times \frac{\mathbf r}{ \left| \mathbf r \right|^3}\right]$ , r étant non nul.

Voir aussi le champ d'une spire de courant et autres distributions magnétostatiques

Force magnétique

Une charge électrique q se déplaçant dans un champ magnétique 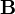$\mathbf{B}$ subit la force de Lorentz :

$\mathbf {F} = q \mathbf{v} \times \mathbf{B}$

où v est la vitesse (au sens vectoriel) de cette charge.

Si un champ électrique E se superpose au champ magnétique, la force qui s'exerce sur la charge est la somme des forces électrique et magnétique :

$\mathbf {F} = q\cdot (\mathbf {E} + \mathbf{v} \times \mathbf{B})$

Cette force peut paraître étrange par son caractère « apparemment » non galiléen : en fait, il n'en est rien, elle s'accorde au contraire très bien à la relativité restreinte.

Potentiel vectoriel magnétique

D'après les équations de Maxwell : div B = 0. Ainsi, le champ B dérive d'un potentiel vecteur A :

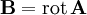$\mathbf{B}=\mathbf{\nabla} \times \mathbf{A}$ (ou bien $\mathbf{B}=\mathrm{rot} \, \mathbf{A}$ )

On a par ailleurs, avec l'équation de Maxwell-Ampère en statique :

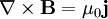$\mathrm{\nabla} \times \mathbf{B}= \mu_0 \mathbf{j}$ , donc

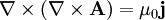$\mathrm{\nabla} \times \left( \mathrm{\nabla} \times \mathbf{A} \right) = \mu_0 \mathbf{j}$ soit encore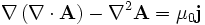

$\mathrm{\nabla} \left( \mathrm{\nabla} \cdot \mathbf{A} \right) - \mathbf \nabla^2 \mathbf{A} = \mu_0 \mathbf{j}$

En adoptant la jauge de Lorenz :

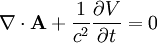$\mathrm{\nabla} \cdot \mathbf{A} + \frac{1}{c^2} \frac{\partial V}{\partial t}=0$ , soit en statique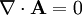

$\mathrm{\nabla} \cdot \mathbf{A}=0$

on a ainsi :

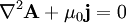$\mathrm{\nabla}^{2} \mathbf{A} + \mu_0 \mathbf{j} = 0$ : le potentiel vecteur vérifie l'équation de Poisson.

Or, dans le cas de l'électrostatique on avait l'équation de Poisson 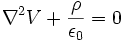$\nabla^{2} V + \frac{\rho}{\epsilon_0} = 0$ et la solution de cette équation pour une distribution localisée de charge est :

$V \left( M \right) = \frac{1}{4\pi \epsilon_0}\iiint_{P\in\tau} \frac{\rho \left( P \right)}{\left| \mathbf{PM} \right|}\, \mathrm d \tau$

Le potentiel vecteur en un point M de l'espace pour une distribution localisée au volume $τ$ est donc par analogie l'intégrale sur le volume :

$\mathbf{A} \left( M \right)=\frac{\mu_0}{4\pi}\iiint_{P\in\tau} \frac{\mathbf{j} \left( P \right)}{\left|\mathbf{PM} \right|} \, \mathrm d\tau$

C'est la formule de Biot et Savart.

Voir aussi

Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Électrostatique : Champ électrique • Charge électrique • Loi de Coulomb • Potentiel électrique
Magnétostatique : Champ magnétique • Moment magnétique • Loi de Biot et Savart
Électrocinétique : Champ électromagnétique • Courant de déplacement • Courant électrique • Ampère • Équations de Maxwell • Force électromotrice • Force de Lorentz • Induction électromagnétique • Loi de Lenz-Faraday • Rayonnement électromagnétique
Magnétisme : Diamagnétisme • Paramagnétisme • Superparamagnétisme • Ferromagnétisme • Antiferromagnétisme • Ferrimagnétisme • Loi de Curie • Domaine de Weiss • Susceptibilité magnétique • Perméabilité magnétique

Portail de la physique
Portail de l’électricité et de l’électronique

Ce document provient de « Magn%C3%A9tostatique ».

Catégories : Article à désacadémiser | Magnétostatique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Magnetostatique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

magnétostatique — ● magnétostatique adjectif Se dit des phénomènes concernant des aimants ou des masses magnétiques au repos. ● magnétostatique nom féminin Science qui étudie ces phénomènes. magnétostatique [maɲetostatik] adj. et n. ÉTYM. Mil. XXe; de magnéto , et … Encyclopédie Universelle
Magnétostatique — Champ magnétique créé par un courant électrique Champ magnétique créé par un aimant … Wikipédia en Français
magnétostatique — magnetostatika statusas T sritis fizika atitikmenys: angl. magnetostatics vok. Magnetostatik, f rus. магнитостатика, f pranc. magnétostatique, f … Fizikos terminų žodynas
Electrostatique Magnétostatique (formulaire) — Électrostatique magnétostatique (formulaire) Cet article fait partie de la série formulaire de physique Optique Électro Magnéstatique Physique quantique Thermodynamique Mécanique des fluides … Wikipédia en Français
Electrostatique magnetostatique (formulaire) — Électrostatique magnétostatique (formulaire) Cet article fait partie de la série formulaire de physique Optique Électro Magnéstatique Physique quantique Thermodynamique Mécanique des fluides … Wikipédia en Français
Électrostatique magnétostatique (formulaire) — Sommaire 1 Electrostatique 1.1 Force électrostatique 1.2 Champ électrostatique 1.3 Champ gradient d un potentiel … Wikipédia en Français
onde magnétostatique — magnetostatinė banga statusas T sritis radioelektronika atitikmenys: angl. magnetic static wave vok. magnetostatische Welle, f rus. магнитостатическая волна, f pranc. onde magnétostatique, f … Radioelektronikos terminų žodynas
onde de volume magnétostatique — tūrinė magnetostatinė banga statusas T sritis radioelektronika atitikmenys: angl. magnetostatic volume wave vok. magnetostatische Raumwelle, f rus. объёмная магнитостатическая волна, f pranc. onde de volume magnétostatique, f … Radioelektronikos terminų žodynas
champ magnétostatique — magnetostatinis laukas statusas T sritis fizika atitikmenys: angl. magnetostatic field vok. magnetostatisches Feld, n; statisches Magnetfeld, n rus. магнитостатическое поле, n pranc. champ magnétique statique, m; champ magnétostatique, m … Fizikos terminų žodynas
énergie magnétostatique — magnetostatinė energija statusas T sritis fizika atitikmenys: angl. magnetostatic energy vok. magnetostatische Energie, f rus. магнитостатическая энергия, f pranc. énergie magnétostatique, f … Fizikos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Magnetostatique

Magnétostatique

Sommaire