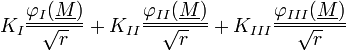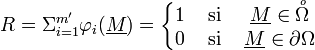Méthode des Eléments Finis Etendus

La Méthode des éléments finis (MEF) est un outil bien maîtrisé actuellement, tant d'un point de vue recherche et développement que d'un point de vue utilisation dans l'industrie. C'est une méthode robuste qui a fait ses preuves, mais les défis d'aujourd'hui et de demain présentent de nouveaux enjeux et trouvent des limites à la MEF. Récemment, le concept d'Éléments Finis Etendus (X-FEM) a été introduit pour tenir compte des problèmes de convergence des éléments finis près d'éventuels singularités du domaine.

Origine

La méthode des X-FEM est la généralisation de méthodes pour traiter la fissuration en éléments finis. La présence de singularités (fissures, perforations, etc...) dégrade fortement la convergence de la MEF, et donc il ne suffit pas de raffiner fortement le maillage à proximité des singularités pour obtenir une bonne solution.

Différentes approches ont été proposées pour pallier ce problème, la plupart reposant sur l'introduction de fonctions capables de représenter ce qu'il se passe au niveau de la fissure, mais souvent ces approches faisaient perdre la bonne prise en compte des conditions aux limites.

En 1996 Babuska et Melenk on introduit un méthode permettant d'avoir les fonctions décrivant la singularité tout en respectant les conditions aux limites. Ils ont montré qu'avec cette méthode, l'on retrouvait le taux de convergence normal.

Principes de base et applications

On sait que les singularités en pointe de fissure peuvent être approchées par :

où r est la distance du point 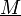à la pointe de fissure.

L'idée principale est donc d'introduire les inconnues 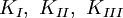et les fonctions de forme 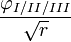, mais ces fonctions n'ont pas les propriétés voulues dans une MEF, notamment sur le bord.

Si l'on a m nœuds pour décrire le domaine, dont 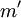sont des nœuds intérieurs, alors grâce à la propriété de partition de l'unité des fonctions de formes EF on a :

On peut donc régulariser (au sens des conditions sur le bord) les fonctions de singularité en les multipliant par R.

L'idée introduite par Babuska et Melenk, est donc d'introduire comme fonction de forme des fonction capables de prendre en compte la singularité que l'on veut traiter (connues par différentes approches matériaux) et de les régulariser sur le bord grâce à la fonction R qui préserve les propriétés des fonctions introduites sur l'intérieur du domaine.

La méthode des X-FEM est une généralisation de cette idée, où l'on s'autorise à enrichir les éléments avec des fonctions régularisées, de manière à pouvoir décrire la répartition spatiale de matière.

Certains pensent qu'il est possible de rentrer toute la complexité d'une structure dans les fonctions de forme, et ainsi faire n'importe quel calcul sur un cube, au lieu de mailler une géométrie compliquée.

Voir aussi

Méthode des éléments finis The Partition of Unity Method (1996), I. Babuska, J. M. Melenk, http://en.scientificcommons.org/165985