Theoremes energetiques

Theoremes energetiques: Théorèmes énergétiques

Les théorèmes énergétiques permettant de poser un problème de mécanique sous forme d'un problème de minimisation, et donc d'utiliser toutes les méthodes existantes pour ce genre de problèmes. Il y a deux théorèmes énergétiques, l'un est beaucoup plus connu que l'autre, il s'agit du théorème de l'énergie potentielle. Le second théorème est similaire au premier, la seule différence étant que dans un cas on parle de l'énergie potentielle et dans l'autre de l'énergie complémentaire.

Sommaire

1 Théorème de l'énergie potentielle

2 Théorème de l'énergie complémentaire

3 Exemples

3.1 Résolution en utilisant le théorème de l'énergie potentielle

3.2 Résolution par l'énergie complémentaire

4 Démonstrations

4.1 A partir de l'erreur en relation de comportement

4.1.1 Établissement de l'expression de l'énergie potentielle et de l'énergie complémentaire

4.1.2 Etude des différents termes de ces expressions

4.1.2.1 Energie potentielle

4.1.2.2 Energie complémentaire

4.1.3 Démonstration des théorèmes énergétiques

4.2 A partir de l'équation d'équilibre local

4.2.1 Énergie potentielle, formulation en déplacement

4.2.2 Énergie complémentaire, formulation en contrainte

Théorème de l'énergie potentielle

Le champ de déplacement solution d'un problème statique de mécanique des milieux continus minimise l'énergie potentielle du milieu.

Théorème de l'énergie complémentaire

Le champ de déplacement solution d'un problème statique de mécanique des milieux continus minimise l'énergie complémentaire du milieu

Exemples

Soit un solide sur un plan sans frottement, relié à un ressort de raideur 'k' et soumis à une force 'F'.

On repère la position de référence du solide par 'x=0', et on suppose que cette position coïncide avec la position de repos (ou longueur à vide) du ressort. On note 'T' la tension du ressort.

Résolution en utilisant le théorème de l'énergie potentielle

L'énergie potentielle du système s'écrit :

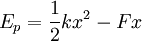
$E_p = \frac{1}{2} k x^2 - F x$

La minimisation de cette énergie donne :

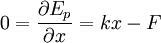
$0=\frac{\partial E_p}{\partial x}=k x -F$

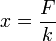
$x=\frac{F}{k}$

Résolution par l'énergie complémentaire

L'énergie complémentaire du système s'écrit :

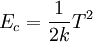
$E_c= \frac{1}{2k}T^2$

Ici comme l'on se doit de chercher 'T' dans l'espace des champs admissibles, on a du fait de l'effort 'F' imposé, 'T' = '-F', et comme on a un problème à 1 ddl, on a la solution.

Démonstrations

A partir de l'erreur en relation de comportement

Établissement de l'expression de l'énergie potentielle et de l'énergie complémentaire

Soit $e$ l'erreur en relation de comportement. Partons de l'expression de $e 2$ . On a :
$e^2\left(\underline{u},\underline{\underline{\sigma}}\right) = \frac{1}{2} \int_\Omega \operatorname{Tr}\left[\left(\underline{\underline{\sigma}} - \underline{\underline{\underline{\underline{K}}}}\cdot \underline{\underline{\varepsilon(u)}}\right) \cdot\underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\left(\underline{\underline{\sigma}}- \underline{\underline{\underline{\underline{K}}}} \cdot\underline{\underline{\varepsilon(u)}}\right)\right] \mathrm d\Omega$ $=\frac{1}{2}\left[ \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot \underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\underline{\underline{\sigma}}\right)\mathrm d\Omega + \int_\Omega \operatorname{Tr}\left(\underline{\underline{\underline{\underline{K}}}}\cdot \underline{\underline{\varepsilon}} \cdot\underline{\underline{\varepsilon}}\right) \mathrm d\Omega - 2 \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot \underline{\underline{\varepsilon}}\right)\mathrm d\Omega \right]$
On applique alors la formule de Green :
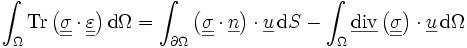
$\int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}} \cdot\underline{\underline{\varepsilon}} \right)\mathrm d\Omega =\int_{\partial\Omega} \left(\underline{\underline{\sigma}}\cdot\underline{n}\right)\cdot\underline{u}\, \mathrm dS -\int_\Omega \underline\operatorname{div} \left(\underline{\underline{\sigma}}\right)\cdot\underline{u}\, \mathrm d\Omega$
On peut séparer l'intégrale sur le bord de $Ω$ en deux intégrales : une sur 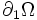$\partial_1\Omega$ , partie de $\partial\Omega$ sur laquelle on a imposé le déplacement et une sur 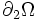$\partial_2\Omega$ , partie de $\partial\Omega$ sur laquelle on a imposé l'effort. On rappelle que dans ce cas on a :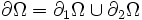
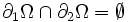
$\partial\Omega=\partial_1\Omega\cup\partial_2\Omega$ et $\partial_1\Omega\cap\partial_2\Omega=\empty$
On obtient donc, en utilisant les équations d'équilibre et les conditions aux limites :
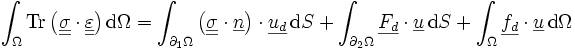
$\int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}} \cdot\underline{\underline{\varepsilon}} \right)\mathrm d\Omega =\int_{\partial_1\Omega} \left(\underline{\underline{\sigma}}\cdot\underline{n}\right)\cdot\underline{u_d}\, \mathrm dS +\int_{\partial_2\Omega} \underline{F_d}\cdot\underline{u}\, \mathrm dS +\int_\Omega \underline{f_d}\cdot\underline{u}\,\mathrm d\Omega$
Soit
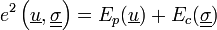
$e^2\left(\underline{u},\underline{\underline{\sigma}}\right) = E_p(\underline{u}) + E_c(\underline{\underline{\sigma}})$
Avec :

$E_p(\underline{u})=\frac{1}{2} \int_\Omega \operatorname{Tr}\left(\underline{\underline{\underline{\underline{K}}}}\cdot\underline{\underline{\varepsilon}} ^2\right) \mathrm d\Omega - \left(\int_\Omega \underline{f_d}\cdot\underline{u}\,\mathrm d\Omega + \int_{\partial_2\Omega} \underline{F_d}\cdot\underline{u}\, \mathrm dS\right)$
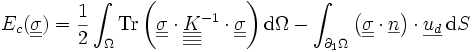
$E_c(\underline{\underline{\sigma}})= \frac{1}{2} \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot\underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\underline{\underline{\sigma}}\right)\mathrm d\Omega - \int_{\partial_1\Omega} \left(\underline{\underline{\sigma}}\cdot\underline{n}\right)\cdot\underline{u_d}\, \mathrm dS$

Etude des différents termes de ces expressions

Energie potentielle
$\frac{1}{2} \int_\Omega \operatorname{Tr}\left(\underline{\underline{\underline{\underline{K}}}}\cdot\underline{\underline{\varepsilon}} ^2\right) \mathrm d\Omega$
est l'énergie de déformation exprimée en déplacement. C'est l'analogue de l'énergie de déformation élastique d'un ressort $\tfrac{1}{2} k (l-l_0)^2$ . C'est une forme bilinéaire symétrique continue et coercive.
$\left(\int_\Omega \underline{f_d}\cdot\underline{u}\,\mathrm d\Omega + \int_{\partial_2\Omega} \underline{F_d}\cdot\underline{u}\, \mathrm dS\right)$
est le travail des efforts imposés (donc connues) dans le champ de déplacement inconnu. C'est une forme linéaire continue.

Energie complémentaire
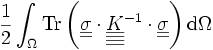
$\frac{1}{2} \int_\Omega \operatorname{Tr}\left(\underline{\underline{\sigma}}\cdot\underline{\underline{\underline{\underline{K}}}}^{-1} \cdot\underline{\underline{\sigma}}\right)\mathrm d\Omega$
est l'énergie de déformation exprimée en contrainte, c'est l'analogue de l'énergie de déformation élastique d'un ressort exprimée en fonction de la force 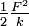$\tfrac{1}{2}\tfrac{F^2}{k}$ . C'est une forme bilinéaire symétrique continue et coercive.
$\int_{\partial_1\Omega} \left(\underline{\underline{\sigma}}\cdot\underline{n}\right)\cdot\underline{u_d}\, \mathrm dS$
est le travail des efforts inconnus dans le champ de déplacement imposé (donc connu) $E p (u)$ ne dépendant que de $u$ et des forces imposées. C'est une forme linéaire continue.

Démonstration des théorèmes énergétiques

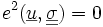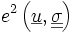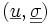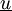Nous savons que la solution exacte est telle que $e^2(\underline{u},\underline{\underline{\sigma}})=0$ , donc elle réalise un minimum de cette fonction. 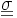De plus comme $e^2\left(\underline{u},\underline{\underline{\sigma}}\right)$ est la somme de deux fonctions de variables indépendantes, le couple $(\underline{u},\underline{\underline{\sigma}})$ est tel que $\underline{u}$ réalise le minimum de $E_p(\underline{u})$ et $\underline{\underline{\sigma}}$ réalise le minimum de $E_c(\underline{\underline{\sigma}})$ .

De plus nous sommes dans les hypothèses d'application du théorème de Stampacchia qui garantit l'existence et l'unicité des solutions de chacun de ces problèmes de minimisation.

De plus le déplacement et la contrainte étant liés par la relation de comportement, on peut choisir de minimiser l'une ou l'autre de ces énergies pour obtenir le couple solution.

A partir de l'équation d'équilibre local

On peut faire des formulations variationnelles en déplacement v CA0 (ci dessous) ou contrainte to CA 0 et obtenir a(u,v)=l(v) ou a(sigma, to)=l(to) équations à solutionner.

Énergie potentielle, formulation en déplacement

on cherche 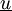$\underline{u}$ , cinématiquement admissible, solution de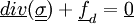
$\underline{div}(\underline{\underline{\sigma}})+\underline{f}_d=\underline{0}$
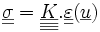
vérifiant la relation de comportement $\underline{\underline{\sigma}}=\underline{\underline{\underline{\underline{K}}}}.\underline{\underline{\varepsilon}}(\underline{u})$

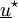On multiplie par un champ cinématiquement admissible à zéro $\underline{u}^\star$ :
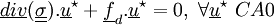
$\underline{div}(\underline{\underline{\sigma}}).\underline{u}^\star+\underline{f}_d.\underline{u}^\star=0,\ \forall \underline{u}^\star \ CA0$

Un intégration donne :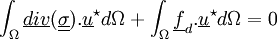
$\int_{\Omega}\underline{div}(\underline{\underline{\sigma}}).\underline{u}^\star d\Omega+\int_{\Omega}\underline{f}_d.\underline{u}^\star d\Omega=0$
La formule de Green permet d'arriver à :
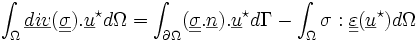
$\int_{\Omega}\underline{div}(\underline{\underline{\sigma}}).\underline{u}^\star d\Omega=\int_{\partial\Omega}(\underline{\underline{\sigma}}.\underline{n}).\underline{u}^\star d\Gamma-\int_{\Omega}\sigma:\underline{\underline{\varepsilon}}(\underline{u}^\star)d\Omega$
Soit:
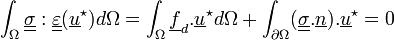
$\int_{\Omega}\underline{\underline{\sigma}}:\underline{\underline{\varepsilon}}(\underline{u}^\star) d\Omega = \int_{\Omega}\underline{f}_d.\underline{u}^\star d\Omega + \int_{\partial\Omega}(\underline{\underline{\sigma}}.\underline{n}).\underline{u}^\star=0$
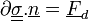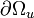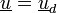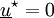
On décompose le bord du domaine en deux: lieux à efforts imposés ${\partial\Omega}_F$ : $\partial\underline{\underline{\sigma}}.\underline{n}=\underline{F}_d$ , lieu à déplacements imposés ${\partial\Omega}_u$ : $\underline{u}=\underline{u}_d$ et $\underline{u}^\star=0$

On obtient alors :
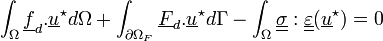
$\int_{\Omega}\underline{f}_d.\underline{u}^\star d\Omega + \int_{{\partial\Omega}_F}\underline{F}_d.\underline{u}^\star d\Gamma -\int_{\Omega}\underline{\underline{\sigma}}:\underline{\underline{\varepsilon}}(\underline{u}^\star)=0$
En utilisant la relation de comportement, on aboutit au problème suivant :

trouver 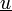$\underline{u}$ cinématiquement admissible tel que :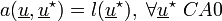

$a(\underline{u},\underline{u}^\star)=l(\underline{u}^\star),\ \forall \underline{u}^\star \ CA0$

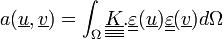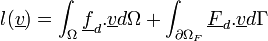
Avec $a(\underline{u},\underline{v})=\int_{\Omega} \underline{\underline{\underline{\underline{K}}}}.\underline{\underline{\varepsilon}}(\underline{u})\underline{\underline{\varepsilon}}(\underline{v})d\Omega$ et $l(\underline{v})=\int_\Omega \underline{f}_d.\underline{v}d\Omega + \int_{{\partial\Omega}_F} \underline{F}_d.\underline{v}d\Gamma$

On peut alors vérifier que l'on est dans le cadre d'application des théorèmes de Lax-Milgram et de Stampacchia, qui assurent d'une part, l'existence et l'unicité de la solution, d'autre par l'équivalence de ce problème au problème de minimisation de la fonctionnelle 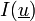$I(\underline{u})$ définie par :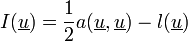

$I(\underline{u})=\frac{1}{2} a(\underline{u},\underline{u}) - l(\underline{u})$

Cette fonctionnelle n'est autre que l'énergie potentielle.

Énergie complémentaire, formulation en contrainte

L'établissement du théorème de l'énergie complémentaire se fait de la même façon, mais en posant une formulation variationnelle en contrainte, pour cela il faut partir de la relation de comportement et la multiplier par un champ de contraintes statiquement admissible à zéro.

Portail du génie mécanique

Portail de la physique

Ce document provient de « Th%C3%A9or%C3%A8mes %C3%A9nerg%C3%A9tiques ».

Catégories : Mécanique des milieux continus | Théorème de physique

Contenu soumis à la licence CC-BY-SA. Source : Article Theoremes energetiques de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Théorèmes énergétiques — Les théorèmes énergétiques permettant de poser un problème de mécanique sous forme d un problème de minimisation, et donc d utiliser toutes les méthodes existantes pour ce genre de problèmes. Il y a deux théorèmes énergétiques, l un est beaucoup… … Wikipédia en Français
Erreur En Relation De Comportement — Sommaire 1 Notion d erreur en relation de comportement 1.1 Champs de déplacement cinématiquement admissibles 1.1.1 Champs de déplacement cinématiquement admissibles … Wikipédia en Français
Erreur en relation de comportement — L erreur en relation de comportement est une notion utilisée en mécanique des milieux continus pour quantifier l erreur commise lors de la résolution approchée d un problème régi par des équations d équilibre, des conditions aux limites et une… … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Théorème de Stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. C est un raffinement du théorème de Lax Milgram. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 … Wikipédia en Français
Théorème de stampacchia — Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
Energie complementaire de deformation — Énergie complémentaire de déformation L énergie complémentaire de déformation, parfois désignée par énergie complémentaire, est l énergie de déformation exprimée avec les quantités relatives aux efforts et non aux déplacements. Dans un cadre plus … Wikipédia en Français
Methode des elements finis — Méthode des éléments finis Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode Des Éléments Finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode des éléments finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments finis (les lignes donnent la direction du champ et la couleur son intensité) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Theoremes energetiques

Théorèmes énergétiques

Sommaire

Théorème de l'énergie potentielle

Théorème de l'énergie complémentaire

Exemples

Résolution en utilisant le théorème de l'énergie potentielle

Résolution par l'énergie complémentaire

Démonstrations

A partir de l'erreur en relation de comportement

Établissement de l'expression de l'énergie potentielle et de l'énergie complémentaire

Etude des différents termes de ces expressions

Energie potentielle

Energie complémentaire

Démonstration des théorèmes énergétiques

A partir de l'équation d'équilibre local

Énergie potentielle, formulation en déplacement

Énergie complémentaire, formulation en contrainte

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Theoremes energetiques

Théorèmes énergétiques

Sommaire

Théorème de l'énergie potentielle

Théorème de l'énergie complémentaire

Exemples

Résolution en utilisant le théorème de l'énergie potentielle

Résolution par l'énergie complémentaire

Démonstrations

A partir de l'erreur en relation de comportement

Établissement de l'expression de l'énergie potentielle et de l'énergie complémentaire

Etude des différents termes de ces expressions

Energie potentielle

Energie complémentaire

Démonstration des théorèmes énergétiques

A partir de l'équation d'équilibre local

Énergie potentielle, formulation en déplacement

Énergie complémentaire, formulation en contrainte

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link