Coercivite
- Coercivite
-
Coercivité
Définitions
Une forme bilinéaire est dite coercive sur  (certains auteurs disent plutôt
(certains auteurs disent plutôt  -elliptique) :
-elliptique) : 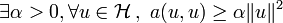
Une fonction f définie sur un espace normé X est dite coercive si 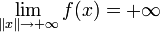 .
.
Lien entre les définitions
Dans le cas ou a est une forme bilinéaire, en posant f(u) = a(u,u) on a équivalence entre la coercivité de a et celle de f. En effet, 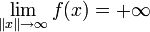 implique qu'il existe R > 0 tel que
implique qu'il existe R > 0 tel que 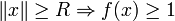 . Ainsi,
. Ainsi,
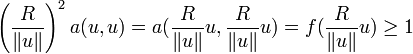
et
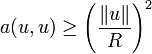 .
.
Cette notion intervient entre autres dans le théorème de Lax-Milgram et la théorie des opérateurs elliptiques, accessoirement dans la méthode des éléments finis.
 Portail des mathématiques
Portail des mathématiques
Catégories : Espace vectoriel normé | Algèbre bilinéaire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Coercivite de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Coercivité — En mathématiques, et plus particulièrement en analyse, une fonction réelle est dite coercive si «elle tend vers l infini à l infini», éventuellement dans une partie spécifiée de l ensemble de départ. Une définition analogue est utilisée pour les… … Wikipédia en Français
Équation de Poisson — Pour les articles homonymes, voir Poisson (homonymie). En analyse vectorielle, l équation de Poisson (ainsi nommée en l honneur du mathématicien et physicien français Siméon Denis Poisson) est l équation aux dérivées partielles du second ordre… … Wikipédia en Français
Lemme de Lax-Milgram — Théorème de Lax Milgram Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Methode des elements finis — Méthode des éléments finis Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode Des Éléments Finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments fin … Wikipédia en Français
Méthode de Galerkin — En mathématiques, dans le domaine de l analyse numérique, les méthodes de Galerkin sont une classe de méthodes permettant de transformer un problème continu (par exemple une équation différentielle) en un problème discret. Cette approche est… … Wikipédia en Français
Méthode des éléments finis — Pour les articles homonymes, voir Élément. Solution bidimensionnelle d une équation magnétostatique obtenue par éléments finis (les lignes donnent la direction du champ et la couleur son intensité) … Wikipédia en Français
Theoreme de Lax-Milgram — Théorème de Lax Milgram Le théorème de Lax Milgram – des noms de Peter Lax et Arthur Milgram – est un théorème de mathématiques. Il est utilisé pour résoudre des équations différentielles partielles via la formulation faible et sert ainsi… … Wikipédia en Français
Theoreme de Stampacchia — Théorème de Stampacchia Le théorème de Stampacchia est un théorème d analyse fonctionnelle. Sommaire 1 Énoncé 2 Démonstration 2.1 Cas général 2.2 Cas symétrique … Wikipédia en Français
 (certains auteurs disent plutôt
(certains auteurs disent plutôt  -elliptique) :
-elliptique) : 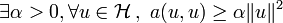
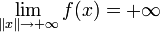 .
.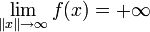 implique qu'il existe R > 0 tel que
implique qu'il existe R > 0 tel que 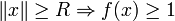 . Ainsi,
. Ainsi,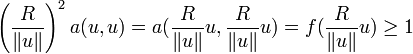
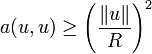 .
.