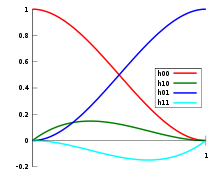
Spline cubique d'Hermite

Spline cubique d'Hermite

On appelle spline cubique d'Hermite une spline de degré 3, nommée ainsi en hommage à Charles Hermite, et dont chaque polynôme Pi(x) se trouve sous la forme suivante:

Les quatre polynômes de base
P_i \in Vect\{h_{00}, h_{10}, h_{01}, h_{11}\}\,

avec

h_{00}(t) = 2t^3-3t^2+1 \,\!
h_{10}(t) = t^3-2t^2+t \,\!
h_{01}(t) = -2t^3+3t^2 \,\!
h_{11}(t) = t^3-t^2 \,\!

ce qui donne le polynôme suivant :

\mathbf{p}(t) = h_{00}(t)\mathbf{p}_0 + h_{10}(t)\mathbf{m}_0 + h_{01}(t)\mathbf{p}_1 + h_{11}(t)\mathbf{m}_1.

Sous cette écriture, il est possible de voir que le polynôme p vérifie:

p(0)=\mathbf{p}_0 \,\!
p(1)=\mathbf{p}_1 \,\!
p'(0)=\mathbf{m}_0 \,\!
p'(1)=\mathbf{m}_1 \,\!

Les splines cubiques d'Hermite sont donc une manière commode de construire un polynôme de degré le plus bas possible interpolant une fonction en 2 points avec ses tangentes[réf. nécessaire].

La courbe est contrôlée par la position des points et des tangentes. La courbe passe par tous les points.

Conséquence : pour trouver le polynôme tel que : P(x_0)=p_0 \;,\; P(x_1)=p_1 \;,\; P'(x_0)=m_0 \;,\; P'(x_1)=m_1

il faut poser : \mathbf{p}(t) = h_{00}(t)\mathbf{p}_0 + h_{10}(t)\mathbf{m}_0 . (x_1-x_0) + h_{01}(t)\mathbf{p}_1 + h_{11}(t)\mathbf{m}_1 .(x_1-x_0).\!

et
\mathbf{P}(t)=\mathbf{p}(\frac{t-x_0}{x_1-x_0})
alors :
\mathbf{P}(x_0)=\mathbf{p}(\frac{x_0-x_0}{x_1-x_0})=\mathbf{p}(0)=p_0
\mathbf{P}(x_1)=\mathbf{p}(\frac{x_1-x_0}{x_1-x_0})=\mathbf{p}(1)=p_1

et  : \mathbf{P}'(x)=\mathbf{p}'(\frac{x-x_0}{x_1-x_0}).\frac{1}{x_1-x_0}

d'où : \mathbf{P}'(x_0)=\mathbf{p}'(\frac{x_0-x_0}{x_1-x_0}).\frac{1}{x_1-x_0}=\mathbf{p}'(0).\frac{1}{x_1-x_0}=m_0.(x_1-x_0) .\frac{1}{x_1-x_0}=m_0
\mathbf{P}'(x_1)=\mathbf{p}'(\frac{x_1-x_0}{x_1-x_0}).\frac{1}{x_1-x_0}=\mathbf{p}'(1).\frac{1}{x_1-x_0}=m_1.(x_1-x_0) .\frac{1}{x_1-x_0}=m_1

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Spline cubique d'Hermite de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Spline cubique d'hermite — On appelle spline cubique d Hermite une spline de degré 3, nommée ainsi en hommage à Charles Hermite, et dont chaque polynôme Pi(x) se trouve sous la forme suivante: avec …   Wikipédia en Français

  • Charles Hermite — Pour les articles homonymes, voir Hermite. Charles Hermite Charles Hermite vers 1901 Naissance …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • FONCTIONS (REPRÉSENTATION ET APPROXIMATION DES) — Il arrive très souvent que, dans les problèmes issus des mathématiques ou des autres sciences, les fonctions qui interviennent soient définies par des procédés qui ne permettent pas d’étudier de manière efficace leurs propriétés. C’est le cas des …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”