Gauß

Carl Friedrich Gauss

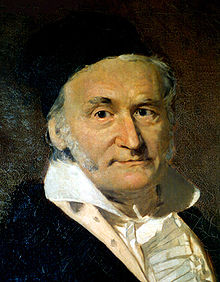
Portrait de Johann Carl Friedrich Gauss (1777-1855), réalisé par Christian Albrecht Jensen
Naissance	30 avril 1777 Brunswick (Saint-Empire romain germanique)
Décès	23 février 1855 (à 77 ans) Göttingen (Royaume de Hanovre)
Nationalité	Allemand
Champs	Astronomie, mathématiques, physique
Institution	Université de Göttingen
Célèbre pour	Travaux en mathématiques et en physique
Distinctions	Médaille Copley Prix Lalande
Signature
modifier

Johann Carl Friedrich Gauß (traditionnellement transcrit Gauss en français) (30 avril 1777 — 23 février 1855) est un mathématicien, astronome et physicien allemand. Doté d'un grand génie, il a apporté de très importantes contributions à ces trois sciences. Surnommé « le prince des mathématiciens », il est considéré comme l'un des plus grands mathématiciens de tous les temps.

La qualité extraordinaire de ses travaux scientifiques était déjà reconnue par ses contemporains. Dès 1856, le roi de Hanovre fit graver des pièces commémoratives avec l'image de Gauss et l'inscription Mathematicorum Principi (« prince des mathématiciens » en latin). Gauss n'ayant publié qu'une partie infime de ses découvertes, la postérité découvrit la profondeur et l'étendue de son œuvre uniquement lorsque son journal intime, publié en 1898, fut découvert et exploité.

Considéré par beaucoup comme distant et austère, Gauss ne travailla jamais comme professeur de mathématiques, détestait enseigner et collabora rarement avec d'autres mathématiciens. Malgré cela, plusieurs de ses étudiants devinrent de grands mathématiciens, notamment Richard Dedekind et Bernhard Riemann.

Gauss était profondément pieux et conservateur. Il soutint la monarchie et s'opposa à Napoléon qu'il vit comme un semeur de révolution.

Sommaire 1 Famille 2 Biographie 3 Reconnaissance 3.1 Prix 3.2 Témoignages 3.3 Fictions 3.4 Portraits, statues 3.5 Utilisation du nom de Gauss 3.6 Utilisation de l'image de Gauss 4 Biographies 5 Notes et références 6 Voir aussi 6.1 Articles connexes 6.2 Liens externes

Famille

• Son grand-père paternel. Paysan pauvre, venu s'établir à Brunswick où il avait un modeste emploi de jardinier. Il eut 3 fils, dont Gerhard, père du mathématicien, fut le deuxième.
• Son grand-père maternel. Tailleur de pierres, il mourut à 30 ans de la tuberculose. Il eut deux enfants : l'ainée Dorothea, la mère du mathématicien, et le cadet, Friedrich, tisserand.
• Ses parents. Modestes et de peu d'instruction, ils se sont mariés en 1776 :
  • Gerhard Dietrich (né en 1744, mort le 14 avril 1808), jardinier, gardien de canal et briqueteur
  • Dorothea Gauß, née Benze (née en 1742, morte le 19 avril 1839 à Göttingen). Elle vint à Brunswick en 1769. Elle passa les vingt dernières années de sa vie dans la maison de son fils. Elle devint aveugle en 1835.
• Sa première femme. Johanna Elisabeth Rosina Osthoff (1780-1809). Le mariage eut lieu le 9 octobre 1805. Ils eurent trois enfants :
  • Joseph^[1] (21 août 1806-1873),
  • Wilhelmina (1808- 12 août 1840). De tous les enfants de Gauss, elle était la plus prédisposée à avoir du génie, mais mourut jeune. Elle avait épousé en 1830 le théologien et linguiste Heinrich Ewald.
  • Louis (11 octobre 1809- 1^er mars 1810).
• Sa deuxième femme. Friederica Wilhelmine Waldeck, « Minna » (1788 - 12 septembre 1831^[2]). Le mariage eut lieu le 4 août 1810. Ils eurent trois enfants :
  • Eugen (29 juillet 1811-1896). Il émigra aux États-Unis en 1832 environ, après une discorde avec son père, pour se retrouver finalement à Saint-Charles, dans le Missouri, où il devint un membre respecté de la communauté.
  • Wilhelm (octobre 1813-1883). Il vint s'installer dans le Missouri, commença comme fermier, se lança dans la vente de chaussures à Saint Louis et devint riche.
  • Therese (juin 1816-1864). À la mort de sa mère en 1831, elle resta à la maison jusqu'à la mort de Gauss, et se maria ultérieurement.

Biographie

Gauss naît le 30 avril 1777 à Brunswick, dans le duché de Brunswick en Allemagne, aujourd'hui dans l'État (Land) de Basse-Saxe. Enfant prodige, il apprend seul à lire et à compter à l'âge de trois ans. À cet âge, il corrige son père qui s'est trompé dans une addition. ^{[réf. nécessaire]}

À l'école, il impressionne très tôt ses professeurs, comme en témoigne l'anecdote suivante^{[réf. nécessaire]} : son professeur, voulant occuper ses élèves agités, leur demande de « calculer la somme de tous les nombres de 1 à 100 ». Pendant que les autres s'affairent à l'addition effective des 100 nombres, le jeune Gauss fournit la réponse correcte en quelques secondes ! Il a astucieusement additionné les nombres extrêmes par paires, remarquant que les 50 sommes donnent toutes le même résultat 101 : 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, etc., 50 + 51 = 101. D'où le résultat demandé, grâce à une seule multiplication : 50 × 101 = 5050.

En 1792, le duc de Brunswick remarque ses aptitudes et lui accorde une bourse afin de lui permettre de poursuivre son instruction. Il est ainsi envoyé au Caroline College, entre 1792 et 1795, où il suit notamment les cours de l'entomologiste Johann Christian Ludwig Hellwig (1743-1831). Durant cette période, il formule la méthode des moindres carrés et une conjecture sur la répartition des nombres premiers, conjecture qui sera prouvée un siècle plus tard^[3]. Gauss acquiert pendant toute sa scolarité une très grande érudition. Et à l'université, il démontre à nouveau, indépendamment, des théorèmes importants.

En 1796, Gauss fait une grande percée, en caractérisant presque complètement tous les polygones réguliers constructibles à la règle et au compas uniquement (Théorème de Gauss-Wantzel), et complétant ainsi le travail commencé par les mathématiciens de l'Antiquité grecque. Satisfait de ce résultat, il demande qu'un polygone régulier de 17 côtés soit gravé sur son tombeau. En 1796 encore, il est le premier à démontrer rigoureusement le théorème fondamental de l'algèbre^[4].

L'année 1801 voit la publication de Disquisitiones arithmeticae, qui contient un exposé très clair sur l'arithmétique modulaire, et qui apporte d'importantes avancées en théorie des nombres, notamment la première preuve de la loi de réciprocité quadratique. Soutenu par des traites du Duc de Brunswick, il n'apprécie pas l'instabilité de cet arrangement, ne croyant pas que les mathématiques soient assez importantes pour mériter une telle aide.

Il est élu le 12 avril 1804 membre de la Royal Society. Le 9 octobre 1805, il célèbre son premier mariage, avec Johanna Osthoff. En 1807, il opte finalement pour une place dans l'astronomie. Il est nommé professeur d'astronomie et directeur de l'observatoire astronomique de Göttingen.

En 1809, il publie un travail d'une importance capitale sur le mouvement des corps célestes qui contient le développement de la méthode des moindres carrés, une procédure utilisée depuis, dans toutes les sciences, pour minimiser l'impact d'une erreur de mesure. Il prouve l'exactitude de la méthode dans l'hypothèse d'erreurs normalement distribuées^[5]. Cette année 1809 est aussi marquée par la mort précoce de sa première femme qu'il aimait, Johanna Osthoff, suivie de près par la mort de l'un de ses enfants, Louis. Gauss plonge dans une dépression, dont il ne sortira jamais entièrement.

En 1810, il se remarie avec « Minna » Waldeck (4 août 1810). Ce mariage ne semble pas avoir été très heureux. Il découvre aussi la possibilité de géométries non-euclidiennes mais ne publiera jamais ce travail^[6].

En 1818, Gauss commence une étude géodésique de l'État de Hanovre, travail qui mènera au développement des distributions normales pour décrire les erreurs de mesure et qui comporte un intérêt dans la géométrie différentielle. Son theorema egregrium permit d'établir une propriété importante de la notion de courbure.

Il mène en 1831 une collaboration fructueuse avec le professeur de physique Wilhelm Weber qui aboutit à des résultats sur le magnétisme, à l'origine de la découverte des lois de Kirchhoff en électricité. Il mène à la construction d'un télégraphe primitif. Il est également l'auteur de deux des quatre équations de Maxwell, qui constituent une théorie globale de l'électromagnétisme. La loi de Gauss pour les champs électriques exprime qu'une charge électrique crée un champ électrique divergent. Sa loi pour les champs magnétiques énonce qu'un champ magnétique divergent vaut 0, c'est-à-dire qu'il n'existe pas de monopôle magnétique. Les lignes de champ sont donc obligatoirement fermées.

La même année, après une longue maladie, sa deuxième femme s'éteint. Sa fille Thérèse prend en main les tâches ménagères et s'occupera de son père jusqu'à la fin de sa vie. Le 23 février 1855, il meurt à Göttingen, Hanovre^[7] (Allemagne). Il est enterré au cimetière de Albanifriedhof.

Reconnaissance

Prix

• Prix Lalande, Académie des sciences, France, 1810,
• Médaille Copley, Société royale de Londres, 1838.

Témoignages

• G. Waldo Dunnington, Carl Frederick Gauss : Le Titan de la Science. L'auteur de cette biographie fut pendant toute sa vie un élève de Gauss. Il écrivit de nombreux articles, et cette biographie.

Fictions

• Daniel Kehlmann, Les arpenteurs du monde, trad. Juliette Aubert, Actes Sud, 2007, 298 p.
  Biographie romancée et croisée de Carl Friedrich Gauss et Alexander von Humboldt.

Portraits, statues

• Un buste de Gauss, dont l'auteur est le sculpteur Georg Arfmann, est exposé au temple Walhalla depuis le 12 septembre 2007.

Utilisation du nom de Gauss

• L'astéroïde (1001) Gaussia a été nommé en son honneur.
• L'unité de l'induction magnétique dans l'ancien système d'unités de mesure CGS s'appelait le gauss (G ou Gs). Elle est reliée au tesla (T) par la relation 1 T = 10000 G
• Un cratère de la Lune se nomme Gauss.
• La première expédition allemande vers l'Antarctique fut appelée Expédition Gauss.
• Gaussberg est un volcan découvert par cette expédition.
• La Gauss Tower est une tour d'observation située en Basse-Saxe.
• Un concours canadien de mathématiques est organisé par le Centre for Education in Mathematics and Computing tous les ans en l'honneur de Gauss.
• On trouve dans plusieurs jeux vidéo des armes à accélération magnétique nommées "canon de Gauss" ou "pistolet Gauss". Citons Fallout, Half-life, OGame ou encore Crysis.
• En algèbre, la "méthode de Gauss" sert à résoudre des systèmes de n équations linéaires à n inconnues
• En probabilités, la distribution gaussienne est très fréquemment utilisée, notamment en modélisation.

• En arithmétique, le Théorème de Gauss permet de simplifier ou transférer un problème de divisibilité.
• La constante de Gauss, qui est égale à l'inverse de la moyenne arithmético-géométrique de 1 et de racine carrée de deux.

Utilisation de l'image de Gauss

• Billets de banque : de 1989 à fin 2001, date de l'abandon de la monnaie allemande au profit de l'euro, le portrait de Gauss, avec une courbe de distribution normale, figurait sur les billets de dix deutschemarks.
• Timbres : l'Allemagne en a édité trois en son honneur, un en 1955, et deux en 1977 pour son 200^e anniversaire.

Biographies

• G. Waldo Dunnington, Carl Frederick Gauss : Le Titan de la Science. L'auteur de cette biographie fut pendant toute sa vie un élève de Gauss. Il écrivit aussi de nombreux articles.
• E. T. Bell, Les grands mathématiciens, Payot, 1961. Chapitre XIV : Gauss, le Prince des Mathématiciens.
• Stephen Hawking, Et Dieu créa les nombres, les plus grands textes de mathématiques réunis et commentés par l'auteur, Dunod, 2006, 1172pp. In-8 , illustr. portraits h.t. et figures, rel. cart. Textes et biographies : Euclide, Archimède, Diophante, Descartes, Newton, Laplace, Fourier, Gauss, Cauchy, Boole, Riemann, Dedekind, Cantor, Lebesgue, Gödel, Turing.
• Pour la Science, Les Génies de la science nº 36, Gauss, prince des mathématiques, août-octobre 2008, 96 p.

Notes et références

Voir aussi

Articles connexes

• Conditions de Gauss dans les articles optique géométrique, lentille et miroir.
• Détermination orbitale
• Élimination de Gauss-Jordan, un algorithme de l'algèbre linéaire pour déterminer les solutions d'un système d'équations linéaires, pour déterminer le rang d'une matrice ou pour calculer l'inverse d'une matrice carrée inversible.
• Jacques Quételet, l'un des fondateurs de la statistique
• Loi normale gaussienne en probabilités et statistiques (représentée par la courbe de Gauss)
• Théorèmes de Gauss

Liens externes

• (en) Sur Gauss et son travail
• (en) John J. O'Connor et Edmund F. Robertson, Johann Carl Friedrich Gauss, MacTutor History of Mathematics archive.
• Timbre représentant Gauss
• [http:// www.banknotes.com/de.htm Gauss sur un billet de 10 Marks allemand (aller voir DE-38)]
• Le prince des mathématiques

• Portail de la physique
• Portail des mathématiques
• Portail de l’astronomie