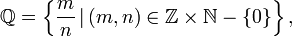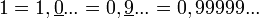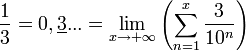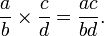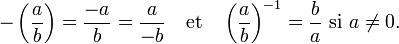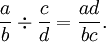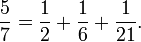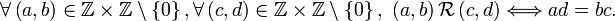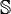ℚ

Nombre rationnel

Un nombre rationnel est, en mathématiques, un nombre qui peut s'exprimer comme le quotient de deux entiers relatifs. Les nombres rationnels non entiers (souvent appelés fractions) sont souvent notés a/b, où a et b sont deux entiers relatifs (avec b non nul). On appelle a le numérateur et b le dénominateur.

Chaque nombre rationnel peut s'écrire d'une infinité de manière différente, comme 1/2=2/4=3/6=etc. Mais il existe une forme privilégiée, quand a et b n'ont pas de diviseurs communs autre que 1 (ils sont premiers entre eux). Tout nombre rationnel non nul possède exactement une seule forme de ce type avec un dénominateur positif. On parle alors de fraction irréductible.

Le développement décimal d'un nombre rationnel est toujours périodique au bout d'une certaine décimale (par exemple dans le cas d'une écriture décimale finie, le rajout de zéros assure la périodicité). Cela est vrai dans n'importe quelle base. Réciproquement, si un nombre possède un développement décimal périodique dans au moins une base, alors c'est un nombre rationnel.

Un nombre réel qui n'est pas rationnel est dit irrationnel. L'ensemble des nombres rationnels est un corps, noté $\mathbb{Q}$ , que l'on peut noter formellement:

$\mathbb{Q} = \left\{\frac{m}{n}\,|\, (m,n) \in \mathbb{Z}\times \mathbb{N}-\{0\} \right\},$

où $\mathbb{Z}$ est l'anneau des entiers.

Développement décimal

Comme tous les réels, les rationnels admettent une représentation en développement décimal illimité. Le développement décimal des nombres rationnels a la particularité d'être périodique. C'est-à-dire qu'il existe un suffixe constitué d'une séquence finie de chiffres se répétant continuellement. Cette séquence est appelée : « période du développement décimal illimité ».

Le développement décimal illimité d'un nombre réel, et a fortiori d'un nombre rationnel, est unique si on s'interdit de finir par une séquence périodique composée de ’9’. En effet, dans ce dernier cas, il existera une écriture équivalente se terminant par une période composée de ’0’, et mieux encore, un développement décimal limité équivalent.

Conventionnellement, lorsque nous écrivons un nombre avec les chiffres arabes dans le système décimal nous traçons, s'il y a lieu, une barre horizontale au-dessous de la séquence périodique. Il est aussi possible de mettre un point au-dessus de chaque chiffre de la période, mais cette notation est beaucoup moins utilisée.

Lorsqu'une période est indiquée nous devons faire référence à un nombre rationnel et c'est pour cette raison que d'une manière rigoureuse :

$1 = 1,\underline{0}... = 0,\underline{9}... = 0,99999...$

$\frac{1}{3} = 0,\underline{3}... = \lim_{x\rightarrow +\infty} \left( \sum_{n=1}^{x} \frac{3}{10^n} \right)$

Le développement décimal illimité d'un nombre rationnel est périodique, et réciproquement, un nombre à développement décimal périodique est toujours rationnel. Ce critère est néanmoins mal commode pour évaluer la rationalité d'un nombre. Un deuxième critère est donnée par la fraction continue. Un nombre est rationnel si et seulement si son développement en fraction continue est fini. Cette méthode est à l'origine des premières démonstrations de l'irrationalité de e la base du logarithme népérien et de π.

Ainsi, le nombre $0,12\,122\,1222\,12222...\,$ (où l'on a des séquences de ’2’ de plus en plus longues) est irrationnel car il n'y a pas de période.

Arithmétique des rationnels

Article détaillé : Fraction (mathématiques)#Opérations sur les fractions.

Deux nombres rationnels a/b et c/d sont égaux si et seulement si ad=bc.

L'addition est donnée par:

$\frac{a}{b} + \frac{c}{d} = \frac{ad+bc}{bd}.$

La multiplication par:

$\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}.$

L'opposé et l'inverse par

$- \left( \frac{a}{b} \right) = \frac{-a}{b} = \frac{a}{-b} \quad\mbox{et}\quad \left(\frac{a}{b}\right)^{-1} = \frac{b}{a} \mbox{ si } a \neq 0.$

On en déduit que le quotient est donné par:

$\frac{a}{b} \div \frac{c}{d} = \frac{ad}{bc}.$

Fraction égyptienne

Article détaillé : Fraction égyptienne.

Tout nombre rationnel positif peut s'exprimer comme somme d'inverses distincts d'entiers naturels. Par exemple, on a :

$\frac{5}{7} = \frac{1}{2} + \frac{1}{6} + \frac{1}{21}.$

Construction formelle

Article détaillé : Construction des nombres rationnels.

On peut voir un entier rationnel comme la classe d'équivalence d'une paire ordonnée d'entiers, par la relation d'équivalence suivante:

$\forall \left(a,b\right) \in \mathbb{Z}\times \mathbb{Z}\setminus\left\{0\right\},\forall \left(c,d\right) \in \mathbb{Z}\times \mathbb{Z}\setminus\left\{0\right\},\ (a,b)\,\mathcal{R}\,(c,d) \Longleftrightarrow ad=bc.$

On note alors 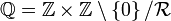$\mathbb{Q}=\mathbb{Z}\times \mathbb{Z}\setminus\left\{0\right\}/\mathcal{R}$ , c'est-à-dire que l'ensemble des nombres rationnels est le quotient de 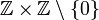$\mathbb{Z}\times \mathbb{Z}\setminus\left\{0\right\}$ par la relation d'équivalence.

On peut ensuite injecter les entiers dans les rationnels, et définir des lois de composition interne pour se donner une structure de corps.

Cette construction est valable à partir de n'importe quel anneau intègre, on parle alors de corps des fractions.

Propriétés

La dénombrabilité des rationnels strictement positifs

L'ensemble $\mathbb{Q}$ , munis des lois d'addition et de multiplication données plus haut, forme un corps, le corps des fractions des entiers $\mathbb{Z}$ .

Les rationnels sont le plus petit corps de caractéristique nulle. Tout autre corps de caractéristique nulle contient une copie de $\mathbb{Q}$ .

La clôture algébrique de $\mathbb{Q}$ , c'est-à-dire le corps des racines des polynômes à coefficients rationnels est l'ensemble des nombres algébriques.

L'ensemble des rationnels est dénombrable. Or par l'argument de la diagonale de Cantor, nous savons que le corps des nombres réels ne l'est pas. On dit alors que les nombres réels sont presque tous irrationnels, au sens de la mesure de Lebesgue. On dit que $\mathbb{Q}$ est un ensemble négligeable.

Topologie

Muni de la valeur absolue, l'ensemble $\mathbb{Q}$ est un espace métrique. Cet ensemble est dense dans l'ensemble des nombres réels, c'est-à-dire que l'adhérence de $\mathbb{Q}$ est $\mathbb{R}$ . Les nombres rationnels ne forment donc pas un espace complet.

Nombre p-adique

On peut munir $\mathbb{Q}$ d'une autre métrique.

Soit $p$ un nombre premier et notons, pour tout entier non nul $a$ :

| a | p = p - n,

où $p n$ est la plus grande puissance de $p$ divisant $a$ .

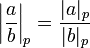Arbitrairement, on pose $| 0 | p = 0$ . Puis pour chaque nombre rationnel $a / b$ , on pose : $\left|\frac{a}{b}\right|_p = \frac{|a|_p}{|b|_p}$ .

Alors 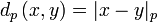$d_p\left(x, y\right) = |x - y|_p$ définit un espace métrique.

L'espace métrique 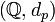$\left(\mathbb{Q}, d_p\right)$ n'est pas complet, et sa complétion est le corps des nombres p-adique $\mathbb{Q}_p$ . Le théorème d'Ostrowski montre que toute valeur absolue non triviale sur $\mathbb{Q}$ est équivalente, soit à la valeur absolue usuelle, soit à une valeur absolue p-adique.

Voir aussi

Liens externes

Le logiciel PC Fraction calcule des fractions égyptiennes, partielles, pythagoréennes, dyadiques (binaires) etc.

Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif