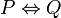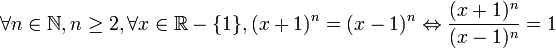Si et seulement si

En logique classique, deux propositions P et Q sont logiquement équivalentes ou équivalentes si P et Q ont simultanément même valeur de vérité; c'est-à-dire que P et Q sont vraies (resp. fausses), dans exactement les mêmes situations. On écrit

Qui se lit :

« P est vraie si et seulement si Q est vraie »

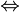«  » est le connecteur d’équivalence dont la table de vérité est donnée ci-dessous :

P	Q	P ⇔ Q
Vrai	Vrai	Vrai
Vrai	Faux	Faux
Faux	Vrai	Faux
Faux	Faux	Vrai

L’équivalence P ⇔ Q n’est autre que (P ⇒ Q) ∧ (Q ⇒ P) ((P implique Q) et (Q implique P)).

En logique intuitionniste, deux propositions P et Q sont équivalentes si et seulement si on a une démonstration de Q à partir de P et une démonstration de P à partir de Q.

Autrement dit, dans les deux cas classique et intuitionniste, dire que deux propositions P et Q sont équivalentes revient à dire que chacune d’elles implique l’autre.

Dans ce cas, les propositions « P ⇒ Q » et « Q ⇒ P » sont dites réciproques l’une de l’autre.

Pour démontrer, une équivalence P ⇔ Q, il faut donc démontrer l’implication P ⇒ Q et sa réciproque.

Dans le langage naturel, pour traduire que deux propositions P et Q sont équivalentes, on dira indifféremment :

• P est vraie si et seulement si Q est vraie.
• Pour que P soit vraie, il faut et il suffit que Q soit vraie.
• Une condition nécessaire et suffisante pour que P soit vraie est que Q soit vraie (ou cns).
• La vérité de P est une condition nécessaire et suffisante pour que Q soit vraie.
• P équivaut à Q.

D’autres expressions « ou encore », « ou » (mais pas le connecteur logique ou), « soit » peuvent traduire une équivalence comme dans l’exemple suivant :

Pour tout réel x, x²=x équivaut à x²-x=0 soit x(x-1)=0 ou encore ((x=0) ou (x=1))

Ici, « soit » (XOR) ne sert pas à définir un objet, et le dernier « ou » est un ou logique (OR).

ssi ((en) iff) est une abréviation de « si et seulement si » couramment utilisée pour écrire des équivalences.

Propriétés

• P ⇔ P (l'équivalence est réflexive)
• (P ⇔ Q) ⇒ (Q ⇔ P) (l'équivalence est symétrique)
• (P ⇔ Q) ∧ (Q ⇔ R) ⇒ (P ⇔ R) (l’équivalence est transitive)

Ces trois lois montrent que l'équivalence logique est une relation d'équivalence

• ¬¬P ⇔ P (Dans la logique classique, ceci équivaut au principe du tiers exclu)
• (P ⇔ Q) ⇔ (¬P ⇔ ¬Q) (contraposition)

Exemples

• On a

• L’équivalence ∀x, y∈ℝ (x=y ⇔ x²=y²) (en élevant au carré) est fausse parce que par exemple 2²=(-2)² n’implique pas 2=-2
• L’équivalence suivante est vraie

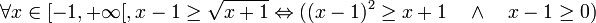(en élevant au carré)

En élevant au carré, on perd l’information que x-1 est supérieur à une racine carrée et doit être positif et pour avoir l’équivalence, on rajoute la propriété x-1≥0.

Remarques :

Démontrer par équivalence n’est pas toujours simple ; dans certains cas, il est préférable de démontrer séparément les implications réciproques.

Dire que l’équivalence P ⇔ Q est vraie ne veut pas dire que P et Q sont vraies, mais que si l’une d’entre elles est vraie (resp. fausse), l’autre aussi.

Équivalence entre plusieurs propositions

Soient trois propositions P, Q et R.

Pour démontrer les équivalences P ⇔ Q ⇔ R, il suffit de démontrer les implications :

P ⇒ Q, Q ⇒ R et R ⇒ P.

Soient les implications P ⇒ Q, Q ⇒ R et R ⇒ P établies.

Pour démontrer que Q ⇒ P, on utilise Q ⇒ R et R ⇒ P.

Pour démontrer que R ⇒ Q, on utilise R ⇒ P et P ⇒ Q.

Et enfin pour démontrer que P ⇒ R, on utilise P ⇒ Q et Q ⇒ R.

Ce type de démonstration s’appelle une démonstration « circulaire » ou « en cercle ».

On peut généraliser à n propositions P₁, P₂… P_n.

Pour démontrer les équivalences P₁ ⇔ P₂ ⇔… ⇔ P_n, il suffit de démontrer les implications :

P₁ ⇒ P₂, P₂ ⇒ P₃… P_n-1 ⇒ P_n et P_n ⇒ P₁.

• Portail des mathématiques
• Portail de la logique