Théorème de gauss-lucas

Théorème de gauss-lucas

Théorème de Gauss-Lucas

Page d'aide sur l'homonymie Pour les articles homonymes, voir Théorème de Gauss.

En mathématiques, le théorème de Gauss-Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont situées dans l'enveloppe convexe de l'ensemble des racines du polynôme d'origine.

Ce résultat est utilisé de façon implicite en 1836 par Carl Friedrich Gauss et prouvé en 1874 par Édouard Lucas[1].

Sommaire

Motivation

Il est facile de remarquer que si 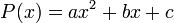P(x) =ax^2+ bx +c \, est un polynôme du second degré, le zéro de 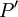P^\prime est la demi-somme des zéros de P\,.

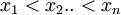Par ailleurs, si un polynôme de degré n\, à coefficients réels admet n\, zéros réels distincts x_1<x_2 ..<x_n\,, on voit en utilisant le théorème de Rolle que les zéros du polynôme dérivé sont dans l'intervalle [x_1,x_n]\,.

Le résultat suivant peut être vu comme une généralisation.

Enoncé

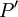Soit P\, un polynôme non constant à coefficients complexes. Alors tout zéro de P^\prime appartient à l'enveloppe convexe de l'ensemble des zéros de P\,.

Preuve

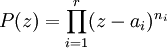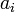Soit P(z)= \prod_{i=1}^r (z-a_i)^{n_i} la décomposition de P\, en facteurs irréductibles : les complexes a_i\, sont les zéros distincts du polynôme, les entiers 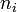n_i\, leurs multiplicités.

On a alors

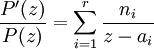
\frac{P^\prime(z)}{P(z)}= \sum_{i=1}^r\frac{n_i}{z-a_i}

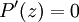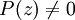En particulier, si P^\prime(z)=0 et P(z)\not=0,

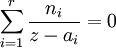\sum_{i=1}^r\frac{n_i}{z-a_i}=0\ ou encore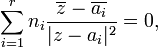 \ \sum_{i=1}^rn_i\frac{\overline{z}-\overline{a_i} } {\vert z-a_i\vert^2}=0,

ce qui s'écrit aussi

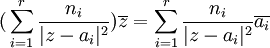
\big(\sum_{i=1}^r\frac{n_i}{\vert z-a_i\vert^2}\big)\overline{z}= \sum_{i=1}^r\frac{n_i}{\vert z-a_i\vert^2}\overline{a_i}

En prenant les conjugués, on voit que 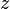z\, est un barycentre à coefficients positifs des a_i\,.

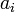Le cas où 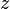z\, est aussi zéro de P\, est évident.

Voir aussi

Notes et références

  1. ↑ Édouard Lucas, Propriétés géométriques des fractions rationnelles, C. R. Acad. Sci. Paris, t. 77 et 78 (1874)
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Gauss-Lucas ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de gauss-lucas de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Theoreme de Gauss-Lucas — Théorème de Gauss Lucas Pour les articles homonymes, voir Théorème de Gauss. En mathématiques, le théorème de Gauss Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont… …   Wikipédia en Français

  • Théorème de Gauss-Lucas — Pour les articles homonymes, voir Théorème de Gauss. En mathématiques, le théorème de Gauss Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont situées dans l enveloppe… …   Wikipédia en Français

  • Théorème de Gauss (électromagnétisme) — Pour les articles homonymes, voir Théorème de Gauss. En électromagnétisme, le théorème de Gauss permet de calculer le flux d un champ électrique à travers une surface compte tenu de la répartition des charges. Il est dû à Carl Friedrich Gauss. Le …   Wikipédia en Français

  • Théorème de Gauss-Markov — En statistiques, le théorème de Gauss–Markov, nommé ainsi d après Carl Friedrich Gauss et Andrei Markov, énonce que dans un modèle linéaire dans lequel les erreurs ont une espérance nulle, sont non corrélées et dont les variances sont égales, le… …   Wikipédia en Français

  • Théorème de Gauss (gravitation) — Pour les articles homonymes, voir Théorème de Gauss. En mécanique, on définit par analogie au Théorème de Gauss de l électromagnétisme une forme du théorème de Gauss appliqué à la gravitation. Le flux du champ de gravitation à travers une surface …   Wikipédia en Français

  • Théorème de Gauss — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs lemmes ou théorèmes portent le nom de Gauss, en référence au mathématicien Carl Friedrich Gauss. Lemmes : un lemme de Gauss en arithmétique …   Wikipédia en Français

  • Théorème de Lucas — Théorème de Gauss Lucas Pour les articles homonymes, voir Théorème de Gauss. En mathématiques, le théorème de Gauss Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont… …   Wikipédia en Français

  • Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… …   Wikipédia en Français

  • Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… …   Wikipédia en Français

  • Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”