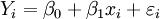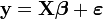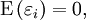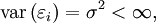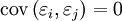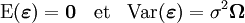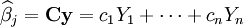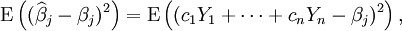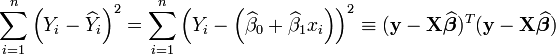Théorème de gauss-markov

Théorème de Gauss-Markov

En statistiques, le théorème de Gauss–Markov, nommé ainsi d'après Carl Friedrich Gauss et Andrei Markov, énonce que dans un modèle linéaire dans lequel les erreurs ont une espérance nulle, sont non corrélées et dont les variances sont égales, le meilleur estimateur linéaire non biaisé des coefficients est l'estimateur des moindres carrés.

Plus généralement, le meilleur estimateur linéaire non biaisé d'une combinaison linéaire de variables aléatoires est son estimateur par les moindres carrés. On ne suppose pas que les erreurs possèdent une loi normale, ni qu'elles sont indépendantes (seulement non corrélées), ni qu'elles possèdent la même loi de probabilité.

Plus explicitement, supposons que l'on ait :

$Y_i=\beta_0+\beta_1 x_i+\varepsilon_i$

Pour i = 1, . . ., n, où β₀ et β₁ sont des paramètres qui ne sont pas aléatoires mais non-observables, x_i sont des observations, ε_i sont aléatoires, et donc Y_i sont des variables aléatoires. Posons x en minuscule, s'agissant d'une observation ; et Y en majuscule car il s'agit d'une variable aléatoire. Les variables aléatoires ε_i sont appelées "erreurs".

En pratique, il peut y avoir plus de deux variables explicatives (les x plus haut) et on a généralement recours à une écriture matricielle plus concise :

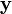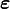$\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}$

avec $\mathbf{y}$ et $\boldsymbol{\varepsilon}$ de dimension n × 1, 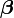$\boldsymbol{\beta}$ de dimension k × 1, et enfin 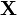$\mathbf{X}$ de dimension n × k.

Le théorème de Gauss–Markov se base sur des hypothèses sur l'espérance et la matrice de variance-covariance des aléas :

${\rm E}\left(\varepsilon_i\right)=0,$
${\rm var}\left(\varepsilon_i\right)=\sigma^2<\infty,$

(c'est-à-dire que toutes les erreurs ont la même variance : on parle d'homoscédasticité) et

${\rm cov}\left(\varepsilon_i,\varepsilon_j\right)=0$

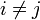pour $i\not=j$ ; ce qui traduit la non-corrélation. Matriciellement, les hypothèses se traduisent ainsi :

$\operatorname{E}( \boldsymbol{\varepsilon} ) = \mathbf{0} \;\;\mbox{ et }\;\;\operatorname{Var}( \boldsymbol{\varepsilon} ) = \sigma^2 \boldsymbol{\Omega}$

où la matrice 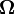$\boldsymbol{\Omega}$ est la matrice identité n × n.

Un estimateur linéaire de β_j est une combinaison linéaire des données observées :

$\widehat{\beta}_j = \mathbf{C}\mathbf{y} = c_1Y_1+\cdots+c_nY_n$

dans laquelle les coefficients c_i ne dépendent pas des précédents coefficients β_i, car ceux-ci ne sont pas observables, mais peuvent dépendre de x_i, car il s'agit des observations.

L'erreur moyenne quadratique d'un tel estimateur est :

${\rm E} \left((\widehat{\beta}_j-\beta_j)^2\right) = {\rm E} \left((c_1Y_1+\cdots+c_nY_n-\beta_j)^2\right),$

c'est-à-dire, l'espérance du carré de la différence entre l'estimateur et les paramètres à estimer. L'erreur moyenne quadratique d'un estimateur coïncide avec sa variance si l'estimateur n'est pas biaisé ; dans le cas contraire, l'erreur moyenne quadratique est la somme de la variance et du carré du biais.

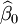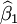Le meilleur estimateur non-biaisé est l'estimateur de plus faible erreur moyenne quadratique (donc ici de plus faible variance). Les estimateurs par les moindres carrés de β₀ et β₁ sont les fonctions $\widehat{\beta}_0$ et $\widehat{\beta}_1$ de Ys et xs qui minimisent la somme des carrés des erreurs de mesure :

$\sum_{i=1}^n\left(Y_i-\widehat{Y}_i\right)^2=\sum_{i=1}^n\left(Y_i-\left(\widehat{\beta}_0+\widehat{\beta}_1 x_i\right)\right)^2 \equiv (\mathbf{y}-\mathbf{X} \boldsymbol{\widehat{\beta}})^T(\mathbf{y}-\mathbf{X} \boldsymbol{\widehat{\beta}})$

Ne pas confondre erreur sur des quantités non-observables et erreurs de mesure sur des grandeurs observables.

Le théorème de Gauss-Markov énonce que, parmi tous les estimateurs linéaires non-biaisés, l'estimateur par moindre carré est le seul à présenter une variance minimale. On peut résumer tout cela en disant que l'estimateur par moindre carré est BLUE^[1] (en anglais : Best Linear Unbiaised Estimator).

En termes de formulation matricielle, la démonstration du théorème de Gauss–Markov est faite en démontrant que la différence entre la matrice de covariance de n'importe quel estimateur linéaire non biaisé et celle de l'estimateur des moindres carrés est une matrice semi-définie positive.

Notes et références

↑ A. C. Aitken, On Least Squares and Linear Combinations of Observations, Proceedings of the Royal Society of Edinburgh, 1935, vol. 55, pp. 42-48.

Voir aussi

Régression linéaire

Portail des probabilités et des statistiques

Ce document provient de « Th%C3%A9or%C3%A8me de Gauss-Markov ».

Catégories : Estimation (statistique) | Carl Friedrich Gauss | Théorème de mathématiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de gauss-markov de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Theoreme de Gauss-Markov — Théorème de Gauss Markov En statistiques, le théorème de Gauss–Markov, nommé ainsi d après Carl Friedrich Gauss et Andrei Markov, énonce que dans un modèle linéaire dans lequel les erreurs ont une espérance nulle, sont non corrélées et dont les… … Wikipédia en Français
Théorème de Gauss-Markov — En statistiques, le théorème de Gauss–Markov, nommé ainsi d après Carl Friedrich Gauss et Andrei Markov, énonce que dans un modèle linéaire dans lequel les erreurs ont une espérance nulle, sont non corrélées et dont les variances sont égales, le… … Wikipédia en Français
Théorème de Gauss-Lucas — Pour les articles homonymes, voir Théorème de Gauss. En mathématiques, le théorème de Gauss Lucas, ou théorème de Lucas, établit une propriété des polynômes complexes. Il énonce que les racines du polynôme dérivé sont situées dans l enveloppe… … Wikipédia en Français
Théorème de Gauss (électromagnétisme) — Pour les articles homonymes, voir Théorème de Gauss. En électromagnétisme, le théorème de Gauss permet de calculer le flux d un champ électrique à travers une surface compte tenu de la répartition des charges. Il est dû à Carl Friedrich Gauss. Le … Wikipédia en Français
Théorème de Gauss (gravitation) — Pour les articles homonymes, voir Théorème de Gauss. En mécanique, on définit par analogie au Théorème de Gauss de l électromagnétisme une forme du théorème de Gauss appliqué à la gravitation. Le flux du champ de gravitation à travers une surface … Wikipédia en Français
Théorème de Gauss — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs lemmes ou théorèmes portent le nom de Gauss, en référence au mathématicien Carl Friedrich Gauss. Lemmes : un lemme de Gauss en arithmétique … Wikipédia en Français
Théorème de d'Alembert-Gauss — Pour les articles homonymes, voir Théorème de Gauss. Jean le Rond D Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l algèbre. Sa motivation est entièrement analytique, il r … Wikipédia en Français
Gauss (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Carl Friedrich Gauss (1777 1855), mathématicien, astronome et physicien allemand. Le gauss, une unité de mesure du champ magnétique, noté G. GAUSS, un… … Wikipédia en Français
Entier de Gauss — Pour les articles homonymes, voir Entier (homonymie). Carl Friedrich Gauss. En mathématiques, et plus précisément en théorie algébrique des nombres, un entier de … Wikipédia en Français
Carl Friedrich Gauss — « Gauss » redirige ici. Pour les autres significations, voir Gauss (homonymie). Carl Friedrich Gauß Portrait de Johann Carl Friedrich Gauss (1777 1855), réalisé par Christian … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de gauss-markov