Théorème de burnside (groupe résoluble)

Fixons les notations, G est un groupe noté multiplicativement et l'élément neutre est noté 1, p et q désigne des nombres premiers et n et m des nombres positifs.

Raisonnons par l'absurde. G désigne maintenant un groupe d'ordre pⁿ.q^m non résoluble. Choisissons le couple (n, m) tel qu'il soit minimal.

• G est un groupe simple, non abélien et n et m sont différents de 0.

Si G n'est pas simple, il existe un sous-groupe distingué H différent de G et de {1} et le quotient G/H est un groupe non résoluble d'ordre plus petit que celui de G, ce qui est impossible par hypothèse.

Aucune des deux valeurs m ou n ne peut être égale à 0. En effet, G serait un p-groupe et tous les p-groupes sont résolubles. De même, le groupe ne peut être abélien, car tout groupe abélien est nilpotent donc résoluble.

• Il existe un entier strictement positif d et un élément g de G tel le cardinal de la classe de conjugaison de g est égal à q^d.

Les théorèmes de Sylow montrent que G contient un p-groupe maximal, c'est à dire un sous-groupe S d'ordre pⁿ. Soit g un élément du centre de S, différent de 1. Un tel élément existe d'après les propriétés des p-groupes (cf p-groupe).

Le stabilisateur Stab_g de g contient S et le cardinal de la classe de conjugaison de g est égal au nombre de classe du quotient G/Stab_g (cf formule de Burnside). Comme le stabilisateur de g contient S son ordre est un multiple de pⁿ. Le cardinal de G/Stab_g est donc une puissance de q.

Le centre de G est réduit à l'élément neutre car G est simple, g qui est différent de 1 est élément d'une classe de conjugaison non réduite à un singleton, ce qui termine la démonstration.

• Il existe une représentation (V, ρ) irréductible de degré premier avec q dans un espace vectoriel complexe tel que son caractère χ_ρ possède une valeur non nulle en g dans l'anneau des entiers algébriques du centre de l'algèbre du groupe.

Soit (χ_i) la famille des caractères irréductibles de G. Ici χ₁ désigne le caractère trivial. Les caractères irréductibles forment une base orthonormale du centre de l'algèbre de G. On en déduit que les vecteurs colonnes (χ_i( x)), où x parcourent les classes de conjugaison de G, forment aussi une base orthonormale. Ceci montre que les deux vecteurs de C^h composés des différentes valeurs des caractères irréductibles au point 1 et au point g sont orthogonaux :

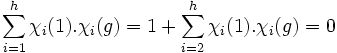
Et il existe des représentations irréductibles ayant un caractère non nul en g.

Terminons le raisonnement par l'absurde et supposons que tout caractère irréductible ayant une valeur non nul en g soit de degré un multiple de d, notons α_i l'entier tel que α_i.d soit le degré de la représentation de caractère χ_i. Si h désigne le nombre de classes de conjugaison de G et donc le nombre de caractères irréductibles, on obtient l'égalité suivante :

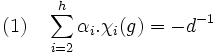
Or χ_i(g) est un entier algébrique car il est somme de racines de l'unité. Le terme de gauche est une combinaison linéaire à coefficients dans Z d'entiers algébriques et donc est un entier algébrique, or le terme de gauche n'est pas un entier algébrique. Cette contradiction démontre la fin de la proposition.

• La valeur q^d.χ_ρ(g)/χ_ρ(1) est un entier algébrique.

Soit g₁ l'élément de l'algèbre du groupe G sur les nombres complexes égal à la somme des conjugués de g. Alors g₁ est un entier algébrique du centre de l'algèbre du groupe (cf paragraphe Entier algébrique de l'article Algèbre d'un groupe fini).

L'application ρ est un morphisme d'algèbre de C[G], donc ρ(g₁) est donc aussi un entier algébrique. Or, si Id désigne l'identité de C[G] et c_g la classe de conjugaison de g, on a l'égalité :

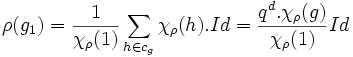
Car le cardinal de la classe de conjugaison de g est égal à q^d. Le fait que ρ(g₁) soit un entier algébrique démontre la proposition.

• La valeur χ_ρ(g)/χ_ρ(1) est un entier algébrique.

En effet, q est premier avec χ_ρ(1), l'identité de Bézout montre alors l'existence de deux entiers a et b tel que :

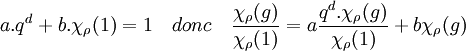
La valeur recherchée est donc combinaison linéaire à coefficients entiers d'entiers algébriques, ce qui démontre la proposition.

• Le module de χ_ρ(g) est égal au degré de la représentation ρ.

Notons ζ le ratio χ_ρ(g)/χ_ρ(1). Cette valeur est un entier algébrique non nul. Elle admet donc un polynôme minimal M[X] à coefficients dans les entiers relatifs. Le polynôme M[X] n'admet que des racines différentes de zéro, donc la norme N(ζ) de ζ est non nulle. Elle est égale, au signe près, au coefficient constant de M[X], et donc est un entier relatif non nul.

De plus, ζ est la somme de χ_ρ(1) racines de l'unité car χ_ρ(1) est égal au degré de la représentation ρ. En conséquence le module de χ_ρ(g) est inférieur ou égal au degré de la représentation. L'application qui à un nombre complexe associe son module est un automorphisme du corps de décomposition de ζ sur Q, l'ensemble des nombres rationnels, en conséquence, toute racine du polynôme M[X] possède un module inférieur ou égal à un et N(ζ) est un entier relatif non nul de module inférieur ou égal à un. N(ζ) est donc, en valeur absolue égal à un.

Toutes les racines de M[X] ont un module inférieur ou égal à un et leur produit est de module égal à un. Ceci démontre que le module d'une racine de M[X] et en particulier celui de ζ est égal à un.

• L'ensemble des éléments de G ayant pour image par χ_ρ un nombre complexe de module égal au degré de la représentation ρ est un sous-groupe normal H.

H contient l'élément neutre, il est donc non vide. Soit h un élément de H, l'égalité entre le module de χ_ρ(h) et celui de χ_ρ(1) signifie que toutes les valeurs propres de χ_ρ(h) sont égales, et donc que χ_ρ(h) est une homothétie de rapport une racine de l'unité. H est donc l'image réciproque par ρ du groupe des homothéties, c'est donc un sous-groupe normal.

• Conclusion

H est un sous-groupe normal non réduit à l'élément neutre car il contient g. Le sous-groupe H est donc égal à G car G est simple. Le noyau de ρ est aussi un sous-groupe-normal et, comme la représentation ρ n'est pas triviale, ce noyau est différent de G, il est donc égal à l'élément neutre.

G est donc isomorphe à H/Ker ρ, or le paragraphe précédent montre que H/Ker ρ, est un groupe abélien. G est donc un groupe abélien, ce qui est une contradiction avec la première proposition.

Cette contradiction démontre le théorème.