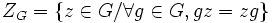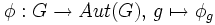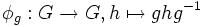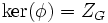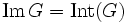Centre D'un Groupe

Centre d'un groupe

En théorie des groupes, on appelle centre d'un groupe $G$ l'ensemble des éléments qui commutent avec tous les autres.

Sommaire

1 Définition
2 Propriétés
3 Exemple
4 Application
5 Voir aussi

Définition

Soit $(G, * )$ un groupe, noté multiplicativement, de neutre $e$ .

$Z_G = \left\{ z \in G / \forall g \in G, g z = z g \right\}$

$Z G$ est un sous-groupe de $G$ .

Propriétés

On montre que $Z G$ est un sous-groupe distingué, abélien.

Exemple

Le centre d'un groupe abélien $G$ est le groupe $G$ entier, c'est-à-dire:

$Z_G = G \,$

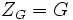
Application

On considère l'automorphisme intérieur :

$\phi : G \rightarrow Aut(G), \, g \mapsto \phi_g \,$

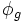où $\phi_g \,$ est l'automorphisme défini par:

$\phi _g : G \rightarrow G, h \mapsto g h g^{-1} \,$

On a alors:

$\ker (\phi)=Z_G \,$

$\mbox{Im} \, G= \mbox{Int}(G)$

Le sous-groupe $Int(G)$ est appelé groupe des automorphismes intérieurs de G.

On peut en déduire, d'après les théorèmes d'isomorphisme :

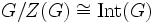$G/Z(G) \cong \mbox{Int}(G) \,$ .

Voir aussi

Centre (algèbre)

Portail des mathématiques

Ce document provient de « Centre d%27un groupe ».

Catégorie : Théorie des groupes

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Centre D'un Groupe de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Centre d'un groupe — En théorie des groupes, on appelle centre d un groupe G l ensemble des éléments qui commutent avec tous les autres. Sommaire 1 Définition 2 Propriétés 3 Exemples 4 Application … Wikipédia en Français
Centre France — Le groupe Centre France est un groupe français indépendant spécialisé dans la presse locale et le multi cross media dans le grand centre de la France. Son siège est à basé Clermont Ferrand, 45 rue du Clos Four. Centre France se distingue par une… … Wikipédia en Français
Centre national des indépendants et paysans — Présentation Président Gilles Bourdouleix Fondation 6 janvier 1949 Siège … Wikipédia en Français
Groupe D'armées Centre — Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le maréchal von Bock, fort… … Wikipédia en Français
Groupe d'Armée Centre — Groupe d armées Centre Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le… … Wikipédia en Français
Groupe d'Armée centre — Groupe d armées Centre Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le… … Wikipédia en Français
Groupe d'Armée du Centre — Groupe d armées Centre Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le… … Wikipédia en Français
Groupe d'armees Centre — Groupe d armées Centre Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le… … Wikipédia en Français
Groupe d'armée centre — Groupe d armées Centre Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le… … Wikipédia en Français
Groupe d'armées centre — Le groupe d armées Centre (allemand : Heeresgruppe Mitte) fut un groupe d armées de l Allemagne nazie créé le 22 juin 1941, lorsque le groupe d armées B fut renommé en groupe d armées Centre. Dirigé par le maréchal von Bock, fort… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Centre D'un Groupe