Sous-espaces supplémentaires

Sous-espaces supplémentaires

Sous-espace supplémentaire

En mathématiques, un sous-espace supplémentaire est un sous-espace vectoriel défini par rapport à un autre sous-espace qui, de manière intuitive (ne pas confondre avec la notion de complémentaire), sépare l'espace en deux parties d'intersection égale au vecteur nul, et de telle sorte que tout vecteur soit la somme d'un vecteur membre du sous-espace vectoriel et d'un élément de son supplémentaire. Les deux vecteurs formant la somme sont obtenus par des projecteurs. Le sous-espace et son supplémentaire sont dit en somme directe.

Pour comprendre de manière intuitive ce qu'est un sous-espace supplémentaire, posons E un espace vectoriel de dimension n, qui est engendré par une base B comportant donc n vecteurs et E1 un sous-espace vectoriel de E de dimension n1 et qui admet une base B1 comportant donc n1 vecteurs. Soit un sous-espace supplémentaire E2 de E1 dans E. E2 est un espace vectoriel de dimension n2 = n - n1 engendré par une base B2 comportant n2 vecteurs tels que la famille des vecteurs de B1 et de B2 soit libre (et soit donc une base de E). En fait, si on a une base de E1, on peut trouver une base d'un E2 en complétant la base de E1 pour obtenir une base de E, cette base de E2 étant composée des vecteurs que l'on a ajouté à la base de E1 pour obtenir une base de E.

Tout sous-espace vectoriel admet un supplémentaire, cependant dans le cas où la dimension n'est pas finie, alors la démonstration utilise le lemme de Zorn, et donc indirectement, l'axiome du choix.

Définition

Dans la suite de l'article E désigne un espace vectoriel, x désigne un vecteur quelconque de E et E1 et E2 deux sous-espaces vectoriels.

La définition d'un sous-espace supplémentaire est donnée par l'équivalence des quatre propositions suivantes:

  • E2 est un sous-espace supplémentaire de E1.
  • E1 et E2 ont une intersection réduite au vecteur nul et tout vecteur s'écrit comme la somme d'un vecteur de E1 et E2.
  • Tout vecteur x s'écrit de manière unique comme la somme d'un vecteur de E1 et d'un vecteur de E2.
  • Il existe deux projecteurs P1 et P2 tel que leur somme soit égal à l'identité et l'image de P1 (respectivement P2) soit égal à E1 (respectivement E2)

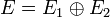Les deux sous-espaces sont alors dit en somme directe. On note E = E_1 \oplus E_2.

Démonstration
  • La deuxième proposition est équivalente à la troisième

Dire qu'il existe une manière unique d'écrire un vecteur comme somme de deux vecteurs de E1 et E2 signifie que tout vecteur de l'intersection des deux sous-espaces s'écrit comme la somme de deux vecteurs nulles.

  • La troisième proposition implique la quatrième proposition

Supposons la troisième proposition vraie. Soit x = x1 + x2 la décomposition de la troisième proposition. Définissons P1 (respectivement P2) comme l'endomorphisme qui à x associe x1 (respectivement x2).

Alors P1 (respectivement P2) sont linéaires, en effet si λ est un scalaire et y un vecteur ayant pour décomposition y = y1 + y2, alors:

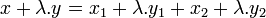
x+\lambda .y=x_1+\lambda .y_1+x_2+\lambda .y_2\;

est l'unique décomposition du vecteur x + λy. L'unicité de la décomposition montre les deux égalités suivantes et donc la linéarité de P1 et P2.

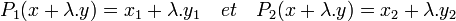
P_1(x+\lambda .y)=x_1+\lambda .y_1\quad et\quad P_2(x+\lambda .y)=x_2+\lambda .y_2\;

Les trois égalités suivantes montrent que P1 et P2 sont des projecteurs:

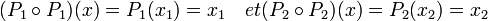
(P_1\circ P_1)(x)=P_1(x_1)=x_1\quad et (P_2\circ P_2)(x)=P_2(x_2)=x_2\;

Ces égalités montrent de plus que P1 (respectivement P2) a bien pour image E1 (respectivement E2), que la restruction de P1 (respectivement P2) sur leurs images est bien l'identité et que leur noyau est E2 (respectivement E1). L'égalité suivante montre que leur somme est égale à l'identité:

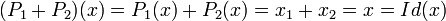
(P_1+P_2)(x)=P_1(x)+P_2(x)=x_1+x_2=x=Id(x)\;
  • La quatrième proposition implique la troisième proposition

L'égalité suivante montre l'existence d'une décomposition de x comme somme d'un vecteur de E1 et d'un vecteur de E2.

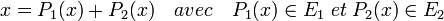
x=P_1(x)+P_2(x)\quad avec\quad P_1(x)\in E_1\; et\; P_2(x)\in E_2\;

Soit alors une décomposition x = x1 + x2 du vecteur comme somme d'un vecteur de E1 et d'un vecteur de E2. Les égalités suivantes montre l'unicité de x1 et x2.

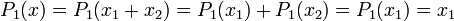
P_1(x)=P_1(x_1+x_2)=P_1(x_1)+P_1(x_2)=P_1(x_1)=x_1\;
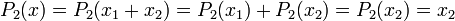
P_2(x)=P_2(x_1+x_2)=P_2(x_1)+P_2(x_2)=P_2(x_2)=x_2\;

Propriétés

  • Tout sous-espace vectoriel E1 admet un supplémentaire E2.
  • Dans le cas où E est de dimension finie, alors la dimension de E2 est égale à la codimension de E1.
  • Si E2 est un supplémentaire de E1, Alors E est isomorphe au produit cartésien E1xE2.
Démonstration
  • Tout sous-espace vectoriel E1 admet un supplémentaire E2.

C'est une conséquence directe du théorème de la base incomplète. Soit une base de E1, elle forme une famille libre de E, elle peut donc être complétée pour former une base de E. L'espace engendré par les vecteurs complétant la base est un supplémentaire.

  • Dans le cas ou E est de dimension finie, alors la dimension de E2 est égale à la codimension de E1.

La démonstration est donnée dans l'article Codimension.

Considérons l'application qui de E1xE2 dans E qui à (x1,x2) associe x1+x2. Cette application est linéaire, son noyau est, par construction réduit au vecteur nul et son image est E. Il existe donc un isomorphisme entre les deux structures.

Liens internes

Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs Colinéarité • Indépendance linéaire • Famille libre • Rang • Famille génératrice • Base • Théorème de la base incomplète Mathématiques
Sous-espace Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension d'un espace vectoriel • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Endomorphisme nilpotent
En dimension finie Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford
Enrichissements de structure Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Sous-espace suppl%C3%A9mentaire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sous-espaces supplémentaires de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Sous-espace supplémentaire — En mathématiques, plus précisément en algèbre linéaire, deux sous espaces vectoriels d un même espace vectoriel sont supplémentaires dans cet espace si tout vecteur de l espace se décompose de façon unique en une somme d un vecteur de chacun des… …   Wikipédia en Français

  • Espaces vectoriels — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… …   Wikipédia en Français

  • Sous-espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Espaces euclidiens — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique …   Wikipédia en Français

  • Sous-espace stable — En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F. La recherche de sous espaces stables est étroitement liée à la théorie de la réduction des endomorphismes.… …   Wikipédia en Français

  • Influenzavirus A sous-type H5N1 — Virus A (H5N1) …   Wikipédia en Français

  • Influenzavirus A Sous-Type H5N1 — Virus A (H5N1) …   Wikipédia en Français

  • Influenzavirus a sous-type h5n1 — Virus A (H5N1) …   Wikipédia en Français

  • Dimensions supplémentaires — Les dimensions enroulées, ou dimensions supplémentaires sont les fondements de la théorie de Kaluza Klein mais apparaissent également dans des modèles plus généraux de compactification utilisés en cosmologie branaire ou en théorie des supercordes …   Wikipédia en Français

  • Dimensions Supplémentaires — Les dimensions enroulées, ou dimensions supplémentaires sont les fondements de la théorie de Kaluza Klein mais apparaissent également dans des modèles plus généraux de compactification utilisés en cosmologie branaire ou en théorie des supercordes …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”