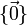Sous-espaces vectoriels triviaux
- Sous-espaces vectoriels triviaux
-
Sous-groupes triviaux
Soit G un groupe, on appelle sous-groupes triviaux de G :
- Le groupe constitué de l'élément neutre
- Le groupe G lui-même
Sous groupe vectoriel triviaux
Soit E un espace vectoriel.
Les deux sous-espaces vectoriels :
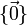
- E
sont qualifiés de triviaux.
Ce sont aussi les sous-groupes triviaux de E pour l'addition
Voir aussi
Catégorie : Groupe remarquable
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Sous-espaces vectoriels triviaux de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Sous-espace vectoriel — En algèbre linéaire, étant donné un espace vectoriel E sur un corps K, un sous espace vectoriel de E est une partie non vide F de E stable par combinaisons linéaires. Autrement dit, cette partie doit vérifier : La somme vectorielle de deux… … Wikipédia en Français
Sous-groupes triviaux — Soit G un groupe, on appelle sous groupes triviaux de G : Le groupe constitué de l élément neutre Le groupe G lui même Sous groupe vectoriel triviaux Soit E un espace vectoriel. Les deux sous espaces vectoriels : E sont qualifiés de… … Wikipédia en Français
Algebre universelle — Algèbre universelle L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de… … Wikipédia en Français
Algèbre Universelle — L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces vectoriels, etc. Elle permet de définir de manière… … Wikipédia en Français
Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces … Wikipédia en Français
ALGÈBRE — L’algèbre au sens moderne, à savoir l’étude des structures algébriques indépendamment de leurs réalisations concrètes, ne s’est dégagée que très progressivement au cours du XIXe siècle, en liaison avec le mouvement général d’axiomatisation de… … Encyclopédie Universelle
Idéal — Pour les articles homonymes, voir Idéal (homonymie). En mathématiques, et plus particulièrement en algèbre, un idéal est un sous ensemble remarquable d un anneau. Par certains égards, les idéaux s apparentent aux sous espaces vectoriels ce sont… … Wikipédia en Français
Anneau Noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une addition et d une… … Wikipédia en Français
Anneau noetherien — Anneau noethérien Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelé anneau noethérien. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble munis d une… … Wikipédia en Français
Anneau noethérien — Emmy Noether formalise les propriétés d une famille particulière d anneaux maintenant appelés anneaux noethériens. En mathématique, un anneau noethérien est un cas particulier d anneau, c est à dire d un ensemble muni d une addition et d une… … Wikipédia en Français