- Dimensions supplémentaires
-
Les dimensions enroulées, ou dimensions supplémentaires sont les fondements de la théorie de Kaluza-Klein mais apparaissent également dans des modèles plus généraux de compactification utilisés en cosmologie branaire ou en théorie des supercordes. L'idée générale est la suivante : notre univers ne contiendrait pas seulement les quatre dimensions spatio-temporelles que nous lui connaissons, appelées dimensions étendues, mais il contiendrait aussi des dimensions supplémentaires, minuscules, car enroulées sur elles-mêmes.
Sommaire
Apparence
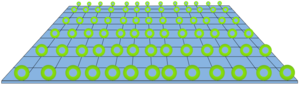
Des dimensions enroulées en cercles, constituant un modèle d'univers. Ce modèle ne fait apparaitre qu'une seule dimension supplémentaire.
Des dimensions enroulées en tores, constituant un autre modèle d'univers. Il fait apparaitre 3 dimensions supplémentaires.
Des dimensions enroulées en espaces de Calabi-Yau, constituant le modèle d'univers le plus efficace en théorie des cordes, puisqu'il apporte 6 dimensions supplémentaires.Dans les modèles les plus simples comme la théorie de Kaluza-Klein, les dimensions peuvent être enroulées en sphères (pleines ou creuses), en tores ou en cercles de taille mesurée avec une échelle naturelle donnée par la longueur de Planck : LPlanck ~ 10-33 cm[2] .
Dans des modèles plus évolués, tels ceux apparaissant dans la théorie des supercordes, l'espace de compactification peut avoir une structure géométrique plus compliquée comme celle d'un espace de Calabi-Yau par exemple. Notons que dans le cadre de la cosmologie branaire il est également possible de considérer des modèles dans lesquels les dimensions supplémentaires sont bien plus grandes que la longueur de Planck et peuvent atteindre des dimensions d'une taille de l'ordre du millimètre sans entrer en contradiction avec les limites expérimentales actuelles concernant la loi de la gravitation. Ces modèles branaires sont eux-mêmes inspirés de modèles phénoménologiques apparaissant dans la théorie des supercordes, et pour lesquels la géométrie de l'espace total n'est pas un simple produit entre la géométrie visible et la géométrie des dimensions supplémentaires[3], mais possède une structure plus complexe mélangeant les deux. On appelle ce type de construction une compactification tordue (twisted compactification en anglais).
Apparition de dimensions enroulées
Ces dimensions sont nées durant l'ère de Planck. C'est la théorie des cordes qui explique comment ces dimensions sont restées enroulées. Durant l'ère de Planck, toutes les dimensions étaient enroulées. Elles étaient prisonnières des cordes. Certaines dimensions ont réussi à s'en libérer alors que les autres sont restées enroulées. Les dimensions apparentes (celles que l'on perçoit) ont donc la taille de l'univers.
Par contre, d'autres dimensions peuvent être sous-jacentes à la réduction dimensionnelle.Position de ces dimensions
Elles se situeraient à chaque point de l'espace-temps[4]. À chaque mouvement que nous faisons, l'objet de ces déplacements (une voiture, le bras, n'importe quoi en mouvement) revient au même endroit dans les dimensions enroulées. Cela est logique vu qu'il nous est impossible d'évoluer dans ces dimensions microscopiques.
Applications du modèle
- Les équations de Theodor Kaluza, qui avaient pour but l'unification de la force gravitationnelle et de la force électromagnétique, ont démontré que cela était possible dans un univers à cinq dimensions spatio-temporelles.
- La théorie des cordes a démontré que l'unification des équations de la relativité générale et celles de la mécanique quantique était possible dans un univers à dix dimensions d'espace-temps.
- Le physicien Edward Witten a démontré avec la théorie M que l'unification des cinq théories des cordes était possible dans un univers à onze dimensions spatio-temporelles.
Univers en Tore bidimensionnel
Un tel univers présente des mirages topologiques marqués par une répétition orthogonale du contenu de l'univers. C'est donc un univers multiconnexe.Un photon qui dépasse une frontière se retrouve du côté opposé. On observe ainsi le motif de l'univers répété dans les deux directions. En topologie, un tore bidimensionnel est un objet de taille finie mais qui n'a pas de bord car il se boucle sur lui-même. À chaque fois que l'on franchirait un bord, on se retrouve de l'autre côté du tore. Si on franchit le bord de droite, on se retrouvera sur le bord de gauche, si on dépasse le bord du haut, on se retrouve sur le bord du bas, et vice versa. Le haut et le bas, la gauche et la droite sont identifiés.
Un tore — tel qu'on peut s'en représenter visuellement — paraît courbe car on l'imagine usuellement avec une forme de pneu. En réalité cette courbure n'est qu'apparente, dans notre espace à trois dimensions, on appelle ceci la courbure externe. D'un point de vue interne un tore est en réalité tout à fait plat, euclidien, et sa courbure intrinsèque est nulle.
Univers fractal : En cosmologie, le modèle de l'Univers fractal désigne un modèle cosmologique dont la densité de matière est presque nulle et suit une répartition fractale.
Quatrième dimension En géométrie
Un point translaté donne un segment, un segment translaté donne un carré, un carré translaté donne un cube, un cube translaté donne un tesseract etc. En géométrie euclidienne Les concepts de plans et d'espaces euclidiens peuvent être encore élargis à d'autres dimensions au dessus. On passe d'un univers à 3 dimensions (espace) à un univers à 4 dimensions de la même façon qu'on passe d'un univers à 2 dimensions (plan) à un univers à 3 dimensions (espace) et de la même façon qu'on passe d'un univers à 1 dimension (droite) à un univers à 2 dimensions (plan)... Le repère orthonormé d'un univers à N dimensions est alors formé de N axes gradués, tous perpendiculaires entre eux les uns les autres en un même point appelé origine. Par exemple, un tesseract est un objet à quatre dimensions spatiales : son intersection avec un espace peut être un cube de la même façon que l'intersection d'un cube avec un plan peut donner un carré.
En géométrie non euclidienne Les géométries à N dimensions et les géométries non-euclidiennes sont deux branches séparées de la géométrie. Une confusion s'est établie dans la littérature populaire à propos de ces deux géométries. Parce que la géométrie euclidienne était à trois dimensions, on en concluait que les géométries non-euclidiennes comportaient nécessairement des dimensions supérieures.
Notion de 4e dimension chez Poincaré "L'espace moteur aurait autant de dimensions que nous avons de muscles" : cette affirmation de Poincaré dans La Science et l'Hypothèse est la marque de distinction la plus claire entre les deux sortes d'espace qu'il envisage : l'espace géométrique et l'espace représentatif.
Voir aussi
Notes
- Dans le cas de sphères creuses, il n'est possible de considérer que la surface de la sphère, qui est bidimensionnelle. Un tel modèle ne génère donc pas 3, mais 2 dimensions supplémentaires.
- Ces dimensions sont extrêmement petites : ainsi, à la même échelle, une de ces dimensions aurait la taille d'un arbre si un atome d'hydrogène avait la taille du système solaire !
- Ce qui est le cas dans la théorie de Kaluza-Klein.
- Pour des soucis de clarté, les dimensions enroulées des illustrations ne sont pas placées en chaque point.
Liens internes
Liens externes
- (en)[PDF] G.F. Giudice, J.D.Wells, Extra dimensions, disponible sur la page [1] et inclus dans la Review of Particle Physics publiée par le Particle Data Group (édition 2006).
Wikimedia Foundation. 2010.
