Variete algebrique

Variete algebrique: Variété algébrique

Pour les articles homonymes, voir variété.

Une variété algébrique est, de manière informelle, l'ensemble des racines communes d'un ensemble de polynômes en plusieurs indéterminées. La géométrie algébrique est la théorie qui étudie les variétés algébriques, et plus généralement les schémas.

Il y a deux points de vue (essentiellement équivalents) sur les variétés algébriques: elles peuvent être définies comme des schémas de type fini sur un corps (langage de Grothendieck), ou bien comme la restriction d'un tel schéma au sous-ensemble des points fermés. On utilisera ici le deuxième point de vue.

Dans un premier temps, on présente les variétés algébriques (quasi-projectives) sous l'angle concret des ensembles algébriques. Ensuite on donne la définition générale avec les espaces topologiques annelés.

Sommaire

1 Ensembles algébriques

1.1 Les ensemble algébriques affines

1.2 Les ensembles algébriques projectifs

1.3 Topologie de Zariski

1.4 Morphismes de variétés

2 Variétés algébriques

2.1 Variétés affines

2.1.1 Spectre maximal

2.1.2 Faisceaux des fonctions régulières

2.2 Définition des variétés algébriques et des morphismes

2.3 Propriétés de base

2.4 Aspect différentiel

2.4.1 Espace tangent

2.4.2 La suite

2.5 Aspect arithmétique

Ensembles algébriques

Les ensembles algébriques sont, grosso modo, les points d'une variété algébrique.

Les ensemble algébriques affines

C'est le prototype des ensembles algébriques.

Cadre. Dans cette section k désignera un corps algébriquement clos (par exemple 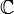$\mathbb{C}$ ), n un entier supérieur ou égal à un. On considère l'espace affine de dimension n sur k, c’est-à-dire l'ensemble kⁿ.

Définition. Soit S une partie de l'anneau des polynômes $k[X_1,\ldots,X_n]$ , on appelle ensemble algébrique associé à S et on note Z(S) le sous-ensemble de kⁿ:

$Z(S)=\{(x_1,\ldots,x_n)\in \mathbb{A}_k^n, \forall f\in S,\ f(x_1,\ldots,x_n)=0\}$

C’est-à-dire le lieu d'annulation commun à tous les éléments de S.

Remarque. Si I est l'idéal de $k[X_1,\ldots,X_n]$ engendré par S, alors Z(I)=Z(S). Le théorème des zéros de Hilbert établit une correspondance bijective entre les ensembles algébriques de kⁿ et les idéaux radiciels de $k[X_1,\ldots,X_n]$ . Cette correspondance envoie un ensemble algébrique Z sur l'idéal des polynômes s'annulant en tous les points de Z. Les points de Z(I) correspondent aux idéaux maximaux de $k[X_1,\ldots,X_n]/I$ , et les ensembles algébriques correspondant aux idéaux premiers sont dits irréductibles.

Exemples.

Dans le plan affine $k 2$ , le lieu d'annulation d'un polynôme à deux variables est un ensemble algébrique affine appelé courbe plane et le degré du polynôme est appelé degré de la courbe. Les droites sont les ensembles algébriques de degré 1, les coniques ceux de degré 2, les cubiques ceux de degré 3 et ainsi de suite.

Dans l'espace affine $k 3$ le lieu d'annulation d'un polynôme à trois variables est un ensemble algébrique affine qui est une surface algébrique . Tout comme pour les courbes on définit le degré d'une surface, les plans sont de degré 1, les quadriques de degré 2 etc.

Dans un espace affine, un ensemble fini de points est un ensemble algébrique affine.

Les ensembles algébriques projectifs

La géométrie algébrique projective est un cadre plus confortable. La projectivité est un analogue de la compacité topologique. Le théorème de Bezout n'est vrai que pour des variétés projectives.

Cadre. Dans cette partie $\mathbb{P}_k^n$ désigne l'espace projectif de dimension n sur k, c'est-à-dire l'ensemble kⁿ⁺¹−{0}/~, où ~ est la relation d'équivalence identifiant deux points x et y si et seulement si x et y sont sur la même droite passant par l'origine. L'espace projectif de dimension n s'identifie donc à l'ensemble des droites vectorielles d'un k-espace vectoriel de dimension n+1.

Définition. Soit S un ensemble de polynômes homogènes de l'anneau $k[X_0,\ldots,X_n]$ . On appelle ensemble algébrique (projectif) associé à S et on note Z_+(S) le sous-ensemble de $\mathbb{P}_k^n$ :

$Z_+(S)=\{(x_0:\ldots:x_n)\in \mathbb{P}_k^n, \forall f \in S,\ f(x_0,\ldots,x_n)=0\}$

$(x_0 : \ldots : x_n)$ sont les coordonnées homogènes d'un point de $\mathbb{P}_k^n$ . Remarquons que l'annulation du polynôme f en un point de $k n + 1 - 0$ ne dépend que de la classe de ce point modulo la relation ~. L'ensemble Z_+(S) est donc bien défini. L'indice + sert à distinguer les zéros homogènes des zéros affines.

Exemple Soit F un polynôme homogène à deux variables, non-nul, de degré d. L'ensemble algébrique projectif Z_+(F) du plan projectif $\mathbb{P}_k^2$ est appelé une courbe projective plane, de degré d.

Remarque. Si I est l'idéal homogène de $k[X_0,\ldots,X_n]$ engendré par S alors Z(I)=Z(S). Ensuite, tout comme dans le cas des ensembles algébriques affines il existe un théorème des zéros de Hilbert projectif qui établit une correspondance bijective entre les ensembles algébriques projectives dans $\mathbb{P}_k^n$ et les idéaux homogènes radiciels distincts de $(X_0,\ldots,X_n)$ (idéal engendré par $X_0,\ldots,X_n$ . Un point de l'espace projectif correspond à un idéal premier homogène, maximal parmi ceux différent de $(X_0,\ldots,X_n)$ . À un point de coordonnées homogène $(x_0 : \ldots : x_n)$ , on lui associe l'idéal engendré par les $x i X j - x j X i$ , pour i et j variant entre 0 et n.

Topologie de Zariski

L'espace affine kⁿ (resp. projectif $\mathbb{P}_k^n$ ) est muni de la topologie dite de Zariski. Les fermés pour cette topologie sont les ensembles algébriques (resp. ensembles algébriques projectifs). La topologie de Zariski sur un ensemble algébrique (resp. ensemble algébrique projectif) est induite par celle de l'espace affine (resp. projectif) qui le contient.

Un sous-ensemble ouvert d'un ensemble algébrique affine (resp. projectif) est appelé quasi-affine (resp. quasi-projectif).

L'espace affine kⁿ est quasi-projectif car il s'identifie à l'ouvert $\mathbb{P}_k^n - Z_+(X_0)$ de $\mathbb{P}_k^n$ par l'application (x₁,...x_n) -> (1:x₁,...,x_n). On vérifie que cette application induit un homéomorphisme de l'espace affine sur son image. Il suit que tout ensemble algébrique quasi-affine est quasi-projectif.

Exemple: Les parties fermées de la droite affine k sont les parties finies et k lui-même.

La topologie de Zariski est apparemment assez pauvre (peu d'ouverts, deux points ne sont en général pas séparés par des voisinages ouverts disjoints), mais elle est suffisante pour beaucoup de propos.

Relations entre ensembles algébriques affines et ensembles algébriques projectifs : Un ensemble algébrique projectif Z est réunion finie d'ouverts (pour sa topologie de Zariski) qui sont des ensembles algébriques affines. En effet, Z est défini par l'annulation de polynômes homogènes à n variables. Notons $Z i$ l'ensemble des $(x_0 : ... : x_n)\in Z$ tels que $x i$ soit non-nul. Alors $Z_i=Z\setminus Z\cap Z_+(x_i)$ est ouvert dans $Z$ ; les $Z i$ recouvrent $Z$ ; il reste à voir que $Z i$ est un ensemble algébrique affine. Si $Z = Z + (S)$ , et si $S i$ est l'ensemble des polynômes $F (x 0,..., x i - 1,1, x i + 1,..., x n)$ quand les $F$ parcourent les polynômes homogènes dans $S$ , alors on voit facilement que $Z i$ est l'ensemble algébrique $Z (S i)$ dans $k n$ .

Morphismes de variétés

Variétés algébriques

Variétés affines

Spectre maximal

Soit k un corps. Une algèbre de type fini sur k est un quotien d'une algèbre des polynômes $k [x 1,..., x n]$ par un idéal. Soit A une telle algèbre. On note Spm A l'ensemble des idéaux maximaux de A. Pour tout idéal I de A, $V (I)$ désigne l'ensemble des idéaux maximaux de A contenant I. Par exemple $V (0) = S p m A$ et $V (A)$ est l'ensemble vide. On vérifie facilement que $V(I) \cup V(J)=V(IJ)$ et que $\cap_i V(I_i)=V(\sum_i I_i).$ Ainsi, les ensembles de la forme $V (I)$ définissent la topologie de Zariski sur Spec A dont ils sont les parties fermées. Un ouvert de la forme $Spec A \ V(fA)$ est noté $D (f)$ et est appelé un ouvert principal. Les ouverts principaux forment une base de topologie.

Faisceaux des fonctions régulières

Soit A une algèbre de type fini sur k. Notons $X = S p m A$ muni de la topologie de Zariski. Pour tout ouvert principal $D (f)$ de X, on pose $O X (D (f)) = A f$ la localisation de A par rapport à la partie multiplicative des puissances positives de $f$ . On montre alors qu'il existe un unique faisceau de k-algèbres $O X$ sur $X$ tel que

$O X (D (f)) = A f$

les germes $O X, x$ de $O X$ en un point $x$ correspondant à un idéal maximal M de A est isomorphe à la localisation $A M$ de A par rapport à l'idéal maximal M.

Ainsi le couple $(X, O X)$ est un espace localement annelé. Tout espace localement annelé en k-algèbres isomorphe à un tel espace est appelé une variété algébrique affine sur k. Les éléments de $O X (U)$ pour un ouvert $U$ de $X$ sont appelés les fonctions régulières sur $U$ .

Exemple L'algèbre $k [x 1,..., x n]$ définit une variété affine appelée l'espace affine de dimension n et noté $A^n_k$ . On peut montrer que tout ouvert $U$ de l'espace affine est principal: $U = D (f)$ pour un certain polynôme $f$ . L'ensemble $O (U)$ des fonctions régulières sur $U$ est alors l'ensemble des fractions rationnelles $g / f d$ où $g$ est un polynôme et où $d$ est un entier positif ou nul.

Intuition Supposons pour simplifier que $k$ est algébriquement clos. Soit 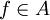$f\in A$ . Pour tout $x\in Spm A$ correspondant à un idéal maximal $M$ de $A$ , on note $f (x)$ l'image de $f$ dans le quotient $A / M = k$ . On définit ainsi une fonction $X \to k$ . D'où l'appellation "fonctions régulières" (par opposition aux "fonctions rationnelles" qui peuvent "prendre la valeur infinie"). Noter que la fonction associée à $f$ peut être identiquement sans que $f$ soit lui-même nul dans $A$ . En fait, en utilisant le théorème des zéros de Hilbert, on peut voir que la fonction associée à $f$ est identiquement nulle si et seulement si $f$ est nilpotent. Si $A = k [x 1,..., x n]$ , la fonction associée à $f$ n'est autre que la fonction polynomiale associée au polynôme $f$ .

Définition des variétés algébriques et des morphismes

On fixe un corps k.

Une variété algébrique sur k est un espace localement annelé (X, O_X) en k-algèbres qui admet un recouvrement fini par des ouverts affines $X i$ (c'est-à-dire que l'espace $(X_i, O_X|_{X_i})$ est une variété affine). On omet souvent $O X$ dans la notation d'une variété algébrique.

Un morphisme de variétés algébriques $f : X \to Y$ sur k est tout simplement un morphisme d'espaces localement annelés sur k. Comme tel, le morphism est composé d'une application continue $f : X \to Y$ et d'un morphisme de faisceaux de k-algèbres $f^{\#}$ $: O_Y \to f_*O_X$ . De même, on omettra souvent $f^{\#}$ dans les notations des variétés algébriques.

Propriétés de base

Fermés irréductibles, dimension, variétés réduites, intègres.

Morphismes: immersions, morphismes affines, morphismes propres, morphismes projectifs, morphismes finis.

Produit : définition, produits de variétés affines, produits de variétés projectives (Segre).

Aspect différentiel

Espace tangent

Soit $x$ un point d'une variété algébrique $X$ . Soit $m x$ l'idéal maximal de l'anneau local $O X, x$ de $X$ en $x$ . Rappelons que le corps $k (x) = O X, x / m x$ est le corps résiduel en $x$ . Il peut être vu comme la plus petite extension de k contenant les coordonnées de $x$ . Le quotient (de $O X, x$ -modules) $m_x/m_x^2$ (isomorphe à $m_x\otimes_{O_{X,x}} k(x)$ ) est un $k (x)$ -espace vectoriel de dimension finie (car $O X, x$ étant noethérien, $m x$ est un module de type fini). Le dual de cet espace vectoriel est appelé espace tangent de Zariski de $X$ en $x$ . On le note parfois $T X, x$ .

La construction des espaces tangents est fonctorielle: si $f : X\to Y$ est un morphisme de variétés algébriques sur k, alors f induit canoniquement une application linéaire $T_{X,x}\to T_{Y,y}\otimes_{k(y)} k(x)$ , où $y = f (x)$ . Cette application est l'application tangente de f en x, que l'on note parfois $T f, x$ .

Exemples

L'espace tangent de l'espace affine $A^n_k$ en un point rationnel s'identifie à $k n$ .

Supposons k algébriquement clos pour simplifier. Soit $X : = S p m (k [u, v] / (u 2 - v 3))$ . Alors l'espace tangent de $X$ au point $u = v = 0$ est un k-espace vectoriel de dimension 2. Il est de dimension 1 en tous les autres points.

Pour toute variété algébrique $X$ et pour tout point $x\in X$ , on a
$\dim \O_{X,x} \le \dim_{k(x)} T_{X,x}.$
La dimension de gauche étant la dimension de Krull de l'anneau local $O X, x$ , celle de droite étant la dimension vectorielle.

La suite

variétés algébriques lisses (non-singulières), critère jacobien, morphismes étales et structure locale de variétés lisses (revêtements étales d'espaces affines, comparaison avec les variétés différentielles ou complexes).

Aspect arithmétique

Points rationnels, extension de scalaires

Exemples, Conjecture de Mordell (=Théorème de Faltings) pour les courbes, théorème de Mordell-Weil pour les variétés abéliennes...

Portail des mathématiques

Ce document provient de « Vari%C3%A9t%C3%A9 alg%C3%A9brique ».

Catégorie : Géométrie algébrique

Contenu soumis à la licence CC-BY-SA. Source : Article Variete algebrique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Variété algébrique — Pour les articles homonymes, voir variété. Une variété algébrique est, de manière informelle, l ensemble des racines communes d un nombre fini de polynômes en plusieurs indéterminées. C est l objet d étude de la géométrie algébrique. Les schémas… … Wikipédia en Français
Variété algébrique affine — Ne doit pas être confondu avec les variétés affines (ou sous espaces affines) en géométrie affine En géométrie algébrique, une variété affine est un modèle local pour les variétés algébriques, c est à dire que celles ci sont obtenues par… … Wikipédia en Français
Variété algébrique non singulière — Une variété algébrique non singulière (ou lisse) est une variété dépourvue de point singulier. C est le cadre naturel de nombre de théorèmes fondamentaux en géométrie algébrique. Définition On dit qu une variété algébrique X est régulière lorsque … Wikipédia en Français
Variété algébrique projective — En géométrie algébrique, les variétés projectives forment une classe importante de variétés. Elles vérifient des propriétés de compacité et des propriétés de finitude. C est l objet central de la géométrie algébrique globale. Sur un corps… … Wikipédia en Français
Variete abelienne — Variété abélienne En mathématiques, une variété abélienne A est, grosso modo, un groupe algébrique projectif. La projectivité (l équivalent de compacité pour les variétés différentielles ou analytiques) donne une certaine rigidité à la strucutre … Wikipédia en Français
Variete — Variété Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 En biologie 2 En mathématiques 3 … Wikipédia en Français
Algebrique — Algébrique Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Variété abélienne — En mathématiques, et en particulier, en géométrie algébrique et en analyse complexe, une variété abélienne A est une variété algébrique projective qui est un groupe algébrique. La condition de « projectivité » est l équivalent de… … Wikipédia en Français
Variété (géométrie) — Pour les articles homonymes, voir Variété. Réalisation du ruban de Möbius à partir du collage d une bande de papier. Le « bord » n est que d un seul tenant. En math … Wikipédia en Français
Variété jacobienne — En géométrie algébrique, la jacobienne d une courbe C est une variété algébrique (en fait une variété abélienne) qui paramètrise les diviseurs de degré 0 sur C. C est un objet fondamental pour l étude des courbes, et c est aussi un exemple… … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts