- Loi du χ²
-
Loi du χ2 Densité de probabilité / Fonction de masse
Fonction de répartition
Paramètres  degrés de liberté
degrés de libertéSupport 
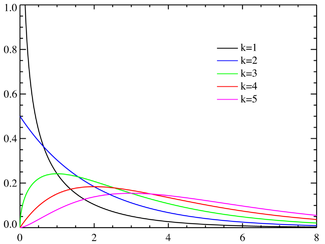
Densité de probabilité (fonction de masse) 
où Γ est la fonction gamma
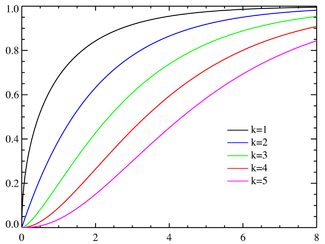
Fonction de répartition 
où γ est la fonction gamma incomplète
Espérance 
Médiane (centre) 
Mode  si
si 
Variance 
Asymétrie 
Kurtosis normalisé 
Entropie 
Fonction génératrice des moments  pour
pour 
Fonction caractéristique 
modifier 
La loi du χ2 (prononcer « khi-deux » ou « khi carré ») est une loi à densité de probabilité. Cette loi est caractérisée par un paramètre dit degrés de liberté à valeur dans l'ensemble des entiers naturels (non nuls).
Soient
 k variables aléatoires indépendantes de même loi normale centrée et réduite, alors par définition la variable
k variables aléatoires indépendantes de même loi normale centrée et réduite, alors par définition la variable  , telle que
, telle que
suit une loi du χ² à k degrés de liberté.
Soit
 une variable aléatoire suivant une loi du χ² à
une variable aléatoire suivant une loi du χ² à  degrés de liberté, on notera
degrés de liberté, on notera  la loi de
la loi de  .
.Alors la densité de
 notée
notée  sera :
sera : pour tout t positif
pour tout t positifoù Γ est la fonction gamma.
L'espérance mathématique de X vaut k et sa variance vaut 2k.
Sommaire
Approximation
Conformément au théorème de la limite centrale lorsque k est « grand » (k > 100), la loi d'une variable de χ², somme de variables aléatoires indépendantes, peut être approchée par une loi normale d'espérance k et de variance 2k.
D'autres fonctions en χ² peuvent converger plus rapidement vers la loi normale, notamment en ayant X~χ²(k) et k>30:
 tend approximativement vers la loi normale centrée réduite (Ronald Aylmer Fisher).
tend approximativement vers la loi normale centrée réduite (Ronald Aylmer Fisher).![\scriptstyle\sqrt[3]{X/k}](d/6bd5442dd615e41c37b9f37030637ce1.png) tend approximativement vers la loi normale de moyenne
tend approximativement vers la loi normale de moyenne  et de variance
et de variance  (Wilson et Hilferty, 1931).
(Wilson et Hilferty, 1931).
Utilisation
La principale utilisation de cette loi consiste à apprécier l'adéquation d'une loi de probabilité à une distribution empirique en utilisant le test du χ² basé sur la loi multinomiale. Plus généralement elle s'applique dans le test d'hypothèses à certains seuils (indépendance notamment).
Lien avec les méthodes bayésiennes
Dans son ouvrage Décisions rationnelles dans l'incertain (1974), qui constitue une somme des techniques bayésiennes dont la grande émergence se fait à cette époque, le professeur Myron Tribus montre que le χ² constitue un exemple de passage à la limite du psi-test (test de plausibilité) bayésien lorsque le nombre de valeurs en présence devient grand - ce qui est la condition de travail des statistiques classiques, mais pas nécessairement des bayésiennes. Le raccord entre les deux disciplines, qui sont asymptotiquement convergentes, est ainsi complet.
L'ouvrage de référence de Jaynes en donne également une démonstration en page 287[1].
Voir aussi
Articles connexes
Notes et références
- Portail des probabilités et des statistiques
Wikimedia Foundation. 2010.
