Loi de Benford

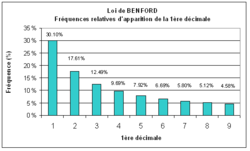
La loi de Benford, également appelée loi des nombres anormaux, énonce que dans une liste de données statistiques, le 1^er chiffre non nul le plus fréquent est 1, pour près du tiers des observations. Puis le 2 est lui-même plus fréquent que 3… et la probabilité d'avoir un 9 comme premier chiffre significatif n'est que de 4,6 %.

De façon générale, la loi donne la valeur théorique f de la fréquence d'apparition du premier chiffre d'un nombre d d'un résultat de mesure exprimé dans une base b donnée au moyen d'une unité.

$f = \log_{b} \left(1 + \frac 1 d\right )$

Historique

Cette distribution a été observée une première fois en 1881 par l'astronome américain Simon Newcomb, dans un article de l'American Journal of Mathematics^[1], après qu'il se fut aperçu de l'usure (et donc de l'utilisation) préférentielle des premières pages des tables de logarithmes (alors compilées dans des ouvrages). Cet article de Newcomb passe complètement inaperçu pendant cinquante-sept ans. Frank Benford, aux alentours de 1938, remarqua à son tour cette usure inégale, crut être le premier à formuler cette loi qui porte indûment son nom aujourd'hui, et arriva aux même résultats après avoir répertorié des dizaines de milliers de données (longueurs de fleuves, cours de la bourse, etc).

Applications

Détection de la fraude fiscale

La loi de Benford est utilisée aux États-Unis, ainsi que dans d'autres pays, dont la France, pour détecter des fraudes fiscales, suite aux idées exposées en 1972 par Hal Varian^[2]. Les premiers chiffres significatifs 5 et 6 prédominent nettement dans les données falsifiées : 40 % pour les 5 et plus de 20 % pour les 6. Pour proposer un modèle de prédiction d'indice boursier, il convient d'inclure un test de cohérence car la loi de Benford ne fait pas de distinction entre les nombres 20 et 200 000 : ces deux nombres ayant 2 et 0 comme chiffres significatifs^[3].

Données comptables

Dans une étude publiée en 2011, quatre économistes allemands, Bernhard Rauch, Max Göttsche, Gernot Brähler et Stefan Engel ont testé la loi de Benford sur les données comptables produites par les Etats membre de l'Union européenne. Ils montrent que la Grèce est le pays européen qui s'éloigne le plus des prédictions de la loi de Benford. La Belgique est le second pays qui dévie le plus par rapport à cette loi^[4]^,^[5].

Détection de la fraude électorale

Article détaillé : Fraude électorale.

La loi de Benford a aussi été utilisée pour mettre en évidence la fraude électorale. Trois politologues ont publié une étude montrant à partir de simulations que la mise en évidence de la fraude à partir d'un test d'adéquation à la loi de Benford était problématique et ne donnait pas de bons résultats sur les données simulées^[6].

Système décimal

En particulier, pour le système décimal (base 10), on a donc :

$f = \log_{10} \left(1 + \frac 1 d\right )$

Ce qui aboutit au tableau de résultats suivants :

Fréquences relatives d'apparition du 1^er chiffre (base 10) (%)
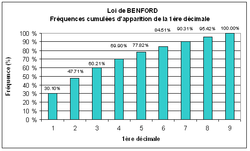
$d$	1	2	3	4	5	6	7	8	9
$f$	30,1	17,6	12,5	9,7	7,9	6,7	5,8	5,1	4,6

Fréquences cumulées d'apparition du 1^er chiffre (base 10) (%)
$d$	1	2	3	4	5	6	7	8	9
$f$	30,1	47,7	60,2	69,9	77,8	84,5	90,3	95,4	100

Il existe également une discrète sur-représentation des premiers chiffres en ce qui concerne le second chiffre significatif du nombre. Cette sur-représentation tend à s'annuler au-delà.

Les exemples illustrant cette loi sont nombreux : prenez la suite des 100 premiers carrés ; la fréquence des nombres commençant par 1 est nettement supérieure à la fréquence des carrés commençant par 2, 3, 4, etc. En constituant la liste de 100 nombres, produits de deux ou trois nombres tirés au hasard (dans un grand intervalle), de nouveau la fréquence des nombres commençant par 1 est nettement plus élevée que les autres fréquences.

Les suites numériques qui se comportent exactement comme le stipule la loi de Benford sont, en fait, assez rares. Parmi celles-ci, on peut citer la suite de Fibonacci. Dans la vie réelle, la décroissance des probabilités suivant le premier chiffre est largement constatée, mais la convergence vers les valeurs de la loi de Benford n'est qu'approximative.

Au contraire, cette loi n'est pas vérifiée si la série de données comporte des contraintes quant à l'échelle des valeurs vraisemblables : par exemple, la taille des individus, lorsqu'elle est exprimée dans le système métrique, ne suit, à l'évidence, pas la loi de Benford puisque la quasi totalité des mesures commence par le chiffre « 1 ».

Explication

Les explications les plus classiques supposent que les suites habituelles admettent des caractéristiques particulières.

La forme précise de la loi de Benford peut par exemple être expliquée si l'on admet que les logarithmes des nombres sont uniformément distribués. Cela signifie qu'un nombre a autant de chances d'être entre 100 et 1 000 (logarithme entre 2 et 3) qu'il a de chances de se trouver entre 10 000 et 100 000 (logarithme entre 4 et 5). Pour de nombreux ensembles de nombres, et tout particulièrement ceux qui croissent exponentiellement, comme les chiffres d'affaires d'entreprises et les cours de bourse^{[réf. nécessaire]}, cette supposition est raisonnable.

On peut en particulier l'appuyer par le raisonnement suivant : si une loi générale de distribution des nombres existe, elle doit être indépendante d'un choix d'unité (donc rester valable après multiplication par une constante) et d'un choix de base. L'équidistribution des logarithmes satisfait ces conditions, et est donc un candidat crédible^[7].

Si une variable résulte de la multiplication entre elles d'un grand nombre de variables indépendantes, alors elle suit à peu près la loi de Benford (exactement à la limite)^[8].

Mais ces explications sont à la fois spécifiques (à un certain type de données) et spéculatives (pourquoi supposer que les facteurs agissent multiplicativement ou que le logarithme suit une loi uniforme ?). Récemment, Nicolas Gauvrit et Jean-Paul Delahaye ont proposé une explication plus simple et générale de la loi de Benford^[9]. Selon les chercheurs, c'est le caractère étalé et régulier de la plupart des variables utilisées qui explique la loi de Benford^[10]. Ils suggèrent d'ailleurs qu'un équivalent de cette loi, fondé sur d'autres fonctions que le logarithme, fonctionnerait tout aussi bien.

Ébauche de démonstration^[11]

Choisissons un nombre réel strictement positif appartenant à un intervalle $I$ .

On cherche la probabilité de son premier chiffre non nul, indépendamment de toute autre caractéristique.

Cela correspond à la recherche d'une mesure $m$ sur l'ensemble $I$ , supposé mesurable, avec :

$P(\mathrm{1^{er}~chiffre = 1}) = \frac{m( I\cap\{\ldots\cup[10;20[\cup[1;2[\cup[0.1;0.2[\cup[0.01;0.02[\cup[0.001;0.002[\cup\ldots\})}{m(I)}$
$P(\mathrm{1^{er}~chiffre = 2}) = \frac{m( I\cap\{\ldots\cup[20;30[\cup[2;3[\cup[0.2;0.3[\cup[0.02;0.03[\cup[0.002;0.003[\cup\ldots\})}{m(I)}$
$P(\mathrm{1^{er}~chiffre = 3}) = \frac{m( I\cap\{\ldots\cup[30;40[\cup[3;4[\cup[0.3;0.4[\cup[0.03;0.04[\cup[0.003;0.004[\cup\ldots\})}{m(I)}$
etc.

On suppose que $I$ est construit comme une union de produits de l'intervalle $[1;10[$ par des réels $a i > 0$ ; c'est-à-dire : $I = \cup a i \times [1;10[$ pour des $a i > 0$ . Donc, on travaille dans le groupe multiplicatif des réels strictement positifs (car c'est ainsi que la topologie de ce groupe est construite).

L'ensemble des réels strictement positifs muni de la multiplication étant un groupe topologique séparable et localement compact, il existe une et une seule mesure (à un coefficient multiplicateur près) qui soit invariante par la loi de groupe : la mesure de Haar du groupe.

Cette mesure est $m = d x ⁄ x$ .

Prenons $I = [1;10[$ , on a :

$m(I) = \int_1^{10} \frac{\mathrm dx}{x} = \ln(10) - \ln(1) = \ln(10)$

Et on a :

$P(\mathrm{1^{er}~chiffre} = k) = \frac{m( [k;k+1[)}{m(I)} = \ldots = \frac{\ln(k+1)-\ln(k)}{\ln10} = \frac{\ln(1+\frac{1}{k})}{\ln10}$

Comme la mesure $m$ est invariante par le produit, en prenant $I = \cup a i \times [1;10[$ avec $a i = 10 n$ , on arrive au même résultat.

Notes et références

↑ Hors série de La Recherche sur les nombres, Ted Hill, Le premier chiffre significatif fait sa loi, page 73.
↑ (en) Hal Varian, « Benford's Law », dans The American Statistician, vol. 26, n^o 3, juin 1972, p. 65-66 [texte intégral (page consultée le 27/10/2011)]
↑ Hors série de La Recherche sur les nombres, Ted Hill, Le premier chiffre significatif fait sa loi, page 75.
↑ (en) Bernhard Rauch, Max Göttsche, Gernot Brähler et Stefan Engel, « Fact and Fiction in EU-Governmental Economic Data », dans German Economic Review, vol. 12, n^o 3, août 2011, p. 243-255 [texte intégral (page consultée le 27/10/2011)]
↑ Un économiste soupçonne la Belgique d’avoir falsifié ses comptes - Le Soir, 25 octobre 2011
↑ Joseph Deckert, Mikhail Myagkov et Peter C. Ordeshook Benford's Law and the Detection of Election Fraud Political Analysis (2011) 19(3): 245-268 doi:10.1093/pan/mpr014 lien web
↑ Theodore P. Hill, Base invariance implies Benford's Law, Proceedings of the American Mathematical Society 123, 887-895 (1995). Free web link.
↑ Boyle, J. "An Application of Fourier Series to the Most Significant Digit Problem." Amer. Math. Monthly 101, 879-886, 1994.
↑ http://msh.revues.org/document10363.html
↑ Les distances commencent le plus souvent par le chiffre 1, Science et Vie, août 2010, page 61.
↑ La loi de Benford

Bibliographie

Frank Benford, The law of anomalous numbers, Proceedings of the American Philosophical Society, 78 (1938), p. 551
N. Gauvrit, J.-P. Delahaye, Pourquoi la loi de Benford n'est pas mystérieuse, Mathématiques et Sciences Humaines, 182, été 2008, p7-15.
Ted Hill, The first digit phenomenon, American Scientist 86 (July-August 1998), p. 358.
Hal Varian, Benford's law, American Statistician 26, p.65.
JP Delahaye, L'étonnante loi de Benford, Pour la Science, janvier 2007, p90-95
Joseph Deckert, Mikhail Myagkov et Peter C. Ordeshook Benford's Law and the Detection of Election Fraud Political Analysis (2011) 19(3): 245-268 doi:10.1093/pan/mpr014 lien web

v · Lois de probabilités

Lois discrètes

à support fini	Loi de Bernoulli • Loi uniforme discrète • Loi binomiale • Loi hypergéométrique • Loi de Benford
à support dénombrable	Loi géométrique • Loi de Poisson • Loi binomiale négative • Loi logarithmique

Lois continues

à support compact	Loi uniforme continue • Loi triangulaire • Loi bêta
à support semi-infini	Loi exponentielle • Loi Gamma • Loi du χ² • Loi de Fisher • Loi de Weibull • Loi de Rayleigh • Loi de Rice • Loi d'Erlang • Loi de Lévy • Loi inverse-gamma • Loi log-normale
à support infini	Loi normale • Loi normale asymétrique • Loi de Cauchy • Loi de Laplace • Loi logistique • Loi de Student • Loi stable • Loi de Gumbel

Portail des probabilités et des statistiques

Catégories :

Loi de probabilité
Règle empirique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de Benford de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Loi De Benford — La loi de Benford, également appelée loi des nombres anormaux (car elle est surprenante lorsqu on la découvre), montre que dans une liste de nombre de donnée statistique (par exemple impôt sur le revenu), le 1er chiffre non nul le plus fréquent… … Wikipédia en Français
Loi de benford — La loi de Benford, également appelée loi des nombres anormaux (car elle est surprenante lorsqu on la découvre), montre que dans une liste de nombre de donnée statistique (par exemple impôt sur le revenu), le 1er chiffre non nul le plus fréquent… … Wikipédia en Français
Loi des nombres anormaux — Loi de Benford La loi de Benford, également appelée loi des nombres anormaux (car elle est surprenante lorsqu on la découvre), montre que dans une liste de nombre de donnée statistique (par exemple impôt sur le revenu), le 1er chiffre non nul le… … Wikipédia en Français
Loi De La Controverse De Bendford — Ne doit pas être confondu avec Loi de Benford. La Loi de la controverse de Bendford[1] établie par Gregory Benford, physicien américain de l Université de Californie à Irvine et romancier … Wikipédia en Français
Loi de la controverse de bendford — Ne doit pas être confondu avec Loi de Benford. La Loi de la controverse de Bendford[1] établie par Gregory Benford, physicien américain de l Université de Californie à Irvine et romancier … Wikipédia en Français
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi de la controverse de Bendford — Ne doit pas être confondu avec Loi de Benford. La Loi de la controverse de Bendford[1] établie par Gregory Benford, physicien américain de l Université de Californie à Irvine et romancier[1] … Wikipédia en Français
Loi binomiale — Binomiale Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi de Benford

Sommaire

Historique