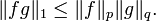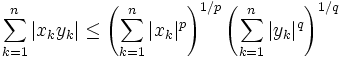Inégalité de hölder

Inégalité de Hölder

En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces L^p : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de L^p(S) et g dans L^q(S). Alors fg appartient à L¹(S) et

$\|fg\|_1 \le \|f\|_p \|g\|_q.$

En considérant S comme l’ensemble {1,...,n} avec la mesure de dénombrement, nous obtenons un cas particulier de l’inégalité, avec p, q < ∞ :

$\sum_{k=1}^n |x_k y_k| \leq \left( \sum_{k=1}^n |x_k|^p \right)^{1/p} \left( \sum_{k=1}^n |y_k|^q \right)^{1/q}$

valable pour tous réels (ou nombres complexes) x₁,...,x_n, y₁,...,y_n.

En considérant S comme l’ensemble des entiers naturels avec la mesure de dénombrement, nous obtenons une inégalité similaire pour les séries.

Pour p = q = 2, nous obtenons l’inégalité de Cauchy-Schwarz.

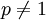L’inégalité de Hölder est utilisée pour démontrer l'inégalité triangulaire dans l’espace L^p, parfois appelée inégalité de Minkowski et aussi pour établir que L^p est le dual de L^q si $p \neq 1$ .

Démonstration

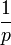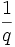La concavité de la fonction logarithme népérien permet d'écrire, pour tout réels strictements positifs a et b, vu que $\frac{1}{p}$ et $\frac{1}{q}$ sont positifs de somme 1: 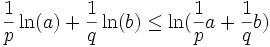$\frac{1}{p}\ln(a)+\frac{1}{q}\ln(b) \leq \ln(\frac{1}{p}a+\frac{1}{q}b)$ , soit encore en prenant l'exponentielle: 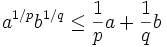$a^{1/p}b^{1/q} \leq \frac{1}{p}a+\frac{1}{q}b$ (1).

Supposons dans un premier temps 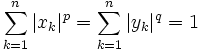$\sum_{k=1}^n |x_k|^p=\sum_{k=1}^n |y_k|^q=1$ . En prenant $a = | x k | p$ et $b = | y k | q$ dans l'inégalité ci-dessus, puis en sommant pour k allant de 1 à n, on obtient 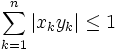$\sum_{k=1}^n |x_k y_k| \leq 1$ (2).

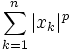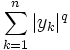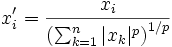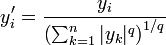Supposons désormais simplement que $\sum_{k=1}^n |x_k|^p$ et $\sum_{k=1}^n |y_k|^q$ sont non nuls (i.e. l'un au moins des $x k$ et l'un au moins des $y k$ sont non nuls). En posant $x'_{i}=\frac{x_{i}}{\left( \sum_{k=1}^n |x_k|^p \right)^{1/p}}$ et $y'_{i}=\frac{y_{i}}{\left( \sum_{k=1}^n |y_k|^q \right)^{1/q}}$ on peut appliquer l'inégalité (2) avec les $x' i$ et $y' i$ , ce qui donne l'inégalité de Hölder. Enfin, elle est évidente si tous les $x k$ ou tous les $y k$ sont nuls.

Il y a une généralisation de cette inégalité :

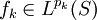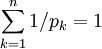Soient ${f}_k \in {L}^{p_k}(S)$ avec $\sum_{k=1}^n 1/p_k =1$ , alors :

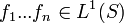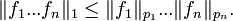
On a ${f}_1...{f}_n \in {L}^1(S)$ et $\|f_1...f_n\|_1 \le \|f_1\|_{p_1} ... \|f_n\|_{p_n}.$

Voir aussi

Bibliographie

Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]

Articles en rapport avec la convexité
Géométrie convexe	Article principal : Ensemble convexe Outils et résultats fondamentaux : Enveloppe convexe • Adhérence, intérieur et frontière d'un convexe • Projection sur un convexe fermé • Séparation des convexes • Points remarquables à la frontière d'un convexe • Polytope • Théorème de Krein-Milman • Lemme de Farkas Géométrie combinatoire : Théorème de Carathéodory • Théorème de Radon • Théorème de Helly Géométrie métrique : Courbe de largeur constante • Théorème des quatre sommets Algorithmes de géométrie convexe : Approche polyèdrale • Marche de Jarvis • Parcours de Graham • Théorème optimisation/séparation Optimisation linéaire : Programmation linéaire • Algorithme du simplexe • Génération de colonnes
Interactions géométrie-analyse	Théorème de Hahn-Banach • Jauge
Analyse convexe	Article principal : Fonction convexe Outils et résultats fondamentaux : Inégalité de Jensen Optimisation convexe : Conditions de Kuhn-Tucker • Méthode du point intérieur
Utilisations de la convexité	Inégalités de convexité : Inégalité arithmético-géométrique • Inégalité de Hölder Analyse fonctionnelle : Espace localement convexe • Théorème du point fixe de Schauder Localisation de zéros de polynômes : Théorème de Gauss-Lucas Théorie des nombres : Théorème de Minkowski

Portail des mathématiques

Ce document provient de « In%C3%A9galit%C3%A9 de H%C3%B6lder ».

Catégories : Théorie de la mesure | Inégalité | Analyse convexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité de hölder de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Inegalite de Holder — Inégalité de Hölder En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans… … Wikipédia en Français
Inégalité De Hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
Inégalité de Hölder — En analyse, l’inégalité de Hölder, ainsi nommée en l honneur de Otto Hölder, est une inégalité fondamentale relative aux espaces de fonctions Lp et aux espaces de suites . Sommaire 1 Enoncé 2 Applications … Wikipédia en Français
Inegalite de Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité De Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inégalité de cauchy-schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inegalite de Jensen — Inégalité de Jensen En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de … Wikipédia en Français
Inégalité De Jensen — En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de deux manières … Wikipédia en Français
Inégalité de jensen — En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de deux manières … Wikipédia en Français
Inegalite arithmetico-geometrique — Inégalité arithmético géométrique Étant donnés n réels strictement positifs , on définit leur moyenne arithmétique et leur moyenne géométrique : et . Il est classique que … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Inégalité de hölder