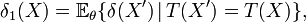- Inégalité De Jensen
-
Inégalité de Jensen
En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l'écrire de deux manières : discrète ou intégrale. Elle apparaît notamment en analyse, en théorie de la mesure et en probabilités (théorème de Rao-Blackwell), mais également en physique statistique, en mécanique quantique et en théorie de l'information (inégalité de Gibbs).
Pour les fonctions concaves, cette inégalité reste vraie si elle est renversée. Ce sera notamment le cas pour la fonction logarithme, très utilisée en physique.
Sommaire
Énoncé
Forme discrète
Inégalité de Convexité — Soit f une fonction convexe. Soit (x1, ..., xn) une famille de réels appartenant à l'intervalle de définition de f. Soit (λ1, ..., λn) une famille de réels de l'intervalle [0; 1] tels que :
Alors on a :
De nombreux résultats élémentaires importants d'analyse s'en déduisent, comme l'inégalité arithmético-géométrique : si
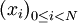 est une famille de réels strictement positifs, alors :
est une famille de réels strictement positifs, alors :Donc la preuve découle immédiatement de l'inégalité de Jensen (renversée), appliqué au logarithme de la partie de droite, le logarithme étant concave.
Forme intégrale
Cadre général
Inégalité de Jensen — Soit a et b deux éléments de
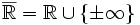 tels que a < b. Soit
tels que a < b. Soit  une fonction continue de [0; 1] dans ]a; b[. Soit enfin
une fonction continue de [0; 1] dans ]a; b[. Soit enfin 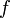 une fonction convexe de ]a; b[ à valeurs réelles. Alors :
une fonction convexe de ]a; b[ à valeurs réelles. Alors :On en déduit une relation importante entre les espaces Lp associés à une mesure finie : si p et q sont deux entiers naturels non-nuls et tels que
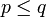 , alors :
, alors :Théorie de la mesure
Inégalité de Jensen — Soit (Ω,A,μ) un espace mesuré tel que μ(Ω) = 1. Si g est une fonction à valeurs réelles μ-intégrable et si φ est une fonction convexe mesurable sur les réels, alors :
Probabilités, statistiques
En statistiques, on retrouve cette inégalité concernant l'espérance :
Inégalité de Jensen — Soit f une fonction convexe sur ]a; b[ et X une variable aléatoire d'espérance finie, à valeurs dans ]a; b[. Alors l'inégalité suivante est vraie :
Avec
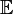 l'espérance mathématique.
l'espérance mathématique.On peut alors en déduire un résultat important de statistiques : le théorème de Rao-Blackwell. En effet, si L est une fonction convexe, alors d'après l'inégalité de Jensen,
Si δ(X) est un estimateur d'un paramètre non observé θ étant donné un vecteur X des observables, et si T(X) est une statistique suffisante pour θ, alors un estimateur plus performant, dans le sens de la minimisation des pertes, est donné par :
C'est-à-dire l'espérance de δ par rapport à θ, prise sur tous les vecteurs X compatibles avec la même valeur de T(X).
Démonstration
La démonstration historique est une preuve par récurrence de la forme discrète. La forme intégrale se déduit dans le cadre de la théorie de la mesure par des arguments de densité, et se généralise ensuite aux autres contextes.
Voici une preuve plus simple, dans le cadre le plus général : celui des espaces mesurés.Soient (Ω,A,μ) un espace mesuré tel que μ(Ω) = 1,
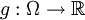 μ-intégrable et
μ-intégrable et 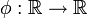 mesurable convexe.
mesurable convexe.On note Λφ l'ensemble des applications affines de
 dans
dans  inférieures à φ.
inférieures à φ.Les propriétés des fonctions convexes assurent que pour
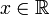 ,
, 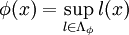 .
.En particulier, pour
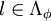 ,
, 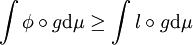 .
.Or, pour
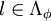 ,
,  , car μ(Ω) = 1.
, car μ(Ω) = 1.En passant à la borne supérieure sur l, on obtient l'inégalité :
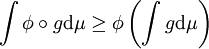
Toutes les autres formes de l'inégalité de Jensen s'en déduisent.
Notes et références
- ↑ (fr) Johan Jensen : « Sur les fonctions convexes et les inégalités entre les valeurs moyennes », Acta Mathematica 30 : 175-193, 1906.
- ↑ Dans le cas le plus général, on peut ne pas imposer cette relation aux λi, mais il faut alors dans l'inégalité de Jensen diviser les sommes par
 .
.
Voir aussi
- Portail des mathématiques
Catégories : Analyse convexe | Inégalité
Wikimedia Foundation. 2010.

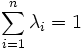
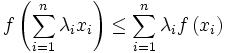
![\frac{1}{N} \sum_{i=0}^{N-1} x_i \ge \sqrt[N]{\prod_{i=0}^{N-1} x_i}](/pictures/frwiki/98/bed409bbdc9c4202fb0c4929c0509377.png)
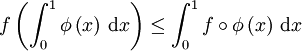
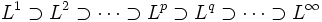
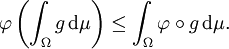
![f(\mathbb{E}(X)) \leq \mathbb{E}[f(X)]](/pictures/frwiki/49/137134a5624eee429c6948a190da22c6.png)