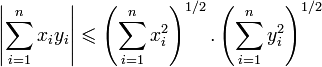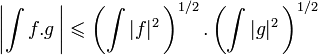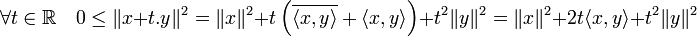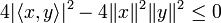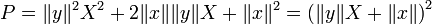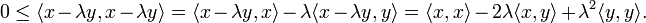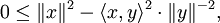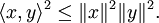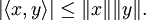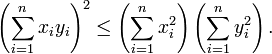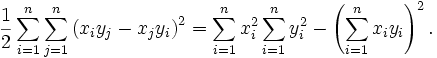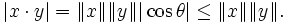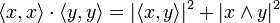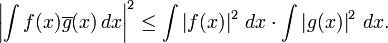Inégalité de cauchy-schwarz

Inégalité de Cauchy-Schwarz

Pour les articles homonymes, voir Cauchy et Schwarz.

En mathématiques, l'inégalité de Cauchy-Schwarz, aussi appelée inégalité de Schwarz^[1], ou encore inégalité de Cauchy-Bunyakovski-Schwarz^[2], se rencontre dans de nombreux domaines tels que l'algèbre linéaire avec les vecteurs, l'analyse avec les séries et en intégration avec les intégrales de produits.

Cette inégalité s'applique dans le cas d'un espace vectoriel sur le corps des nombres réels ou complexes munis d'un produit scalaire. Dans le cas complexe, le produit scalaire désigne une forme hermitienne définie positive. Son contexte général est donc celui d'un espace préhilbertien.

Cette inégalité possède de nombreuses applications, comme le fait d'établir l'inégalité de Minkowski montrant que la racine carrée de la forme quadratique associée au produit scalaire est une norme, ou encore que le produit scalaire est continu.

Elle doit son nom à Hermann Amandus Schwarz^[3] et à Augustin Louis Cauchy^[4].

Sommaire

1 Définition
2 Conséquences
3 Démonstration
4 Inégalité de Cauchy-Schwarz dans des cas particuliers
- 4.1 Dans
- 4.2 Dans
5 Références

Définition

L'inégalité s'énonce de la façon suivante :

Pour tout x et y éléments d'un espace préhilbertien réel ou complexe

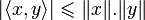
$|\langle x,y\rangle|\leqslant \|x\|.\|y\|$

Les deux membres sont égaux si et seulement si x et y sont linéairement dépendants.

Conséquences

Une conséquence de l'inégalité de Cauchy-Schwarz est que le produit scalaire est une fonction continue.

Dans le cas de l'espace euclidien 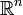$\quad \mathbb R ^n$ muni du produit scalaire canonique, l'inégalité de Cauchy-Schwarz s'écrit :

$\left|\sum_{i=1}^n x_{i}y_{i}\right|\leqslant\left (\sum_{i=1}^n x_{i}^{2}\right)^{1/2}.\left (\sum_{i=1}^n y_{i}^{2}\right)^{1/2}$

Dans le cas des fonctions à valeurs complexes de carré intégrable, l'inégalité de Cauchy-Schwarz s'écrit :

$\left|\int f. g\, \right| \leqslant \left( \int |f|^2\,\right)^{1/2}. \left( \int |g|^2\, \right)^{1/2}$

Ces deux dernières formulations sont généralisées par l'inégalité de Hölder.

Démonstration

Démontrons le résultat dans le cas d'un préhilbertien complexe.

Inégalité

Soit (x,y) un couple de vecteurs. Quitte à multiplier x par un scalaire de la forme $e i θ$ , avec $θ$ réel, on peut supposer que le produit 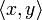$\langle x,y\rangle$ est réel, et on obtient :

$\forall t \in \mathbb{R} \quad 0 \leq \|x+t.y\|^2 = \|x\|^2+ t \left(\overline{\langle x,y\rangle} + \langle x,y\rangle\right) + t^2\|y\|^2= \|x\|^2 + 2t\langle x,y\rangle + t^2\|y\|^2$

Ainsi, le polynôme à coefficients réels 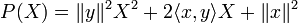$P(X)=\|y\|^2 X^2 + 2\langle x,y\rangle X + \|x\|^2$ d'inconnue X, est positif sur $\mathbb{R}$ d'après la relation précédente. Il ne peut donc pas avoir deux racines réelles distinctes. Ceci implique que son discriminant est négatif. On obtient:

$4|\langle x,y\rangle |^2 - 4\|x\|^2\|y\|^2 \le 0$

Ce qui entraîne bien l'inégalité annoncée.

Cas d'égalité

Si les vecteurs x et y sont liés, on peut sans perte de généralité supposer que 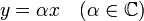$y=\alpha x \quad (\alpha \in \mathbb{C})$ . On en déduit immédiatement: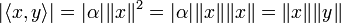 $\quad |\langle x,y\rangle |=|\alpha|\|x\|^2=|\alpha|\|x\|\|x\|=\|x\|\|y\|$

Réciproquement, supposons qu'on ait l'égalité 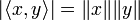$\quad |\langle x,y\rangle |=\|x\|\|y\|$ Si y=0, les vecteurs sont liés. Si y 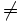$\not=$ 0, le polynôme ci-dessus s'écrit :

$P=\|y\|^2 X^2 + 2\|x\|\|y\| X + \|x\|^2 = \left(\|y\| X +\|x\|\right)^2$

Il admet pour racine réelle double 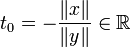$t_0=-\frac{\|x\|}{\|y\|}\in\mathbb{R}$ , d'où 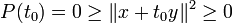$P(t_0) = 0 \geq \|x+t_0 y\|^2\geq 0$ , puis $x + t 0 y = 0$ . D'où le résultat.

Cas réel

Dans le cas d'un espace réel la démonstration est analogue. On peut aussi proposer une preuve légèrement différente :

La preuve pour $y = 0$ est triviale, on considère donc 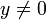$y \neq 0$ . Pour 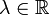$\lambda \in \mathbb{R}$ on a :

$0 \leq \langle x-\lambda y,x-\lambda y \rangle = \langle x-\lambda y,x \rangle - \lambda \langle x-\lambda y,y \rangle = \langle x,x \rangle -2\lambda \langle x,y \rangle + \lambda^2 \langle y,y \rangle.$

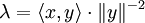Prenons $\lambda = \langle x,y \rangle \cdot \|y\|^{-2}$ de sorte que :

$0 \leq \|x\| ^2 - \langle x,y \rangle^2 \cdot \|y\|^{-2},$

Ainsi

$\langle x,y \rangle^2 \leq \|x\|^2 \|y\|^2.$

Puis

$\big| \langle x,y \rangle \big| \leq \|x\| \|y\|.$

Cette preuve peut facilement être adaptée au cas complexe.

Inégalité de Cauchy-Schwarz dans des cas particuliers

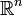
Dans $\mathbb{R}^n\,$

Dans l'espace euclidien 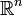$\mathbb{R}^n\,$ muni du produit scalaire usuel, l'inégalité de Cauchy-Schwarz s'écrit:

$\left(\sum_{i=1}^n x_i y_i\right)^2\leq \left(\sum_{i=1}^n x_i^2\right) \left(\sum_{i=1}^n y_i^2\right).$

Dans ce cas particulier, il est possible de démontrer l'inégalité de la manière suivante: considérons le polynôme en $z$ suivant:

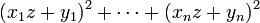
$(x_1 z + y_1)^2 + \cdots + (x_n z + y_n)^2$

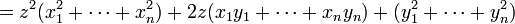
$= z^2(x_1^2 + \cdots + x_n^2) + 2z(x_1y_1 + \cdots + x_ny_n) + (y_1^2 +\cdots + y_n^2)$

Remarquons que ce polynôme est du second degré en $z$ . Puisque ce polynôme est positif, il n'a de racines que lorsque tous les quotients $x i / y i$ soient égaux. Ainsi son discriminant est inférieur à zéro, ce qui implique que

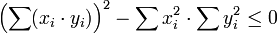$\left(\sum ( x_i \cdot y_i ) \right)^2 - \sum {x_i^2} \cdot \sum {y_i^2} \le 0$ ,

qui n'est autre que l'inégalité de Cauchy-Schwarz.

Une démonstration équivalente pour 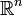$\mathbb{R}^n\,$ commence avec la sommation ci-dessous.

En développant les parenthèses, nous avons:

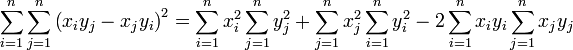$\sum_{i=1}^n \sum_{j=1}^n \left( x_i y_j - x_j y_i \right)^2 = \sum_{i=1}^n x_i^2 \sum_{j=1}^n y_j^2 + \sum_{j=1}^n x_j^2 \sum_{i=1}^n y_i^2 - 2 \sum_{i=1}^n x_i y_i \sum_{j=1}^n x_j y_j$ ,

et en regroupant les termes identiques (bien qu'ayant des indices de sommation différents) nous obtenons:

$\frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \left( x_i y_j - x_j y_i \right)^2 = \sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n x_i y_i \right)^2 .$

Comme le côté gauche de l'équation est une somme de carrés de nombres réels, il est supérieur ou égal à zéro, donc:

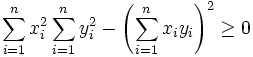$\sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n x_i y_i \right)^2 \geq 0$ .

Aussi, lorsque $n = 2$ or 3, le produit scalaire est proportionnel à l'angle entre les deux vecteurs, et l'on peut obtenir immédiatement l'inégalité:

$|x \cdot y| = \|x\| \|y\| | \cos \theta | \le \|x\| \|y\|.$

En outre, dans ce cas, l'inégalité de Cauchy-Schwarz peut également être déduite de l'identité de Lagrange. Pour $n = 3$ , l'identité de Lagrange s'écrit

$\langle x,x\rangle \cdot \langle y,y\rangle = |\langle x,y\rangle|^2 + |x \wedge y|^2$

d'où résulte facilement Cauchy-Schwarz.

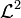
Dans $\mathcal{L}^2$

Pour le produit scalaire de l'espace vectoriel des fonctions à valeur complexes de carré intégrable, on a

$\left|\int f(x) \overline{g}(x)\,dx\right|^2\leq\int \left|f(x)\right|^2\,dx \cdot \int\left|g(x)\right|^2\,dx.$

Une généralisation de cela est l'inégalité de Hölder.

Références

Notes

↑ On trouve par exemple cette expression chez S. Lang Analyse Réelle InterEditions, Paris 1977 (ISBN 2729600595) p 148
↑ Par exemple O. A. Ladyzhenskaya The boundary value problems of mathematical physics Springer-Verlag 1985 (ISBN 3-540-90989-3) p 2
↑ Hermann Amandus Schwarz Ueber ein Flachen kleinsten Flacheninhalts betreffendes Problem der Variationsrechnung Acta Societatis scientiarum Fennicae Vol XV p 318 1888 Lire
↑ Augustin Louis Cauchy Oeuvres 2 III p 373 1821

Liens externes

(fr) Inégalité de Cauchy-Schwarz par DicoMaths
(fr) Espaces préhilbertiens complexes par Les-Mathématiques.net
(fr) Espaces euclidiens par F. Wlazinski de l'Université de Picardie

Référence

Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Portail des mathématiques

Ce document provient de « In%C3%A9galit%C3%A9 de Cauchy-Schwarz ».

Catégories : Algèbre bilinéaire | Inégalité | Géométrie euclidienne

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité de cauchy-schwarz de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Inegalite de Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité De Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inégalité de Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. Ne doit pas être confondu avec Inégalité de Cauchy. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1 … Wikipédia en Français
Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité de Cauchy — Pour les articles homonymes, voir Cauchy. Ne doit pas être confondu avec Inégalité de Cauchy Schwarz. L inégalité de Cauchy, établie par Augustin Louis Cauchy, est une relation permettant d estimer les dérivées d une fonction holomorphe.… … Wikipédia en Français
Inegalite triangulaire — Inégalité triangulaire Triangle En mathématiques, l inégalité triangulaire exprime en substance que le chemin direct est le plus court. Cette inégalité peut être énoncée sous la forme d une propriété ou bien d une condition nécessaire à la bonne… … Wikipédia en Français
Inégalité Triangulaire — Triangle En mathématiques, l inégalité triangulaire exprime en substance que le chemin direct est le plus court. Cette inégalité peut être énoncée sous la forme d une propriété ou bien d une condition nécessaire à la bonne définition d une… … Wikipédia en Français
Inegalite de Holder — Inégalité de Hölder En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans… … Wikipédia en Français
Inégalité De Hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
Inégalité de hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Inégalité de cauchy-schwarz

Inégalité de Cauchy-Schwarz

Sommaire

Définition

Conséquences