Loi de similitude

Loi de similitude

Grandeur sans dimension

En physique, une grandeur sans dimension est une quantité permettant de décrire une caractéristique physique sans dimension ni unité explicite d'expression. Elle est constituée du produit ou rapport de grandeurs à dimensions, de telle façon que le rapport des unités équivaut à un. L'analyse dimensionnelle permet de définir ces grandeurs sans dimension. L'unité SI dérivée associée est le nombre 1[1]. On trouve parmi ces grandeurs l'indice de réfraction ou la densité par exemple.

Ces grandeurs sans dimension interviennent particulièrement en mécanique des fluides et pour la description de phénomène de transfert lorsqu'on utilise la similitude de modèles réduits ou théorie des maquettes et construit l'interprétation des résultats d'essais. Elles portent le nom de nombres sans dimension, nombres adimensionnels, ou encore de nombres caractéristiques.

Sommaire

Des nombres caractéristiques utiles

Le domaine d'application par excellence des nombres adimensionnels est la mécanique des fluides. Il existe des centaines de nombres dont une grande partie réservée à des sujets très spécialisés[2]. Une liste non-exhaustive est donnée ci-après des nombres adimensionnels les plus courants.

Liste commune

Liste des nombres adimensionnels
Nom Symbole Domaines d'utilisation Type de rapport
Nombre d'Abbe V Optique angle de réfraction/angle de dispersion
Nombre d'absorption Ab Transfert de masse temps d'exposition/temps d'absorption
Nombre d'accélération Ac Mécanique des fluides force d'accélération/force de gravité
Nombre d'Alfven Al Magnétohydrodynamique vitesse du fluide/vitesse de l'onde d'Alfven
Nombre d'Archimède Ar Mécanique des fluides force de gravité*force d'inertie/force visqueuse2
Nombre d'Atwood At Mécanique des fluides différence de densités/somme de densité
Nombre de Bagnold Ba Mécanique des fluides, rhéologie énergie dissipée par frottement visqueux/énergie dissipée par choc
Nombre de Bansen Ba Transfert thermique énergie transférée par radiation/capacité thermique du fluide
Nombre de Bejan Be Mécanique des fluides, transfert thermique, Thermodynamique entropie générée par transfert de chaleur /entropie totale générée
Nombre de Bingham Bm Mécanique des fluides limite d'élasticité/force visqueuse
Nombre de Biot Bi Transfert thermique transfert thermique dans un corps/transfert thermique à la surface du corps
Nombre de Blake Bl Mécanique des fluides force d'inertie/force visqueuse (nombre de Reynolds pour lit de particule)
Nombre de Bodenstein Bo Transfert de masse, mécanique des fluides transfert de masse convectif/transfert de masse par dispersion
Nombre de Boltzmann Bo Transfert thermique Equivalent au nombre de Thring
Nombre de Bond Bo Mécanique des fluides force de gravité/tension superficielle
Nombre de Boussinesq Bq Mécanique des fluides force d'inertie/force de gravité
Nombre de Brinkman Br Transfert thermique, rhéologie chaleur produite par dissipation des forces visqueuses dissipée/chaleur transférée par conduction
Nombre de Bulygin Bu Transfert thermique énergie utilisée pour évaporer le liquide/énergie utilisée pour chauffer le corps mouillé
Nombre capillaire Ca Mécanique des fluides force visqueuse/tension superficielle
Nombre de capillarité Cap Mécanique des fluides force capillaire/force de filtration
Nombre de Cauchy Ca Rhéologie force d'inertie/force élastique
Nombre de cavitation σc Mécanique des fluides différence de pression/pression dynamique
Nombre de Clausius Cl Transfert thermique
Facteur J de Colburn jH, jM Transfert thermique, de masse, de moment
Nombre de condensation Co Transfert thermique force visqueuse/force de gravité
Nombre de Courant Co Mathématiques, informatique
Nombre de Cowling Co Magnétohydrodynamique vitesse de l'onde d'Alfven/vitesse du fluide
Nombre de Damköhler Da Cinétique chimique vitesse de réaction chimique/vitesse de transfert des réactifs
Nombre de Dean D Mécanique des fluides force d'inertie/force visqueuse (nombre de Reynolds pour tube courbe)
Densité d Physique, chimie, biologie masse volumique du corps/masse volumique du corps de référence (Pression et Température identiques pour des corps gazeux)
Nombre de Deborah De Rhéologie temps de relaxation d'un corps/temps de l'expérience
Nombre de Dufour Du2 Transfert thermique Chaleur transférée par diffusion/Chaleur transférée par convection (lorsque transfert par diffusion et par conduction sont égaux)
Nombre de Dulong Du Mécanique des fluides Equivalent au nombre d'Eckert
Nombre d'Eckert Ec Mécanique des fluides énergie cinétique d'un fluide/enthalpie du fluide
Nombre d'Einstein Ei Magnétohydrodynamique Equivalent au nombre de Lorentz
Nombre d'Ekman Ek Mécanique des fluides force visqueuse/force de Coriolis
Nombre d'Ellis El Mécanique des fluide
Nombre d'Elsasser El,Λ Magnétohydrodynamique force de Lorentz/force de Coriolis
Nombre d'Eötvös Eo Mécanique des fluides cf. Nombre de Bond
Nombre d'Ericksen Er Rhéologie
Nombre d'Euler (physique) Eu Mécanique des fluides force de pression/force d'inertie
Nombre d'évaporation E Transfert thermique
Nombre de Fedorov Fe Mécanique des fluides flux de particules/flux gaz porteur (lit fluidisé)
Nombre de Fourier Fo Transfert thermique transfert thermique par conduction/accumulation d'énergie
Nombre de Fresnel F Optique
Nombre de Froude Fr Mécanique des fluides force d'inertie/force de gravité
Nombre de Galilée Ga Mécanique des fluides portance/force d'inertie (cf. nombre d'Archimède)
Nombre de Gay-Lussac Gc Transfert thermique différence de température/coefficient d'augmentation de pression isochore
Nombre de Goucher Go Mécanique des fluides (force de gravité/tension superficielle)0.5
Nombre de Graetz Gz Transfert thermique capacité thermique du fluide/chaleur transférée par conduction
Nombre de Grashof Gr Mécanique des fluides portance thermique/force d'inertie
Nombre de Gukhman Gu Transfert thermique critère pour transfert thermique convectif par évaporation
Nombre de Hagen Ha Mécanique des fluides
Nombre de Hartmann Ha Magnétohydrodynamique force de Laplace/force visqueuse
Nombre de Hatta Ha Cinétique chimique vitesse de réaction chimique sans transfert de masse/transfert de masse
Nombre de Hedström He Rhéologie limite de plasticité*force d'inertie/force visqueuse2
Nombre de Helmholtz He Acoustique longueur caractéristique/longueur d'onde
Nombre de Hersey Hs Tribologie Inverse du nombre de Stokes
Nombre de Hodgson Ho Mesure constante de temps du système/période de pulsation
Nombre de Jakob Ja Transfert thermique chaleur sensible/chaleur latente (vaporisation)
Nombre de Jeffreys Je Mécanique des fluides, géophysique force gravitationnelle/force visqueuse
Nombre de Joule Jo Magnétisme énergie thermique par effet Joule/énergie du champ magnétique
Nombre de Karlovitz Ka Mécanique des fluides temps chimique/temps de Kolmogorov
Nombre de Karman Ka Mécanique des fluides Mesure de la turbulence dans un flux
Nombre de Keulegan-Carpenter KC Mécanique des fluides
Nombre de Kirpichev Ki Transfert thermique, de masse transfert en surface/ transfert dans le solide
Nombre de Knudsen Kn Mécanique des fluides distance libre/longueur caractéristique
Nombre de Kossovitch Ko Transfert thermique chaleur pour évaporer eau/chaleur pour chauffer corps mouillé
Nombre de Kutateladze Ku Transfert thermique
Nombre de Laplace La Mécanique des fluides tension superficielle et forces d'inertie/forces visqueuse (cf. nombre d'Ohnesorge)
Nombre de Laval La
Nombre de Leroux L Mécanique des fluides Equivalent au nombre de cavitation
Nombre de Lewis Le Transfert de masse et thermique diffusivité massique/diffusivité thermique
Nombre de Lorentz Lo Magnétohydrodynamique vitesse/vitesse de la lumière
Nombre de Luikov Lu Transfert thermique et de masse
Nombre de Lukomskii Lu
Nombre de Lundquist Lu Magnétohydrodynamique vitesse d'Alfvén/vitesse de diffusion résistive
Nombre de Lyashchenko Ly Mécanique des fluides (force d'inertie)/(force visqueuese*force de gravité)
Nombre de Lykoudis Ly Magnétisme, mécanique des fluides
Nombre de Mach Ma Mécanique des fluides vitesse du fluide/vitesse du son
Nombre de Marangoni Mg Transfert thermique, mécanique des fluides
Nombre de Margoulis Ms Transfert thermique, transfert de masse Equivalent au nombre de Stanton
Nombre de Margulis Mr Transfert thermique, transfert de masse Equivalent au nombre de Stanton
Nombre de Merkel Me Transfert de masse masse d'eau transférée par unité de différence d'humidité/masse de gaz sec
Nombre de Miniovich Mn Porosité taille des pores/porosité
Nombre de Mondt Mo Transfert de chaleur chaleur transférée par convection/chaleur transférée par conduction longitudinale dans surface d'échange
Nombre de Morton Mo Mécanique des fluides
Nombre de Naze Na Magnétohydrodynamique vitesse d'Alfven/vitesse du son
Nombre de Nahme Na Rhéologie
Nombre de Newton Ne Mécanique des fluides force de résistance/force d'inertie
Nombre de Nusselt Nu Transfert thermique transfert thermique total/transfert thermique par conduction
Nombre d'Ocvirk Oc
Nombre d'Ohnesorge Oh Mécanique des fluides force visqueuses/tension superficielle et force d'inertie
Nombre de Péclet Pe Transfert thermique et de masse transfert par convection/transfert par diffusion ou conduction
Nombre de Peel
Nombre de pipeline pn Mécanique des fluides
Nombre de plasticité Np Rhéologie Equivalent au nombre de Bingham
Nombre de Poiseuille Ps Mécanique des fluides /force visqueuse
Nombre de Posnov Pn Transfert thermique et de masse
Nombre de Pomerantsev Pm Transfert thermique Equivalent au nombre de Damköhler
Nombre de Prater
Nombre de Prandtl Pr Mécanique des fluides, transfert thermique diffusivité de moment/diffusivité thermique
Nombre de Predvoditelev Pd Transfert thermique changement de température d'un fluide/changement de température d'un corps immergé dans le fluide
Nombre de pression Kp Mécanique des fluides pression absolu/différence de pression à travers une surface
Nombre de puissance Np Mécanique des fluides force d'entraînement(agitateur)/force d'inertie
Nombre de radiation Nr Transfert thermique
Nombre de Ramzin Ks Transfert thermique
Nombre de Rayleigh Ra Mécanique des fluides convection naturelle/diffusion
Nombre de Reech Re Mécanique de fluide force de gravité/force d'inertie
Nombre de Reynolds Re Mécanique des fluides force d'inertie/force visqueuse
Nombre de Richardson Ri Mécanique des fluides
Nombre global de Richardson BRN Météorologie Énergie potentielle de convection disponible/cisaillement vertical des vents dans un orage
Nombre de Romankov Ro Transfert thermique
Nombre de Roshko Ro Mécanique des fluides Equivalent au nombre de Stokes
Nombre de Rossby Ro Mécanique des fluides force d'inertie/force de Coriolis
Nombre de Rouse R Mécanique des fluides, transport sédimentaire vitesse de chute / vitesse de frottement
Nombre de Russell Ru
Nombre de Sachs Sa Explosion
Nombre de Sarrau Sa Mécanique des fluides Equivalent au nombre de Mach
Nombre de Schiller Sch Mécanique des fluides force d'inertie/(force visqueuse*coefficient de traînée)
Nombre de Schmidt Sc Mécanique des fluides, transfert de masse diffusivité de moment/diffusivité massique
Nombre de Semenov Sm Transfert de masse et thermique Equivalent au nombre de Lewis
Nombre de Sherwood Sh Transfert de masse transfert massique total/transfert massique par diffusion
Nombre de Sommerfeld S
Nombre de Spalding B
Nombre de Stanton St Transfert thermique et de masse transfert total/transfert par convection
Nombre de Stefan Se Transfert thermique chaleur sensible/chaleur latente (fusion)
Nombre de Stewart St,N Magnétohydrodynamique force magnétique/force d'inertie
Nombre de Stokes S Mécanique des fluides force d'inertie particule/force d'entraînement(fluide)
Nombre de Strouhal Sr Mécanique des fluides
Nombre de Stuart St,N Magnétohydrodynamique Equivalent au nombre de Stewart
Nombre de Suratman Su Mécanique des fluides Equivalent au nombre de Laplace
Nombre de Taylor Ta Mécanique des fluides force centrifuge/force visqueuse
Nombre de Thiele mT, ϕ Cinétique chimique, transfert de masse vitesse de réaction chimique/flux diffusif des réactifs vers le catalyseur
Nombre de Thoma
Nombre de Thomson Th Mécanique des fluides Equivalent au nombre de Strouhal
Nombre de Thring Th Transfert thermique capacité thermique du fluide/chaleur transférée par radiation
Nombre de Weber We Mécanique des fluides forces d'inertie/tension superficielle
Nombre de Weissenberg Wi Rhéologie temps de relaxation d'un corps/temps de l'expérience
Nombre de Womersley Wo Mécanique des fluides force d'inertie instationnaire/force visqueuse

Nombre adimensionel en cosmologie

Similitude des modèles réduits

Généralités

Divers domaines d'études conduisent à des expériences sur des modèles réduits, ce qui pose le problème de leur réalisme : les phénomènes aux deux échelles doivent être semblables. Par exemple, dans l'étude d'un écoulement autour d'un obstacle le sillage doit comporter, à l'échelle près, le même système de tourbillons ou de turbulence sur le modèle et sur le prototype.

Dire que les phénomènes sont semblables revient à dire que certains invariants doivent être conservés lorsqu'on change d'échelle. Ces invariants sont donc des nombres sans dimension qui doivent être construits à partir des grandeurs dimensionnelles qui caractérisent le phénomène. Dans ce qui suit, le cas des problèmes mécaniques, dans lesquels les trois grandeurs fondamentales sont la masse M, la longueur L et le temps T, sera seul considéré.

Dans ces conditions, toute grandeur physique est homogène à une expression de la forme Mα Lβ Tγ. Pour un nombre sans dimension, les exposants de chaque grandeur doivent être nuls.

Le premier problème consiste à déterminer quelles sont les grandeurs qui régissent le phénomène et celles qui sont négligeables (l'oubli d'une grandeur essentielle peut conduire à des résultats totalement erronés). Une fois que cette liste est établie, il faut en déduire les nombres sans dimension dont la conservation assurera la similitude.

Parmi ces nombres sans dimension, certains sont des rapports de longueurs : leur conservation caractérise la similitude géométrique qui n'appelle pas de commentaires particuliers. Seuls ceux qui font intervenir des grandeurs physiques présentent ici un intérêt.

Exemples

Dans l'étude de l'écoulement des fluides visqueux, on peut obtenir des résultats intéressants à partir de considérations simples basées sur les formules de dimensions des grandeurs physiques concernées. Dans le cas du mouvement d'un corps de forme donnée, la détermination complète n'exige la connaissance que de l'une de ses dimensions linéaires (rayon d'un sphère ou d'un tube de cylindre, longueur de l'un des demi-axes d'un ellipsoïde de révolution d'excentricité donnée, etc).

Prenons le cas d'écoulement permanent. Si l'on se réfère à l'équation de Navier-Stokes, les paramètres caractérisant le fluide sont: la viscosité cinématique ν = η / ρ et les fonctions inconnues fournies par la résolution, c'est-à-dire la vitesse \vec{v} et le rapport p / ρ. L'écoulement dépend encore de la forme caractérisée par la dimension linéaire D. On vérifie aisément qu'à l'aide des grandeurs V, D et ν, on peut former qu'une seule combinaison indépendante sans dimension. Cette combinaison sans dimension est le nombre de Reynolds:

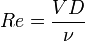
Re = {{V D} \over \nu}

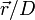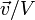Tout autre paramètre sans dimension peut être représenté par une fonction de Re. Si l'on mesure les longueurs en unité D et les vitesses en unité V revient à introduire les quantités sans dimension: \vec{r} / D et \vec{v} / V. Comme le seul paramètre sans dimension est le nombre de Reynolds, on conçoit que la distribution des vitesses résultant de la résolution des équations hydrodynamiques soit décrite par des fonctions de la forme: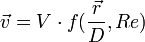

\vec{v} = V \cdot f({\vec{r} \over D}, Re)

Cette expression montre que dans deux écoulements différents mais du même type les vitesses 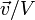\vec{v} / V sont des fonctions identiques du rapport 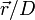\vec{r} / D à condition que les nombres de Reynolds de ces écoulements soient les mêmes. Les modifications de l'échelle de mesure des coordonnées et des vitesses sont dits semblables. Par conséquent, deux écoulements de même type, caractérisés par le même nombre de Reynolds sont semblables. C'est la loi dite de similitude énoncé par O. Reynolds en 1883.

Une formule analogue peut être établie en ce qui concerne la distribution de pression p. Nous constatons que 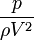p \over {\rho V^2} est sans dimension. Nous pouvons donc affirmer que: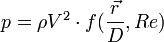

p = \rho V^2 \cdot f({\vec{r} \over D}, Re)

Nous pouvons appliquer le même raisonnement aux grandeurs ne dépendant pas des coordonnées. Par exemple, le force de résistance F s'exerçant sur le corps placé dans un écoulement de fluide. Nous pouvons alors dire que:

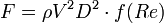
F = \rho V^2 D^2 \cdot f(Re)


Si la force de pesanteur affecte notablement le mouvement, celui-ci dépendra non plus de trois mais de quatre paramètres: D, V, ν et g. Nous pouvons alors former deux combinaisons: le nombre de Reynolds et le nombre de Froude défini par:

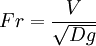
Fr = {V \over {\sqrt{D g}}}

Les fonctions f du nombre de Reynolds données précédemment dépendront alors de Re et Fr et les écoulements ne seront semblables que si ces deux nombres y sont égaux.


Pour un écoulement non permanent, il faudra ajouter la grandeur τ: intervalle de temps caractéristique au cours duquel cet écoulement varie. Nous pouvons alors former deux quantités sans dimensions: le nombre de Reynolds et le nombre de Strouhal défini par: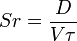

Sr = {D \over {V \tau}}

La similitude des écoulements implique alors l'égalité de chacun de ces nombres dans les deux écoulements.


Si on considère l'écoulement d'un fluide dont la caractéristique essentielle est la compressibilité, l'expérience montre que les deux seuls paramètres significatifs, en plus de la géométrie, sont la vitesse V de l'écoulement non perturbé et un paramètre lié à la compressibilité, le plus simple étant la célérité du son dans le fluide notée a. Ces deux grandeurs ayant la même dimension, le nombre sans dimension à conserver s'en déduit immédiatement, c'est le nombre de Mach:

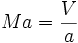
Ma = {V \over a}\,

Commentaire

Dans une expérience pratique, il est souvent impossible de satisfaire simultanément plusieurs conditions de similitude. Ainsi, lors du déplacement d'une maquette de navire, il faudrait en principe respecter la similitude de Reynolds pour décrire les frottements sur la coque et la similitude de Froude pour décrire le sillage sur la surface libre. Une inspection rapide des formules montre qu'une réduction de l'échelle devrait entraîner à la fois une réduction et une augmentation de la vitesse – sauf à pouvoir jouer sur la masse spécifique du fluide, sa viscosité ou la gravité. Dans ce cas il faut respecter la similitude la plus importante, généralement la similitude de Froude. Si les contraintes, essentiellement financières, permettent d'atteindre une échelle suffisamment grande pour que l'effet d'échelle lié au non-respect de la similitude de Reynolds soit faible, le problème est ignoré. Sinon, il faut appliquer aux résultats une correction numérique déduite d'autres expériences.

Interprétation des résultats d'essais

Dans ce qui précède, les nombres sans dimension sont considérés comme des marqueurs d'un phénomène bien déterminé : si l'un d'entre eux est modifié, les résultats doivent en principe changer. Quand des essais systématiques sont effectués pour obtenir des lois expérimentales, la présentation la plus efficace consiste à donner les résultats sous la forme d'une loi qui relie un nombre sans dimension à d'autres nombres sans dimension.

Une analyse plus approfondie peut même donner une idée sur la forme des lois à rechercher. Cette analyse peut s'appuyer sur le théorème de Buckingham mais une méthode plus élémentaire, due à lord Rayleigh, peut être utilisée dans les cas simples. On trouvera ci-dessous le canevas du calcul pour le problème classique de la force exercée sur un obstacle par l'écoulement d'un fluide que l'on supposera visqueux mais incompressible et sans surface libre. Les variables en cause, qui ne dépendent que de la masse M, de la longueur L et du temps T, sont

  • la force F de dimension MLT-2,
  • une dimension D caractéristique de l'obstacle, de dimension L,
  • l'incidence θ de l'écoulement par rapport à l'obstacle, qui ne dépend d'aucune des variables de base,
  • la vitesse V de l'écoulement, de dimension LT-1,
  • la masse spécifique ρ du fluide, de dimension ML-3,
  • sa viscosité μ de dimension ML-1T-1.

Il faut exprimer la force comme une fonction inconnue des autres variables :

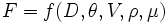
F = f(D,\theta,V,\rho,\mu)\,

Cette fonction peut être considérée comme une sorte de série contenant des monômes dans lesquels les différentes grandeurs sont élevées à des puissances inconnues multipliés par un coefficient k sans dimension :

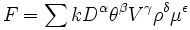
F = \sum k {D^\alpha \theta^\beta V^\gamma \rho^\delta \mu^\epsilon}

Une identification analogue à celle qui a été évoquée pour le nombre de Froude élimine trois des exposants et conduit à écrire la formule sous la forme :

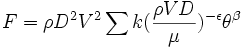
F =\rho D^2 V^2 \sum k ({{\rho V D} \over \mu})^{-\epsilon} \theta^\beta

qui contient deux paramètres indéterminés. La série se transforme en une fonction qui s'écrit sous la forme habituelle faisant intervenir une aire A caractéristique à la place du produit D2 :

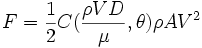
F = {1 \over 2} C({{\rho V D} \over \mu},\theta) \rho A V^2

Cette formule ne signifie pas que la force est proportionnelle au carré de la vitesse. En effet, celle-ci intervient à travers le nombre de Reynolds et, en d'autres circonstances, elle pourrait dépendre aussi du nombre de Mach et du nombre de Froude. Il existe des cas dans lesquels cette proportionnalité est bien vérifiée mais c'est une conséquence des expériences, pas de l'analyse dimensionnelle. Celle-ci ne peut qu'indiquer la forme la plus efficace pour décrire les lois physiques mais pas leur contenu.

Pour mettre en forme des résultats d'essais, cette formule s'écrit comme un nombre sans dimension fonction de deux autres nombres sans dimension :

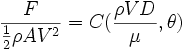
{F \over {{1 \over 2} \rho A V^2}} = C({{\rho V D} \over \mu},\theta)

Notes et références

  1. ↑ Site du Bureau international des mesures
  2. ↑
    • Bernard Stanford Massey, Measures in science and engineering : their expression, relation and interpretation, Halsted Press, 1986, 216 p. (ISBN 0853126070) 
    • (en) Carl W. Hall, Laws and Models: Science, Engineering, and Technology, CRC Press, 2000, 524 p. (ISBN 0849320186) 

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « Grandeur sans dimension ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de similitude de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Loi de similitude — ● Loi de similitude principe de base de la méthode homéopathique qui repose sur l analogie existant entre les symptômes exprimés par le malade et les signes pathologiques apparus chez l homme sain et sensible à qui l on a administré une substance …   Encyclopédie Universelle

  • loi de similitude — panašumo dėsnis statusas T sritis fizika atitikmenys: angl. similarity law; similarity principle; similitude law vok. Ähnlichkeitsgesetz, n; Ähnlichkeitssatz, m; Similaritätsprinzip, n rus. закон подобия, m; принцип подобия, m pranc. loi… …   Fizikos terminų žodynas

  • similitude — [ similityd ] n. f. • 1225; lat. similitudo 1 ♦ Relation unissant deux choses exactement semblables. ⇒ analogie, ressemblance. Similitude de goûts entre deux personnes. « Entre Faust et la Tentation il y a similitude d origines » (Valéry). ⇒… …   Encyclopédie Universelle

  • loi d’affinité — panašumo dėsnis statusas T sritis fizika atitikmenys: angl. similarity law; similarity principle; similitude law vok. Ähnlichkeitsgesetz, n; Ähnlichkeitssatz, m; Similaritätsprinzip, n rus. закон подобия, m; принцип подобия, m pranc. loi… …   Fizikos terminų žodynas

  • similitude law — panašumo dėsnis statusas T sritis fizika atitikmenys: angl. similarity law; similarity principle; similitude law vok. Ähnlichkeitsgesetz, n; Ähnlichkeitssatz, m; Similaritätsprinzip, n rus. закон подобия, m; принцип подобия, m pranc. loi… …   Fizikos terminų žodynas

  • Similitude directe — Similitude (géométrie) Pour les articles homonymes, voir Similitude. Les objets de même couleur sont semblables. En géométrie, u …   Wikipédia en Français

  • Loi Des Trois États — La loi des trois états est un concept énoncé par Auguste Comte, fondateur du positivisme, selon lequel l esprit humain passe par trois états successifs qui constituent les trois étapes de l espèce humaine (mais aussi de chaque individu) :… …   Wikipédia en Français

  • Loi des trois etats — Loi des trois états La loi des trois états est un concept énoncé par Auguste Comte, fondateur du positivisme, selon lequel l esprit humain passe par trois états successifs qui constituent les trois étapes de l espèce humaine (mais aussi de chaque …   Wikipédia en Français

  • Loi des « trois états » — Loi des trois états La loi des trois états est un concept énoncé par Auguste Comte, fondateur du positivisme, selon lequel l esprit humain passe par trois états successifs qui constituent les trois étapes de l espèce humaine (mais aussi de chaque …   Wikipédia en Français

  • Similitude (géométrie) — Pour les articles homonymes, voir Similitude. Pour la similitude des triangles, voir Triangles semblables. En géométrie euclidienne, une similitude est une transformation qui multiplie toutes les distances par une constante fixe, appelée son… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”