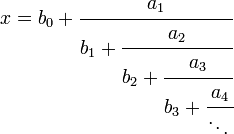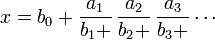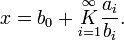Fractions continuées

Fraction continue

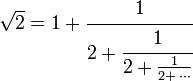
$\sqrt 2 = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \frac{1}{2+\,\cdots}}}$

Exemple de développement infini en fraction continue

En mathématiques, une fraction continue ou fraction continue simple ou encore fraction continuée^[1] est une expression de la forme :

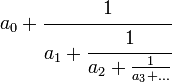
$a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\frac{1}{a_3+\dots}}}$

comportant un nombre fini ou infini d'étages. Une fraction continue généralisée est l'analogue d'une fraction continue, mais avec les 1 remplacés par des valeurs b_j :

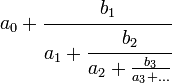
$a_0+\cfrac{b_1}{a_1+\cfrac{b_2}{a_2+\frac{b_3}{a_3+\dots}}}$

Le présent article porte principalement sur les fractions continues simples.

On montre qu'on peut représenter tout nombre réel sous forme d'une fraction continue, finie ou infinie, dans laquelle a₀ est un entier relatif et les a_j sont des entiers strictement positifs. Le sens du mot représenter sera précisé ultérieurement.

Comme dans la notation décimale usuelle, où chaque nombre réel est approché par des nombres décimaux de plus en plus précisément au fur et à mesure de la donnée des décimales successives, de même chaque nombre réel est approché par des fractions étagées de la forme ci-dessus de plus en plus précisément au fur et à mesure qu'on rajoute des étages. En outre, s'il faut une infinité de décimales pour décrire exactement un nombre non décimal, il faut un développement infini en fraction continue pour décrire exactement un nombre irrationnel.

Les fractions continues sont utiles en approximation diophantienne, notamment parce qu'elles fournissent, en un certain sens, les « meilleures » approximations des nombres réels par des nombres rationnels. Cette propriété est à l’origine d’algorithmes pour l’approximation de racines carrées, mais aussi de démonstrations d’irrationalité voire de transcendance pour certains nombres comme π ou e. La périodicité des fractions continues des racines carrées d’entiers strictement supérieurs à un et sans facteur carré a des conséquences utiles pour l’étude de l’équation de Pell-Fermat.

Déjà usitées chez les mathématiciens indiens au Moyen Âge, les fractions continues sont étudiées en Europe dès le XVII^e siècle et constituent encore un vaste sujet de recherche, près de 3 000 articles ont été publiés sur ce sujet au XX^e siècle. Elles sont maintenant généralisées à d'autres expressions, appliquées à l'approximation de séries entières appelées approximant de Padé ou encore adaptées aux applications linéaires.

Joseph-Louis Lagrange établit de manière rigoureuse les propriétés des fractions continues des entiers quadratiques.

Tour d'horizon

Henri Padé étudie le cas des fractions continues construites à l'aide de polynômes.

La notion de fraction continue est vaste et se retrouve dans de nombreuses branches des mathématiques. Les concepts associés peuvent aussi bien être relativement simples comme l'algorithme d'Euclide ou beaucoup plus subtils comme une fonction méromorphe^[2].

Il est possible, dans un premier temps, de voir une fraction continue comme une suite de nombres entiers qui représente un nombre réel. Cette situation est un peu la même que celle du système décimal qui représente π par la suite d'entiers 3, 1, 4, 1, 5, 9 ... Sous forme de fraction continue, la suite est 3, 7, 15, 292, 1, 1, ... Un premier champ d'étude consiste à étudier la relation entre la suite 3, 7, 15, 292, 1, 1, .... et celle des nombres rationnels que propose la fraction continue, en l'occurrence 3, 22/7, 333/106 etc, il permet de savoir comment passer de la première suite à la deuxième, comment la deuxième converge et répond à d'autres questions de cette nature. Tel est essentiellement l'objet de cet article.

Les fractions continues ont une relation particulière avec les racines carrées ou plus généralement les nombres, dits quadratiques, de la forme a + b.√d ou a et b sont des nombres rationnels et d un entier sans facteur carré. Les fractions continues associées sont périodiques, à partir d'un certain rang, c'est-à-dire que la suite des entiers formant la fraction continue se répète à partir d'un certain rang et jusqu'à l'infini^[3]. Cette situation est à l'image des représentations décimales infinies de nombres rationnels. Ces fractions continues permettent de résoudre un célèbre problème d'arithmétique appelé équation de Pell-Fermat^[4]. Cette question fait l'objet de l'article Fraction continue d'un nombre quadratique.

À l'image du système décimal, la fraction continue offre des nombres rationnels de plus en plus approchés de leur cible. Ces approximations sont bien meilleures que celles décimales. La deuxième approximation décimale de π, égale à 31/10 possède un dénominateur relativement proche de celui de la deuxième approximation de la fraction continue 22/7, en revanche 22/7 est plus de 30 fois plus précis que 31/10. Ce type d'approche d'un nombre réel par un nombre rationnel est appelé approximation diophantienne. Les fractions continues y jouent un grand rôle. Elles ont permis de construire le premier nombre transcendant connu^[5] ou de montrer que e la base du logarithme népérien est irrationnel^[6]. À condition de généraliser la définition d'une fraction continue, il devient possible de montrer que π est aussi irrationnel puis que ces deux derniers nombres sont transcendants^[7]. Cette approche est traitée dans l'article Fraction continue et approximation diophantienne.

Une fraction continue ne concerne pas uniquement les nombres mais aussi les fonctions. On construit des fractions continues généralisées en remplaçant les coefficients a_n et b_n par des polynômes^[8]. Une motivation provient de l'analyse complexe, qui a pour objet l'étude des fonctions de la variable complexe à valeur complexe, ayant une bonne propriété de régularité appelée dérivabilité. L'approche classique consiste à construire une suite de polynômes de degré de plus en plus élevé, appelée série entière, et qui converge vers la fonction cible. Une spécificité fréquente, pour ce type de fonction est de posséder des pôles, c'est-à-dire des espèces de montagnes qui grimpent jusqu'à l'infini. Sa série entière ne permet pas de voir plus loin qu'un pôle. Si, au lieu d'approcher la fonction par des polynômes, on utilise des quotients, on construit des fractions continues appelées approximants de Padé^[9]. Elles possèdent le mérite de permettre de voir l'autre versant des pôles.

D'autres propriétés ont été étudiées. À la différence du système décimal, un entier apparaissant dans une fraction continue n'est en général pas borné par 9, il peut devenir arbitrairement grand. Alexandre Khintchine s'est intéressé à la moyenne, au sens de limite des moyennes géométriques de tous ces dénominateurs. Pour presque tous les nombres, cette moyenne est la même^[10]. Le mot presque possède ici un sens bien particulier. Cette moyenne est appelée constante de Khintchine.

Il est aussi possible de construire des développements en fractions en plaçant les barres de fraction sur le numérateur et non en dessous, on obtient un développement en série d'Engel^[11] :

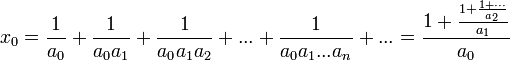
$x_0 = \frac{1}{a_0} + \frac{1}{a_0a_1} + \frac{1}{a_0a_1a_2}+ ... + \frac{1}{a_0a_1...a_n} + ...= \frac{1 + \frac{1+ \frac{1+ \cdots}{a_2}}{a_1}}{a_0}$

Approche intuitive

De l’algorithme d’Euclide aux fractions continues

Article détaillé : Algorithme d'Euclide.

On commence par rappeler le déroulement de l'algorithme dû à Euclide de recherche du PGCD, en analysant l'exemple des deux nombres entiers 15 625 et 6 842. On procède à une suite de divisions euclidiennes avec reste :

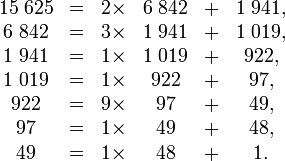
$\begin{matrix} 15\;625 &= &2 \times &6\;842 &+&1\;941,&\\ 6\;842 &= &3 \times &1\;941 &+&1\;019,&\\ 1\;941 &= &1 \times &1\;019 &+&922,&\\ 1\;019 &= &1 \times &922 &+&97,&\\ 922 &= &9 \times &97 &+&49,&\\ 97 &= &1 \times &49 &+&48,&\\ 49 &=&1 \times &48 &+&1.& \end{matrix}$

Une autre manière d'interpréter cet algorithme consiste à approcher par étapes le quotient 15 625 / 6 842. La partie entière de ce quotient est 2, ce qui permet d'écrire

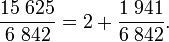
$\frac{15\;625}{6\;842}=2+\frac{1\;941}{6\;842}.$

Que peut-on dire de la fraction 1 941 /6 842, à part qu'elle est plus petite que 1? Elle est comprise entre 1/4 et 1/3, son inverse, 6 842 / 1 941, possède une partie entière est 3 ; et plus précisément, si l'on utilise les résultats de la deuxième division euclidienne :

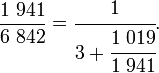
$\frac{1\;941}{6\;842}=\cfrac{1}{3+\cfrac{1\;019}{1\;941}}.$

Ainsi de proche en proche :

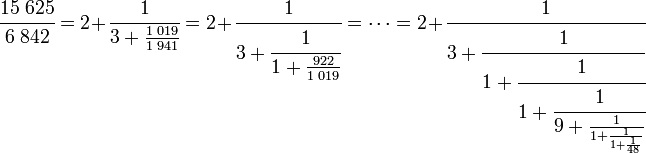
$\cfrac{15\;625}{6\;842}=2+\cfrac{1}{3+\frac{1\;019}{1\;941}}=2+\cfrac{1}{3+\cfrac{1}{1+\frac{922}{1\;019}}}=\dots= 2+\cfrac{1}{3+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{9+\frac{1}{1+\frac{1}{1+\frac{1}{48}}}}}}}$

qui est bien une fraction continue. On utilise parfois la notation suivante, plus commode :

$\frac{15\;625}{6\;842}=[2,3,1,1,9,1,1,48].$

On peut comparer 15 625 / 6 842 à ses approximants obtenus en tronquant successivement le nombre d'étages de la fraction continue. Le tableau suivant donne les troncatures en notation fractionnelle puis décimale, et la différence entre l'approximant et le nombre 15 625 / 6 842.

Approximants successifs de 15 625 / 6 842 et évolution de l'erreur

Fraction	Développement décimal	Erreur
2	2,0000...	-0,283 688 979 83...
7/3 = 2 + 1/3	2,333...	0,049 644 353 5...
9/4 = 2 + 1/(3 + 1/1)	2,250 0...	-0,033 688 897 983...
16/7	2,285 714 285 714 2...	0,002 025 305 88...
153/67	2,283 582 089 55...	-0,000 106 890 28...
169/74	2,283 783 783 7......	0,00009480395...
322/141	2,283 687 943 2	-0,000 001 036 57...
15 625/6 842	2,283 688 979 83...	0

La suite des erreurs est décroissante en valeur absolue et de signes alternés.

Développement en fraction continue d'un rationnel

On peut chercher si tout nombre rationnel r admet un développement en fraction continue. Soit donc r = p / q une de ses représentations fractionnaires. On cherche, s'il existe, un nombre positif ou nul n, un entier relatif a₀ et des entiers strictement positifs a_j pour j ≥ 1, tels que r = [a₀, ...,a_n]. Sans perte de généralité, on peut supposer q > 0, et introduire les nombres p₀, p₁,... et a₀, a₁, ... comme suit.

On pose p₀ = p , p₁ = q

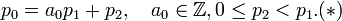
$p_0=a_0p_1+p_2, \quad a_0\in \mathbb{Z}, 0\le p_2<p_1. (*)$

C'est une division euclidienne ordinaire si p₀ est positif ou nul. S'il est strictement négatif, on a -p₀ = a'₀.p₁ + p'₂ avec a'₀ entier positif ou nul, 0 ≤ p'₂ < p₁. Si p'₂ est nul, on pose a₀ = a'₀ et p₂ = 0, et s'il n'est pas nul, on pose a₀ = -a'₀ - 1 et p₂ = p₁ - p'₂. Dans ces deux cas, on obtient encore (*). Tant que p_j n'est pas nul, on pose

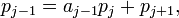
$p_{j-1}=a_{j-1}p_j +p_{j+1},\;$

avec a_j-1 entier au moins égal à 1(pour j >1) et 0 ≤ p_j+1 < p_j. On note n le plus grand entier pour lequel p_n+1 n'est pas nul. On sait donc que p_n+1/p_n est un entier supérieur à 1. On a alors

$\frac{p_0}{p_1}=[a_0,p_1/p_2]=[a_0,a_1,p_2/p_3]=\dots=[a_0,a_1,\dots,a_n].$

On peut vérifier que :

$[a_n]=p_n/p_{n+1},\quad [a_{n-1},a_n]=a_{n-1}+p_{n+1}/p_n=p_{n-1}/p_n,[a_j,\dots,a_n]=a_j+p_{j+2}/p_{j+1}=p_j/p_{j+1}$

et une récurrence immédiate montre [a₀, ...,a_n] = p / q.

On a donc montré que l'algorithme du PGCD d'Euclide fournit systématiquement un développement en fraction continue d'un nombre rationnel. Le développement ainsi obtenu est toujours fini.

Les numérateurs et dénominateurs des différentes réduites s'obtiennent par l'algorithme d'Euclide étendu.

On peut se demander s'il y a d'autres développements finis d'un rationnel en fraction continue. On remarque d'abord que pour tout entier relatif m, [m-1, 1] est identique à m. Par conséquent, si r admet le développement en fraction continue [a₀, ..., a_n] avec a_n > 1 , il admet aussi le développement [a₀, ..., a_n - 1, 1]. Un raisonnement simple par récurrence montre qu'il ne peut y avoir d'autres développements en fraction continue que ceux qui viennent d'être donnés. Enfin, on peut montrer que tout rationnel possède un développement en fraction continue fini.

Le nombre x possède une représentation en fraction continue finie si et seulement si, x est un nombre rationnel — démonstration

On sait déjà que si x possède un développement fini en fraction continue, il est rationnel.

Réciproquement montrons que si x est rationnel, il admet un développement fini en fraction continue. Soit p et q deux entiers tels que x soit égal à p / q. Ici q désigne un entier strictement positif. Montrons par récurrence sur q que x admet une représentation finie.

Si q est égal à 1, alors x est égal à p, ce qui fournit une représentation en fraction rationnelle finie.

Supposons la propriété vérifiée pour toutes les fractions admettant un dénominateur strictement plus petit que q. La division euclidienne de p par q montre l'existence de deux entiers d et r tels que :

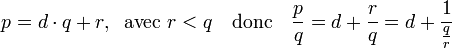
$p = d\cdot q + r,\;\text{ avec } r< q \quad\text{donc}\quad \frac pq = d + \frac rq = d + \frac 1{\frac qr}\;$

L'hypothèse de récurrence montre que la fraction q / r admet un développement fini en fraction continue. Le remplacement de la valeur q / r dans l'expression précédente fournit un développement fini en fraction continue de p/q ce qui termine la démonstration.

Développement en fraction continue du nombre π

Une remarque permet de généraliser la méthode précédente à un nombre réel quelconque. Pour l'illustrer, appliquons là sur le nombre π. La première étape, dans le cas d'un rationnel, était le calcul de la division euclidienne du numérateur par le dénominateur, ce qui ne fait plus sens pour un réel, en revanche le résultat est égal à la partie entière de la fraction, qui possède toujours un sens. La partie fractionnaire, nécessairement plus petite que 1, était inversée, ce qui est encore possible ici. On obtient :

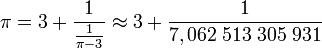
$\pi = 3 + \frac 1{\frac 1{\pi-3}}\approx 3 + \frac 1{7,062\;513\;305\;931}$

Comme π est irrationnel, l'inverse de π - 3 l'est encore, l'algorithme ne s'arrète pas. Comme π - 3 est plus petit que 1, c'est une partie fractionnaire, son inverse est plus grand que 1 et l'on peut appliquer la même démarche :

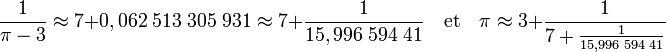
$\frac 1{\pi-3} \approx 7 + 0,062\;513\;305\;931 \approx 7 + \frac 1{15,996\;594\;41}\quad\text{et}\quad \pi \approx 3 + \frac 1{7+\frac 1{15,996\;594\;41}}$

Le nouvelle valeur approximativement égale à 15,997 est encore un irrationnel strictement supérieur à 1, d'où la possibilité d'une nouvelle étape, puis d'une nouvelle :

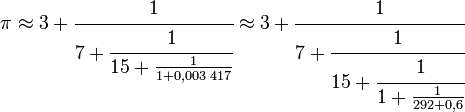
$\pi \approx 3+ \cfrac 1{7+\cfrac 1{15 + \frac 1{1 + 0,003\;417}}} \approx 3+ \cfrac 1{7+\cfrac 1{15 + \cfrac 1{1 + \frac 1{292 + 0,6}}}}$

On comprend que le processus ne s'arrête jamais, si le calcul est réalisé avec un nombre de décimales suffisant. On obtient comme suite de fractions 3 puis 22/7 ≈ 3,1428 puis 333/106 ≈ 3,14150 puis 355/113 ≈ 3,1415929 et enfin 103 993 / 331 02 proche de π avec une précision meilleure que le milliardième. Une fois encore, la suite des erreurs est décroissante en valeur absolue et de signes alternés.

Représentation géométrique

Un pavage d'un rectangle de longueur 30 et de largeur 13 permet de déterminer l'expression de 30/13 en fraction continue : 30/13=[2 , 3, 4]

L'algorithme d'Euclide permet de calculer une fraction continue dans le cas des nombres rationnels. Cet algorithme admet dans ce cadre une interprétation géométrique. Soit r = p / q un nombre rationnel, on considère un rectangle de longueur p et de largeur q, et on le pave par des carrés de côté q.

Si x est un nombre entier, le pavage comporte exactement x carrés. Sinon, soit a₀ le nombre de carrés insérés dans le rectangle, ou encore, le premier terme de la fraction continue. Il reste une bande non pavée de dimension q x b₁ avec b₁ égal à p - a₀.q ; on pave cette bande avec des carrés de dimension maximale, c'est-à-dire de côté x₁. Le nombre de carrés est égal au deuxième terme a₁ de la fraction continue. En réitérant la méthode, on obtient l'intégralité des coefficients a_p.

Dans l'image ci-contre, on pave le rectangle 30 x 13 par deux carrés de côtés 13. Il reste une bande de longueur 13 et de largeur 4. En termes de fraction continue, on obtient l'égalité :

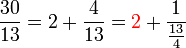
$\frac {30}{13} = 2 + \frac 4{13} = {\color{Red}2} + \frac 1{\frac {13}4}\;$

La même démarche s'applique pour déterminer un rationnel connaissant sa fraction continue. [1 , 1 , 2 , 3] = 17/10

Ensuite, on remarque qu'il est possible de remplir la bande restante de 3 carrés de côté 4 et il reste une bande de longueur 4 et de largeur 1. Ce qui permet de terminer le calcul de la fraction continue :

$13 = 3\times4 + 1 \;\Rightarrow \; \frac {30}{13} = {\color{Red}2} + \frac 1{\frac {3\times 4 + 1 }4} = {\color{Red}2} + \frac 1{{\color{Red}3} + \frac 1{\color{Red}4}}= [2,3,4]\;$

La technique du pavage conduit à une fraction continue infinie si la longueur et largeur du rectangle est incommensurable.

La même construction permet de trouver le rationnel dont on connait le développement en fraction continue. Dans l'image de gauche on peut retrouver le rationnel dont le développement est [1, 1, 2, 3]. Le dernier coefficient est égal à 3, on trouve donc 3 petits carrés de côté 1, qui donnent la taille du carré suivant (3). L'avant dernier coefficient 2 indique qu'il existe deux carrés moyens de côté 3. Ces deux cotés et le petit carré donnent la taille du carré plus grand (7). Le coefficient associé est égal à 1, il n'en n'existe donc qu'un unique de cette nature. Le carré plus grand (7) et le carré moyen (3) donnent le coté du dernier carré (10). Les deux derniers carrés donnent la longueur totale du rectangle (17). La fraction recherchée est égale à 17/10.

Le processus s'arrête car p et q sont commensurables c'est-à-dire qu'il existe une longueur l et deux entiers a et b tels que p = l.a et q = l.b.

Considérons maintenant un rectangle de longueur L et de largeur l. Si le quotient L / l n'est pas rationnel, c'est-à-dire si les longueurs L et l sont incommensurables, le processus ne s'arrête pas.

Tel est le cas pour la figure de droite représentant un rectangle d'or, c'est-à-dire un rectangle dont le rapport de la longueur sur la largeur est égal à φ le nombre d'or. On ne peut placer qu'un carré dans chaque bande ce qui amène à la représentation :

$\varphi = [1 , 1 , 1 , \cdots]$

La suite des numérateurs, ainsi que celle des dénominateurs sont de Fibonacci.

Repère chronologique

Âryabhata, un mathématicien indien, fait usage des fractions continues dès le V^e siècle.

L'usage des fractions continues est ancien. Âryabhata (476 - 550), un mathématicien indien les utilise pour résoudre des équations diophantiennes ainsi que pour approximer précisément des nombres irrationnels^[12]. Brahmagupta (598 – 668) étudie plus en profondeur l'équation maintenant dite de Pell-Fermat. Il développe les premiers fondements de la méthode chakravala, usant de calculs proches de ceux des fractions continues^[13]. Il cherche à résoudre l'équation x² - 61. y² = 1 et trouve la plus petite solution :

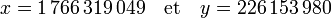
$x= 1\, 766 \, 319 \, 049\quad \text{et}\quad y = 226\, 153\, 980$

Au XII^e siècle, la méthode est enrichie par Bhāskara II. Un algorithme, analogue à celui des fractions continues, permet de résoudre un cas général. La différence la plus marquante est qu'il autorise les nombres négatifs dans la fraction, permettant une convergence plus rapide^[14].

L'apparition en Europe est plus tardive et italienne. Rafael Bombelli (1526 – 1572) fait usage d'un ancêtre des fractions continues pour le calcul d'approximations de la racine carrée de 13^[15]. Pietro Antonio Cataldi (1548 – 1626) comprend que la méthode de Bombelli s'applique pour toutes les racines carrées, il l'utilise pour la valeur 18 et écrit un petit opuscule à ce sujet^[16]. Il remarque que les approximations obtenues sont alternativement supérieures et inférieures à la racine carrée cherchée.

John Wallis, à la suite des travaux de William Brouncker, utilise pour la première fois l'expression de fraction continue.

Un progrès décisif a lieu en Angleterre. Le 3 janvier 1657, Pierre de Fermat défie les mathématiciens européens avec plusieurs questions dont l'équation déjà résolue par Brahmagupta^[17]. Piqué au vif^[18], la réaction anglaise est rapide. William Brouncker (1620 – 1684) trouve la relation entre l'équation et la fraction continue, ainsi qu'une méthode algorithmique équivalente à celle des indiens pour le calcul de la solution. Il utilise la fraction continue pour construire une suite convergente vers 4/π, et approxime π avec dix décimales significatives^[19]. Ces résultats sont publiés par John Wallis qui en profite pour démontrer les relations de récurrence utilisées par Brouncker et Bhāskara II. Il donne le nom de fraction continue dans la phrase : « Nempe si unitati adjungatur fractio, quae denominatorem habeat continue fractum. »^[20]. À cette époque, Christiaan Huygens (1629 – 1695) découvre que les fractions continues sont l'outil idéal pour déterminer le nombre de dents que doivent contenir les roues des engrenages dans l'horlogerie. Il l'utilise pour la mise au point d'un automate planétaire^[21].

Quelques questions théoriques sont résolues au siècle suivant. L'usage montre que l'algorithme des fractions continues permet de résoudre l'équation de Pell-Fermat en utilisant le fait que la fraction est périodique à partir d'un certain rang. Leonhard Euler (1707 – 1783) montre que si un nombre possède une fraction continue périodique, alors il est solution d'une équation du second degré à coefficients entiers^[22]. La réciproque, plus subtile^[23] est l'œuvre de Joseph-Louis Lagrange (1736 - 1813). Durant ce siècle, Johann Heinrich Lambert (1728 – 1777) trouve une nouvelle utilité aux fractions continues. Il les utilise pour montrer l'irrationalité de π.

Cet usage devient fréquent au XIX^e siècle. Evariste Galois (1811 - 1832) trouve la condition nécessaire et suffisante pour qu'une fraction continue soit immédiatement périodique^[24]. Joseph Liouville (1809 - 1882) utilise le développement en fraction continue généralisée pour exhiber des nombres non algébriques, c’est-à-dire transcendants. Ce sont les nombres de Liouville. En utilisant les fractions continues, Charles Hermite (1822 - 1901) prouve^[25] la transcendance de e, base du logarithme népérien en 1873. Grâce à lui, Ferdinand von Lindemann prouve en 1882 que π est transcendant et démontre par la même que la quadrature du cercle est impossible à réaliser. À la fin du siècle Henri Padé (1863 - 1953) développe la théorie^[26] des approximants qui portent maintenant son nom et qui sont des fractions continues de polynômes. Cette technique est utilisée par Henri Poincaré (1854-1912) pour démontrer la statibilité du système solaire^[27]. Georg Cantor (1845 - 1918) prouve que les points d'un segment et ceux situés à l'intérieur d'un carré sont en bijection à l'aide des fractions continues^[28]. Les fonctions de cette nature sont étudiées dans le cadre de la théorie du chaos, elles sont discontinues sur chaque point rationnel de l'intervalle [0,1]^[29].

Approche théorique

Algorithme de développement en fraction continue pour un réel

Dans l'algorithme d'Euclide développé précédemment, l'entier a_j, quotient de p_j dans la division euclidienne par p_j+1 est aussi la partie entière du réel x_j défini par p_j/p_j+1. Le réel p_j+2/p_j+1 représente la partie décimale de x_j et peut encore s'écrire x_j - a_j. Le réel x_j+1 défini par p_j+1/p_j+2 correspond donc à 1/(x_j - a_j).

À l'aide des idées introduites précédemment, on peut alors définir un développement en fraction continue pour tout réel x . Le symbole 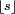$\scriptstyle{\lfloor s\rfloor}$ désigne la partie entière du nombre s. On pose :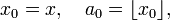

$x_0=x,\quad a_0=\lfloor x_0\rfloor,$

ainsi que la définition récurrente, tant que x_j n'est pas entier,

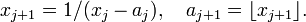
$x_{j+1}=1/(x_j-a_j),\quad a_{j+1}=\lfloor x_{j+1}\rfloor.$

L'entier n désigne, s'il existe, le premier indice pour lequel x_j est entier, on définit alors a_n comme étant égal à x_n. Le développement obtenu par le présent algorithme est alors fini. Sinon, il ne s'arrête jamais.

On peut formaliser de manière plus informatique cet algorithme :

Donnée : un nombre x réel.
Initialisation : on assigne la valeur x à la variable X. La suite a est vide.
Boucle: On assigne à la variable A le plus grand entier au plus égal à X, on concatène cette valeur à la suite a. Si X est entier, l'algorithme s'arrête. Si X n'est pas entier, on assigne à X la valeur de 1 /(X - A) et on recommence au début de la boucle.

On sait que cet algorithme s'arrête si et seulement si x est rationnel.

Notations et terminologie

Pour des nombres a_j, j ≥ 0, qu'on peut aussi voir comme des variables formelles, on introduit les expressions suivantes:

$[a_0]=a_0,\quad [a_0,a_1]=a_0+\frac{1}{a_1},\quad \dots [a_0,\dots,a_j] =a_0+\frac{1}{[a_1,\dots,a_j]},$

quel que soit l'entier positif j. Si a₀ est un entier relatif, et si a₁,... , a_p sont des entiers strictement positifs, l'expression [a₀,... , a_p] est bien définie et fournit un nombre rationnel.

Si x est un nombre réel, il est possible de définir les suites (a_j) et (x_j) à l'aide de la méthode du paragraphe précédent.

La suite (a_p) est appelée fraction continue ou fraction continue simple du réel x.

Si x est rationnel, la suite s'arrête pour un indice n, sinon elle est infinie.

L'usage des deux mots dépend du contexte. Dans certains cas, la majorité des expressions sont du type étudié jusqu'à présent. Pour plus de simplicité on parle de fraction continue. Les expressions différentes, par exemple parce que a_n devient négatif ou réel quelconque, sont appelées fractions continues généralisées. Dans d'autres situations, l'expression générale n'est pas celle où a_n est un entier, il peut être par exemple, une fonction complexe ou une matrice, le terme de fraction continue désigne alors l'objet mathématique principal étudié et les fractions dont il est question ici prennent le nom de fraction continue simple.

Le terme a_p est appelé coefficient d'indice p.

La fraction [a₀, a₁, a₂, ..., a_p] est appelée réduite ou encore quotient incomplet d'indice p.

Le terme x_p est appelé quotient complet d'indice p.

Deux notations sont fréquemment utilisées dans ce contexte :

$x = a_0 + \cfrac 1{a_1 + \cfrac 1{a_2 + \frac 1{\cdots}}} = [a_0, a_1, a_2, \cdots]$

Ces notations seraient abusives si la suite des réduites n'étaient pas convergente vers x, ce qui n'a été vérifié que pour les rationnels. Le reste de l'article montre que cette convergence existe toujours, ce qui justifie la notation.

Réduites d'une fraction continue

Dans le reste de la section, x est un réel, (a_p) sa fraction continue et (x_p) la suite associée à x selon les notations du premier paragraphe de la section. La lettre n désigne l'indice du dernier terme de la suite (a_p) si x est rationnel, et désigne l'infini si x est irrationnel. Enfin p désigne un entier positif ou nul, inférieur ou égal à n.

Par définition de la fraction continue, on dispose de l'égalité :

$x = [a_0, a_1, \cdots, a_{p-1}, x_p]$

Si p est strictement positif alors x_p est un réel supérieur à 1, et a_p est un entier strictement positif.

Ceci provient de la définition de x_p comme inverse de partie fractionnaire d'un nombre, et de la définition de a_p comme partie entière de x_p.

Si un nombre réel strictement positif x admet un développement en fraction continue de la forme [a₀,a₁,...], alors, son inverse 1/x admet pour développement en fraction continue [a₁,a₂,...] dans le cas où a₀ est nul, et [0,a₀,a₁,...] dans les autres cas.

Soit (h_p) et (k_p) les suites d'entiers (qui sont strictement positifs à partir du rang 1), définies par récurrence par : .

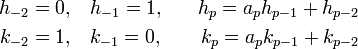
$\begin{align} h_{-2} = 0,\quad & h_{-1} = 1,\quad & h_p = a_ph_{p-1}+h_{p-2} \\ k_{-2} = 1,\quad & k_{-1} = 0,\quad & k_p = a_pk_{p-1}+k_{p-2}\end{align}$

Alors on a les trois propriétés suivantes :

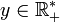Pour tout $y \in \mathbb R_+^*$ :

$\quad \left[a_0, a_1, \,\dots, a_{p-1}, y \right]= \frac{y h_{p-1}+h_{p-2}} {y k_{p-1}+k_{p-2}}$

L'égalité suivante est vérifiée :

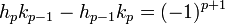
$h_pk_{p-1}-h_{p-1}k_p=(-1)^{p+1}\,$

L'écriture irréductible de la réduite d'ordre p est

$[a_0,a_1,\cdots a_p]=\frac{h_p}{k_p}$

Irréductible signifie que le numérateur et le dénominateur sont deux entiers premiers entre eux.

Si les coefficients de la fraction continue sont tous égaux à 1 - ce qui est le cas dans le développement en fractions continues du nombre d'or - les entiers h_p et k_p vérifient la relation de récurrence de Fibonacci, ce sont des nombres de Fibonacci consécutifs, ce qui explique que les quotients de deux termes consécutifs de la suite de Fibonacci donnent des approximations de plus en plus fines du nombre d'or.^[30]

Démonstrations

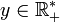Pour tout $y \in \mathbb R_+^*$ :

$\quad \left[a_0, a_1, \,\dots, a_{p-1}, y \right]= \frac{y h_{p-1}+h_{p-2}} {y k_{p-1}+k_{p-2}}$

Montrons cette propriété par récurrence sur p.

Lorsque p est nul les deux membres de l'identité valent y : elle est donc vérifiée.

Soit p un entier positif ou nul ; supposons la propriété vraie à l'ordre p . Elle est en particulier vraie lorsque y prend la valeur a_p + 1/y, ce qui permet d'écrire :

$\begin{array} {rl}[a_0,\cdots, a_p, y] &= [a_0,\cdots, a_{p-1}, a_p + \frac 1y]\\ & = \frac {(a_p + \frac 1y)h_{p-1} + h_{p-2}}{(a_p + \frac 1y)k_{p-1} + k_{p-2}}\\ & = \frac {y(a_ph_{p-1} + h_{p-2}) + h_{p-1}}{y(a_pk_{p-1} + k_{p-2}) + k_{p-1}}\\ & =\frac{y h_{p}+h_{p-1}} {y k_{p}+k_{p-1}} \end{array}$

En posant y = a_p, dans l'égalité précédente, on peut écrire

$\begin{array} {rl}[a_0,\cdots, a_{p-1}, a_p] &= \frac{a_p h_{p-1}+h_{p-2}} {a_p k_{p-1}+k_{p-1}}\\ & =\frac{h_p}{k_p} \end{array}$

L'égalité suivante est vérifiée :

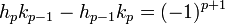
$h_pk_{p-1}-h_{p-1}k_p=(-1)^{p+1}\,$

Montrons cette égalité par récurrence sur p.

Lorsque p est nul les deux membres de l'égalité valent -1 ; elle est donc vérifiée.

Soit p un entier positif ou nul ; supposons vérifiée cette égalité à l'ordre p et vérifions la à l'ordre p+1. On calcule alors :

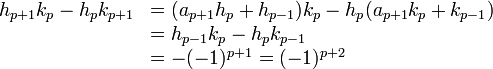
$\begin{array} {rl} h_{p+1}k_p-h_pk_{p+1} & = (a_{p+1}h_p + h_{p-1})k_p - h_p(a_{p+1}k_p + k_{p-1})\\ & = h_{p-1}k_p-h_pk_{p-1}\\ & = -(-1)^{p+1} = (-1)^{p+2} \end{array}$

La dernière égalité prouve que les entiers h_p et k_p sont premiers entre eux et que l'écriture de la réduite est bien une fraction irréductible.

Encadrement et convergence

La valeur x désigne maintenant un nombre irrationnel strictement positif. La suite (a_p) est infinie et ne prend que des valeurs positives.

Les deux suites (h_p) et (k_p) sont strictement croissantes et ont pour limite l'infini.

En effet, cette proposition est la conséquence directe de la relation de récurrence établie au paragraphe précédent. Une récurrence montre que la valeur de k_p est au moins égale à 2^p/2.

La suite des réduites est convergente, quelques propositions montrent la nature de cette convergence :

La différence entre deux réduites successives est :

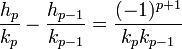
$\frac{h_p}{k_p}-\frac{h_{p-1}}{k_{p-1}} = \frac{(-1)^{p+1}}{k_pk_{p-1}}$

Les réduites de rangs pairs et impairs sont respectivement croissante et décroissante et définissent deux suites adjacentes convergeant vers x .

Ce résultat s'exprime aussi sous la forme suivante :

La valeur x est la limite de la série alternée :

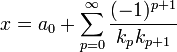
$x = a_0 + \sum_{p=0}^{\infty}\frac{(-1)^{p+1}}{k_pk_{p+1}}$

Si (a_p) est une suite d'entiers strictement positifs et (s_p) la réduite[a₀, ...,a_p] est la p^ième somme partielle de la série précédente qui est convergente. Si x désigne la limite de la série, alors la fraction continue de x est donnée par [a₀, ...,a_p, ...]. Ainsi, toute suite d'entiers strictement positifs, sauf peut être le premier, correspond au développement en fraction continue d'un réel.

La différence entre x et une réduite est évaluée par les formules suivantes :

Pour tout entier p, la différence entre la valeur x et la réduite d'indice p est donnée par la formule suivante, si x_p+1 désigne le quotient complet d'indice p + 1 :

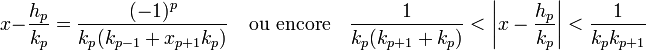
$x - \frac{h_p}{k_p}= \frac{(-1)^p}{k_p(k_{p-1} + x_{p+1}k_p)}\quad\text{ou encore}\quad \frac{1}{k_p(k_{p+1}+k_p)}<\left|x-\frac{h_p}{k_p}\right|<\frac{1}{k_pk_{p+1}}$

Ce qui montre que la limite d'une fraction continue est bien la valeur du nombre x initial. De plus, deux fractions continues de même limite ont nécessairement les mêmes coefficients. Soit en effet deux fractions continues ayant même limite x, montrons par récurrence que leur p premiers coefficients sont égaux. Si a₀ et la partie entière de x alors les deux fractions continues ont pour premier coefficient a₀. Supposons la propriété démontrée pour les p premiers coefficients. Le même raisonnement montre qu'ils ont même quotient complet d'ordre 1, les coefficients d'indice 1 à p des deux fractions continues correspondent aux p premiers coefficients de la fraction continue du quotient complet, ils sont donc égaux, de plus les deux fractions continues ont même coefficient d'ordre a₀. Les fractions ont donc les mêmes p + 1 premiers coefficients.^[30]

Démonstrations

La différence entre deux réduites successives est :

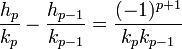
$\frac{h_p}{k_p}-\frac{h_{p-1}}{k_{p-1}} = \frac{(-1)^{p+1}}{k_pk_{p-1}}$

C'est une conséquence de la dernière des propriétés du paragraphe précédent :

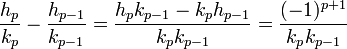
$\frac{h_p}{k_p}-\frac{h_{p-1}}{k_{p-1}} = \frac{h_pk_{p-1}-k_ph_{p-1}}{k_pk_{p-1}} = \frac{(-1)^{p+1}}{k_pk_{p-1}}$

Les réduites de rangs pairs et impairs définissent deux suites adjacentes convergeant vers x :

La formule précédente permet de calculer h_p+2/k_p+2 - h_p/k_p.

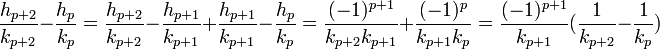
$\frac{h_{p+2}}{k_{p+2}}-\frac{h_{p}}{k_{p}}= \frac{h_{p+2}}{k_{p+2}}-\frac{h_{p+1}}{k_{p+1}}+\frac{h_{p+1}}{k_{p+1}}-\frac{h_p}{k_p}= \frac{(-1)^{p+1}}{k_{p+2}k_{p+1}} + \frac{(-1)^{p}}{k_{p+1}k_{p}} = \frac{(-1)^{p+1}}{k_{p+1}}(\frac{1}{k_{p+2}}-\frac{1}{k_p})$

On en déduit que la suite des réduites de rangs pairs est croissante et celle des réduites de rangs impairs décroissante. L'écart entre deux termes consécutifs est inférieur à 2^-p. Ceci démontre que les suites sont adjacentes.

La valeur x est la limite de la série alternée :

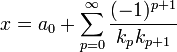
$x = a_0 + \sum_{p=0}^{\infty}\frac{(-1)^{p+1}}{k_pk_{p+1}}$

La valeur x est la limite de la suite (h_p/k_p), qui s'écrit encore :

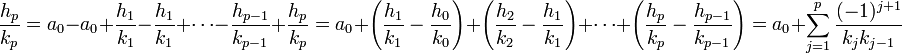
$\frac {h_p}{k_p}= a_0 -a_0 + \frac{h_1}{k_1} - \frac{h_1}{k_1} + \cdots - \frac{h_{p-1}}{k_{p-1}} + \frac{h_p}{k_p} = a_0 +\left(\frac{h_1}{k_1}- \frac{h_0}{k_0}\right) + \left(\frac{h_2}{k_2} - \frac{h_1}{k_1}\right) + \cdots + \left(\frac{h_p}{k_p} - \frac{h_{p-1}}{k_{p-1}}\right) = a_0 + \sum_{j=1}^p\frac{(-1)^{j+1}}{k_jk_{j-1}}$

Un passage à la limite sur p montre le résultat voulu.

Pour tout entier p, la différence entre x et la réduite de rang p est donnée par la formule suivante :

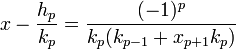
$x - \frac{h_p}{k_p}= \frac{(-1)^p}{k_p(k_{p-1} + x_{p+1}k_p)}$

L'expression du réel x en fonction des premiers coefficients de son développement en fraction continue et d'un quotient complet permet d'obtenir :

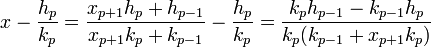
$x - \frac{h_p}{k_p}= \frac {x_{p+1}h_p + h_{p-1}}{x_{p+1}k_p + k_{p-1}} - \frac {h_p}{k_p} = \frac {k_ph_{p-1}-k_{p-1}h_p}{k_p(k_{p-1} + x_{p+1}k_p)}$

La dernière proposition du paragraphe précédent permet de conclure.

Les majorations suivantes sont vérifiées :

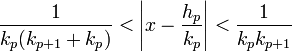
$\frac{1}{k_p(k_{p+1}+k_p)}<\left|x-\frac{h_p}{k_p}\right|<\frac{1}{k_pk_{p+1}}$

Il suffit de remarquer que x_p+1 est plus grand que 1 pour la majoration de gauche. Pour celle de droite, il suffit de remarquer que x_p+1 est plus grand que a_p+1 et que a_p+1.k_p - k_p-1 est égal à k_p+1.

Usages

Les usages des fractions continues sont innombrables. On trouvera par exemple dans Fraction continue et approximation diophantienne les preuves de l'irrationalité de e ou de π, dans Fraction continue d'un nombre quadratique un exemple de résolution d'équation de Pell-Fermat ou dans approximant de Padé un prolongement analytique de la série entière de la fonction tangente. Les usages donnés ici ne nécessitent pour leur compréhension que les propriétés décrites dans cet article.

Équation diophantienne linéaire

Article détaillé : Équation diophantienne ax+by = c

Claude-Gaspard Bachet de Méziriac a compris la relation entre les fractions continues et l'équation diophantienne linéaire.

L'équation diophantienne linéaire est l'équation suivante, où a, b et c sont des nombres entiers et où les solutions recherchées sont formées d'un couple d'entiers :

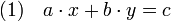
$(1)\quad a\cdot x + b \cdot y = c\;$

L'identité de Bézout indique que, si c est un multiple du plus grand commun diviseur de a et b, il existe toujours une solution. La fraction continue offre une méthode effective pour trouver toutes les solutions. Illustrons là par l'exemple 1245.x + 279.y = 6. Le développement en fraction continue de 1245/279 est égal à [4,2,6,7]. Calculons les différentes réduites, on trouve 4, 9/2, 58/13 puis 415/93. L'algorithme s'arrête, ce qui signifie que 415/93 est égal à 1245/279. En utilisant les coefficients de l'avant dernière réduite, on remarque que :

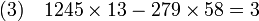
$(3)\quad 1245\times 13 - 279 \times 58 = 3$

Dans cet exemple, 3 est le plus grand commun diviseur entre 1245 et 279. Ce résultat n'est pas le fruit du hasard, l'avant dernière réduite est toujours composée d'un couple solution de l'équation de Bézout et le résultat du dernier calcul est nécessairement le plus grand commun diviseur au signe près. En effet, notons h_j et k_j la j^ième réduite de la fraction a / b. Si n est l'indice de la dernière réduite, alors a / b est égal à h_n / k_n. Une des premières propriétés assure que :

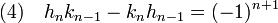
$(4)\quad h_nk_{n-1} - k_nh_{n-1} = (-1)^{n+1}\;$

On en déduit qu'un diviseur commun à h_n et k_n divise le terme de gauche et donc le terme de droite de l'égalité (4), comme les seuls diviseurs de ±1 sont ±1, les deux termes h_n et k_n sont premiers entre eux. On en déduit que a = p.h_n et b = p.k_n et :

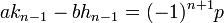
$ak_{n-1} - bh_{n-1} = (-1)^{n+1}p\;$

Cette solution démontre bien, au signe près, la propriété illustrée dans l'exemple (3). Il ne reste plus qu'à multiplier par 2 pour obtenir une solution :

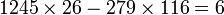
$1245\times 26 - 279 \times 116 = 6 \;$

Les autres solutions s'obtiennent par adjonction d'une solution nulle. Une solution nulle est toujours de la forme (n.93, n.415) qui s'obtiennent comme les coefficients de la dernière réduite. On obtient finalement :

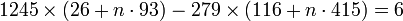
$1245\times (26 + n\cdot 93) - 279 \times (116 + n\cdot 415) = 6$

Automate planétaire

Christiaan Huygens construit un automate planétaire pour déterminer les positions relatives des corps célestes du système solaire.

Christiaan Huygens souhaite construire, à l'aide d'un mécanisme de type horlogerie un automate représentant le mouvement des planètes autour du soleil : « Ayant trouvè et fait exécuter depuis peu une machine automate qui représente les mouvements des Planètes dont la construction est d'une façon particulière et assez simple à raison de son effet, au reste d'une grande utilité à ceux qui étudient ou observent le cours des astres.^[31] ». La difficulté à laquelle il est confronté est liée au rapport de la durée d'une année terrestre et de celle de Saturne. En un an, la Terre tourne de 359° 45' 40'' 30''' et Saturne de 12° 13' 34'' 18'''. Le rapport est égal à 77 708 431/2 640 858. Combien faut-il de dents sur les deux engrenages supportant respectivement la Terre et Saturne ?

Huygens sait que les fractions continues offrent le meilleur compromis, ce qu'il exprime ainsi : « Or, lorsqu’on néglige à partir d’une fraction quelconque les derniers termes de la série et celles qui la suivent, et qu’on réduit les autres plus le nombre entier à un commun dénominateur, le rapport de ce dernier au numérateur sera voisin de celui du plus petit nombre donné au plus grand; et la différence sera si faible qu’il serait impossible d’obtenir un meilleur accord avec des nombres plus petits. »^[32].

Un calcul en fraction continue montre que :

$\frac{77\,708\,431}{2\,640\,858} = [29,2,2,1,5,1,4,1,1,2,1,6,1,10,2,2,3]\;$

On obtient la suite de fractions : 29/1, 59/2, 147/5, 206/7, 1 177/40 ... Les deux premières solutions ne sont guère précises, dans le premier cas, à la fin d'une rotation de Saturne, la position de la terre est fausse à près d'un demi-tour, dans l'autre cas l'erreur dépasse 4°. La cinquième est techniquement difficile, elle demande la fabrication d'une roue à plus de 1 000 dents ou plusieurs roues. La quatrième offre une précision proche de 3/1 000. C'est celle que choisit Huygens.

Si la terre fait cents tours complets, sur l'automate planétaire Saturne en fait 700/206, soit trois tours et un angle de 143° 18'. Dans la réalité, Saturne a tourné de 143° 26'. Soit une erreur de 8 minutes d'angle, largement inférieure aux imprécisions mécaniques de l'horloge. Un calcul analogue montre que la fraction 147/5 donne, dans le même contexte, une erreur supérieure à un degré, pour une mise en œuvre d'une difficulté technique comparable.

Fraction continue généralisée

Notations

Une fraction continue généralisée est une généralisation des fractions continues où les numérateurs et dénominateurs partiels peuvent être des réels ou complexes quelconques:

$x = b_0 + \cfrac{a_1}{b_1 + \cfrac{a_2}{b_2 + \cfrac{a_3}{b_3 + \cfrac{a_4}{\ddots\,}}}}$

où a_n (n > 0) sont les numérateurs partiels et les b_n les dénominateurs partiels, en particulier le coefficient b₀ est appelé la partie entière de la fraction.

Des notations plus compactes sont employées:

$x = b_0+ \frac{a_1}{b_1+}\, \frac{a_2}{b_2+}\, \frac{a_3}{b_3+}\cdots$

Alfred Pringsheim les écrivaient comme suit:

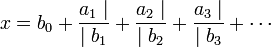$x = b_0 + \frac{a_1 \mid}{\mid b_1} + \frac{a_2 \mid}{\mid b_2} + \frac{a_3 \mid}{\mid b_3}+\cdots\,$ .

Karl Friedrich Gauss utilisa une notation rappelant la notation Σ des séries ou Π du produit infini:

$x = b_0 + \underset{i=1}{\overset{\infty}{K}} \frac{a_i}{b_i}.\,$

où la lettre K est l'initiale de Kettenbrüche, signifiant "fraction continue" en allemand. Cette notation suggère cependant des simplifications de diviseurs communs aux numérateurs et dénominateurs partiels, qui modifient la fraction continue.

Equation du second degré

L'Algebra de Raphaël Bombelli contient la première fraction continue connue en Europe, elle correspond à celle donné en exemple dans ce paragraphe.

Un exemple d'illustration de l'arrivée naturelle d'une fraction continue généralisée est l'équation du second degré. Étudions le cas particulier, correspondant celle de Bombelli^[33], la première connue en Europe :

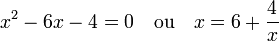
$x^2 -6x - 4 = 0 \quad\text{ou}\quad x = 6 + \frac 4x \;$

En remplaçant x par sa valeur, on obtient, comme valeur de x :

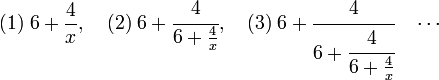
$(1)\; 6 + \frac 4x,\quad (2)\; 6 + \cfrac 4{6 + \frac 4x},\quad (3)\;6 + \cfrac 4{6 + \cfrac 4{6 + \frac 4x}} \quad\cdots$

En notation de Pringsheim, la fraction f prend la forme suivante :

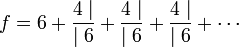
$f = 6 + \frac{4\mid}{\mid 6} + \frac{4 \mid}{\mid 6} + \frac{4 \mid}{\mid 6} +\cdots$

Cette fois ci, aucun théorème n'indique la convergence a priori d'une fraction continue de cette nature. Un calcul manuel montre que les premières réduites sont 2, 9/2, 28/9, 101/8, 342/101. On vérifie bien que cette suite tend vers une des deux racines, ici celle égale à 3 + √13. D'une manière générale, si l'équation admet au moins une racine réelle et si le coefficient de x dans l'équation du second degré n'est pas nul, cette fraction continue généralisée tend vers la racine de plus grande valeur absolue. En revanche, dans les autres cas, la fraction continue n'est pas convergente, ainsi aucun théorème ne peut garantir la convergence d'une fraction continue quelconque. Ce résultat est l'œuvre d'Euler^[22]. À l'époque de Bombelli, l'intérêt principal de cette fraction continue était d'offrir une méthode d'extraction de racine, le calcul de la fraction permet d'approcher √13 avec toute la précision souhaitée.

Démonstration

Étudions le cas général de l'équation du second degré :

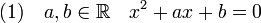
$(1)\quad a,b\in \mathbb R \quad x^2 +ax +b = 0 \;$

Si le cas semble ne pas tout à fait être général car le coefficient dominant, celui de x² est égal à 1, il est possible de remarquer qu'en divisant par ce coefficient l'équation du second degré, on revient à la situation étudiée.

La méthode proposée ici est générale pour l'étude de la convergence d'une fraction continue généralisée. Les relations de récurrences deviennent, si on ajoute un indice -1 :

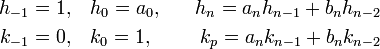
$\begin{align} h_{-1} = 1,\quad & h_0 = a_0,\quad & h_n = a_nh_{n-1}+b_nh_{n-2} \\ k_{-1} = 0,\quad & k_0 = 1,\quad & k_p = a_nk_{n-1}+b_nk_{n-2}\end{align}$

Ici (a_n) désigne la suite des coefficients des dénominateurs, correspondant au cas de la fraction continue simple et (b_n) à celle des coefficients des numérateurs, égaux à 1 dans le cas d'un fraction simple.

Il devient possible d'écrire les relations de récurrence de manière matricielle. Si H_n désigne la matrice colonne de coordonnées h_n et h_n-1 et K_n son équivalent pour le dénominateur, la relation de récurrence s'écrit aussi :

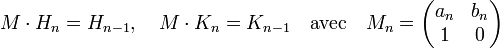
$M\cdot H_n = H_{n-1},\quad M\cdot K_n = K_{n-1}\quad\text{avec}\quad M_n = \begin{pmatrix} a_n & b_n \\ 1 & 0 \end{pmatrix}$

La question, dans le cas général, revient à une multiplication de matrice 2x2. Si N_n désigne la matrice produit des M_j pour j plus petit ou égal à n, on obtient :

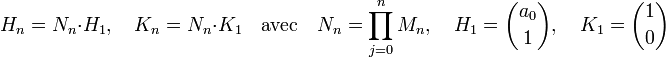
$H_n = N_n\cdot H_1,\quad K_n = N_n\cdot K_1\quad\text{avec}\quad N_n = \prod_{j=0}^n M_n,\quad H_1 = \binom{a_0}{1},\quad K_1 = \binom 10$

Pour le cas particulier de l'équation qui nous intéresse, le problème n'est pas si complexe car a_n est égal à -a et b_n à -b, et on remarque que k_n est égal à h_n-1. La matrice M_n est ainsi indépendante de n et la résolution de la question revient à calculer les puissances d'une matrice 2x2. Une autre manière de voir les choses est de remarquer que la relation de récurrence est linéaire et d'appliquer directement les résultats. L'objectif de la suite de la démonstration est l'illustration d'un cas simple d'un produit de n matrices 2x2, configuration fréquente dans le cas de l'étude d'une fraction continue.

La méthode la plus simple de résolution est, si possible, de diagonaliser M, ce qui revient à écrire que M est égal à P.D.P ^-1 où D désigne une matrice diagonale et P une matrice de passage. La matrice N_n est égale à P.D ⁿ.P ^-1. Pour cela, il est nécessaire de trouver les valeurs propres δ₁ et δ₂ de la matrice M, qui correspondent aux racines du polynôme caractéristique, qui se trouve être celui de l'équation (1). Deux cas se présentent :

Les racines de l'équation (1) sont distinctes (complexes ou réelles) :

Si les valeurs propres sont distinctes, il existe deux vecteurs propres libres, qui forment une base. La matrice Dⁿ est diagonale de valeurs propres δ₁ⁿ et δ₂ⁿ. L'expression de h_n est nécessairement une combinaison linéaire des deux valeurs propres de la matrice Dⁿ, ce qui montre l'existence de deux coefficients non nuls λ et μ tel que :

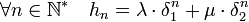
$\forall n \in \mathbb N^* \quad h_n = \lambda\cdot \delta_1^n + \mu\cdot \delta_2^n$

Les deux coefficients ne peuvent être nuls, pour s'en rendre compte, il suffit de remarquer que K₁ n'est pas un vecteur propre, on en déduit que K_n-1 et K_n ne le sont pas non plus, or si l'un des coefficients était nul les deux vecteurs colonnes K_n-1 et K_n sertaient proportionnels, ce qui ne peut arriver que dans le cas d'un vecteur propre. Pour calculer la n^e réduite, il suffit de remarquer que k_n est égal à h_n-1. On désigne par δ₁ la plus grande des deux racines en valeur absolue si elles sont réelles et en module, si elles sont imaginaires. Si a et b ne sont pas tous les deux nuls (le cas a et b tous deux nuls n'a pas d'intérêt ici), δ₁ est nécessairement différent de 0, car les racines sont supposées distinctes et ne peuvent être toutes les deux nulles, ce qui permet d'écrire :

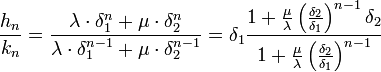
$\frac {h_n}{k_n} = \frac {\lambda\cdot \delta_1^n + \mu\cdot \delta_2^n}{\lambda\cdot \delta_1^{n-1} + \mu\cdot \delta_2^{n-1}} = \delta_1 \frac{1 + \frac{\mu}{\lambda}\left(\frac{\delta_2}{\delta_1}\right)^{n-1}\delta_2}{1 + \frac{\mu}{\lambda}\left(\frac{\delta_2}{\delta_1}\right)^{n-1}}$

Ce cas se divise alors en deux :

Le coefficient b n'est pas nul et les racines sont réelles :

Dans ce cas, δ₁ est en valeur absolue strictement supérieur à δ₂ et leur quotient à la puissance n - 1 tend vers 0, la réduite d'indice n converge vers δ₁.

Le coefficient b est nul ou les racines sont imaginaires :

Si b est nul δ₁ et δ₂ sont de signes opposés, si les racines sont imaginaires elles sont conjuguées et de même module leur rapport est dans les deux cas une valeur ω qui est un nombre complexe de module 1. La valeur ω^n-1 tourne dans le cercle unité et ne converge pas, La réduite d'indice n n'est donc pas convergente.

Les racines de l'équation (1) sont doubles :

Notons δ la racine. Une diagonalisation est impossible, mais la réduction de Jordan montre que la matrice est somme d'une matrice d'homothétie H de rapport δ et d'une matrice nilpotente R constituée uniquement de 0 sauf pour le coefficient en haut à droite, égal à 1. Comme la matrice H est celle d'une homothétie, elle commute avec R et il est possible d'appliquer la formule du binôme, ce qui donne, en remarquant que toutes les puissances R^j sont nuls si j > 1 :

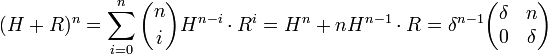
$(H + R)^n = \sum_{i=0}^{n} \binom ni H^{n-i}\cdot R^i = H^n + nH^{n-1}\cdot R = \delta^{n-1} \begin{pmatrix} \delta & n \\ 0 & \delta \end{pmatrix}$

On en déduit encore l'existence de deux coefficients λ et μ tel que :

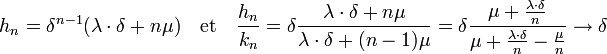
$h_n = \delta^{n-1}(\lambda\cdot\delta + n\mu)\quad\text{et}\quad \frac {h_n}{k_n} = \delta \frac{\lambda\cdot\delta + n\mu}{\lambda\cdot\delta + (n-1)\mu} =\delta \frac{\mu + \frac {\lambda\cdot\delta}n}{\mu + \frac {\lambda\cdot\delta}n - \frac{\mu}n} \rightarrow \delta$

Et, si n croît indéfiniment, la fraction réduite d'indice n tend vers l'unique racine.

Fraction continue de π et de e

Article détaillé : Approximant de Padé.

Leonhard Euler calcule le premier approximant de Padé.

Un calcul, dans la partie introductive de l'article, montre comment déterminer la fraction continue de π. Néanmoins, chaque étape est plus pénible car elle demande une précision sur la valeur initiale de plus en plus grande. Les séries entières, convergeant vers π, offrent bien une solution théorique pour le calcul de chaque coefficient de la fraction continue, mais il est calculatoirement trop inextricable pour être utilisable. Pour cette raison, il est plus simple d'obtenir une expression en fraction continue généralisée. La suivante est l'œuvre de Brouncker^[34] :

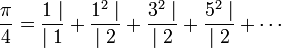
$\frac {\pi}4 = \frac{1 \mid}{\mid 1} + \frac{1^2 \mid}{\mid 2} + \frac{3^2 \mid}{\mid 2} + \frac{5^2 \mid}{\mid 2} + \cdots$

La démonstration se trouve dans l'article Fraction continue et approximation diophantienne.

Pour obtenir celle de e, on utilise un développement en fraction continue, non pas d'un nombre mais d'une fonction, plus précisément celle de l'exponentielle :

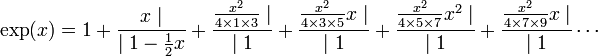
$\exp(x) = 1 + \frac{x\mid}{\mid 1-\frac 12x} + \frac{\frac {x^2}{4\times 1 \times 3} \mid}{\mid 1} + \frac{\frac {x^2}{4\times 3\times 5}x \mid}{\mid 1} + \frac{\frac {x^2}{4\times 5\times 7}x^2 \mid}{\mid 1} + \frac{\frac {x^2}{4\times 7\times 9}x \mid}{\mid 1}\cdots$

Sa construction se trouve dans l'article Approximant de Padé de la fonction exponentielle. Ainsi, une fraction continue ne s'applique pas uniquement aux nombres, mais aussi à certaines fonctions. Le développement de π/4 présentée ici, peut être vu comme une fraction continue d'approximants de Padé de la série entière de la fonction Arctangente.

Voir aussi

Notes

↑ Pour Jean Dieudonné, « le terme traditionnel en français est « fraction continue », ce qui risque d'entraîner des confusions fâcheuses lorsque la fraction dépend d'un paramètre variable ; l'anglais évite cette confusion en disant continued et non continuous » (Jean Dieudonné (dir.), Abrégé d'histoire des mathématiques 1700-1900 [détail des éditions] ), d'où la traduction littérale de « fraction continuée ».
↑ L'association à l'algorithme d'Euclide est traité dans cet article, celui avec les fonctions méromorphes se trouve, par exemple dans l'article qui valu à Henri Padé le Grand prix de l'Académie des sciences de Paris en 1906 Recherches sur la convergence des développements en fractions continues d'une certaine catégorie de fonction Annales scientifique que l'E.N.S 3^ième série tome 24 1907 p 341-400 Lire en Pdf
↑ M. Couchouron Développement d'un réel en fractions continues Un texte pour la préparation à l'agrégation de mathématiques de l'Université de Rennes I
↑ La résolution historique est l'œuvre de : J. L. Lagrange Solution d'un Problème d'arithmétique dont la publication originale se trouve dans L. Euler et J. L. Lagrange Éléments d'algèbre Lyon, Bruyset et Paris, Desaint 1774
↑ J. Liouville Communication verbale, Compte rendu des séances de l'Académie des Sciences 13 mai 1844 lire
↑ L. Euler De fractionibus continuis dissertation 1737. Une analyse historique est proposée par : A. Sandifer How Euler did it M.A.A. on line 2006
↑ La transcendance de e est l’œuvre de C. Hermite Sur la fonction exponentielle Compte rendu de l'Académie des sciences p 18 (1873) lire sur Gallica, celle de π est démontrée dans : F. Lindemann Über die Zahl π Mathematische Annalen 20 (1882) pp. 213–225.
↑ Un exemple introductif est fourni par l'auteur de la théorie : H. Padé Mémoire sur les développements en fractions continues de la fonction exponentielle Annales scientifiques de l'École normale supérieure Sér. 3 p 395 (1899) Lire en Pdf
↑ Une étude de la convergence de telles fractions continues est par exemple celle de : T. J. Stieltjes Recherches sur les fractions continues Annales de la faculté des sciences de Toulouse 1894 Lire sur Gallica
↑ Une référence sur cette question est : A. Khintchine Continued fractions Dover Publications 1997 (ISBN 0486696308)
↑ F. Engel Entwicklung der Zahlen nach Stammbruechen Verhandlungen der 52. Versammlung deutscher Philologen und Schulmaenner in Marburg, pp. 190–191 1913
↑ G Ifrah Histoire universelle des chiffres: L'intelligence des hommes racontée par les nombres et le calcul Robert Laffont 1994 (ISBN 2221901002)
↑ J. Stillwell Mathematics and its History Springer Science 2^ième éd 2004 p 72-74 (ISBN 0387953361)
↑ Bhāskara II Bijaganita 1150 cf le site de l'Université de St Andrew Pell's equation
↑ M. T. Rivolo A. Simi The computation of square and cube roots in Italy from Fibonacci to Bombelli (Italian) Arch. Hist. Exact Sci. 52 (2) 1998 pp 161-193
↑ S. Maracchia Estrazione di radice quadrata secondo Cataldi Archimede 28 (2) 1976 pp 124-127
↑ L. Hua J. Rousseau Fermat a-t-il démontré son grand théorème? l'hypothèse "Pascal" L'Harmattan 2002 p 113 (ISBN 2747528367)
↑ John Wallis un mathématicien anglais rétorqua : il ne trouvera pas mauvais, je crois, que nous lui rendions la pareille, et cela, non pas sur une bagatelle. Ces informations sont extraites du site : Pierre de Fermat par la ville Beaumont de Lomagne
↑ J. Dutka Wallis's product, Brouncker's continued fraction, and Leibniz's series Arch. Hist. Exact Sci. 26 (2) 1982 pp 115-126
↑ John Wallis Arithmetica infinitorum (traduction l'arithmétique des infinitésimaux) 1655
↑ Ces informations, comme l'essentiel de ce paragraphe proviennent de l'article : C. Brezinski Ces étranges fractions qui n’en finissent pas Lire Université des Sciences et Technologies de Lille France p 50
↑ ^{a et b} Leonhard Euler, Introductio in analysin infinitorum. Vol. I, Chapter 18 1748
↑ Ces résultats sont publiés dans : Leonhard Euler et Joseph-Louis Lagrange Eléments d'algèbre Lyon, Bruyset et Paris, Desaint 1774. Le livre contient une centaine de pages nommées Additions par Lagrange. Elles contiennent les deux preuves citées.
↑ Evariste Galois annonce le résultat suivant « Si une des racines d’une équation de degré quelconque est une fraction immédiatement périodique, cette équation aura nécessairement une autre racine également périodique que l’on obtiendra en divisant l’unité négative par cette même fraction continue périodique écrite dans un ordre inverse. » extrait de : Histoire de fractions continues par C. Bresinski de l'université des Sciences et Technologies de Lille p 63
↑ C. Hermite Sur la fonction exponentielle Compte rendu de l'Académie des sciences p 18 (1873) lire sur Gallica
↑ H. Padé Sur la représentation approchée d'une fonction par des fractions rationnelles Thèse de Doctorat présentée à l'Université de la Sorbonne 1892
↑ Voir par exemple H. Poincaré méthodes nouvelles de la mécanique céleste 3 vol Gauthier-Villars Paris 1892-1899
↑ J. F. Fleuron A Note on the History of the Cantor Set and Cantor Function Mathematics Magazine, Vol. 67 N° 2 pp 136-140 1994
↑ M. R. Schroeder Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise W.H.Freeman & Co Ltd 1991 (ISBN 0716721368)
↑ ^{a et b} Ces démonstrations proviennent du site Développement d'un réel en fractions continues par M. Couchouron pour les développements périodiques et l'équation de Pell-Fermat
↑ C. Huygens Pensees meslees § 24 1686
↑ Cette citation est extraite de : C. Brezinski Ces étranges fractions qui n’en finissent pas Université des Sciences et Technologies de Lille France p 51 Lire
↑ R. Bombelli L'algèbre 1579 Lire
↑ J. Wallis Arithmetica Infinitorum 1656

Liens externes

(en) Un calculateur en ligne de fraction continue
(fr) Développement d'un réel en fractions continues par M. Couchouron pour les développements périodiques et l'équation de Pell-Fermat
(fr) Une démonstration pour la meilleure approximation par N. Brisebarre de l'Université de Saint-Étienne
(fr) Histoire de fractions continues par C. Bresinski de l'Université des Sciences et Technologies de Lille
(fr) Joseph-Louis Lagrange Addition aux éléments d'Algèbre d'Euler : Un texte introduction d'une centaine de pages résumant l'essentiel du savoir sur les fractions continue à la fin du XVIII^e siècle.
(de) Une illustration graphique de l'algorithme d'Euclide itéré pour le calcul d'une fraction continue (avec Cinderella).

Bibliographie

Roger Descombes, Éléments de théorie des nombres, Puf Mathématiques, 1986
Le Petit Archimède, Numéro spécial π
Jean-Paul Delahaye, Le fascinant nombre π, Pour La Science, Belin, 1997 (ISBN 2-9029-1825-9)
Jean Dieudonné (dir.), Abrégé d'histoire des mathématiques 1700-1900 [détail des éditions]

Marc Guinot, Arithmétique pour amateurs. Vol. 4 : Lagrange et Legendre Aléas, 1996 (ISBN 2-908016-71-0)
Alain Faisant, L'équation diophantienne du second degré, Hermann, 1991
(en) G. H. Hardy et E. M. Wright An Introduction to the Theory of Numbers [détail des éditions]
(en) A. I. Khintchine, Continued Fractions, University of Chicago Press.
Jean Trignan, Fractions continues & Différences finies, Éditions du Choix, 1994 (ISBN 2-909028-16-X)
Bulletin de l'APMEP n° 450

Portail des mathématiques

La version du 15 août 2008 de cet article a été reconnue comme « bon article » (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu.

Ce document provient de « Fraction continue ».

Catégories : Bon article | Fraction continue | Analyse réelle | Fraction

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fractions continuées de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

DIOPHANTIENNES (APPROXIMATIONS) — La théorie des approximations diophantiennes concerne principalement l’approximation des irrationnels par des rationnels. Dans le cas d’un seul irrationnel, un rôle essentiel est joué par les fractions continuées (utilisées dès 1650 par Huygens… … Encyclopédie Universelle
LAGRANGE (J. L.) — Au crépuscule du XVIIIe siècle, le mathématicien Lagrange a donné au calcul des variations sa formulation générale en l’abordant de manière purement analytique; il appliquera ses méthodes à la mécanique dont il donne un exposé systématique qui… … Encyclopédie Universelle
Methode chakravala — Méthode chakravala Aryabhata s intéresse à l arithmétique. Il établit les fondements de la méthode chakravala. En mathématiques et plus précisément en arithmétique, la méthode chakravala est un algorithme pour résoudre les équations… … Wikipédia en Français
Méthode Chakravala — Aryabhata s intéresse à l arithmétique. Il établit les fondements de la méthode chakravala. En mathématiques et plus précisément en arithmétique, la méthode chakravala est un algorithme pour résoudre les équations diophantiennes équivalentes à… … Wikipédia en Français
Méthode chakravala — Âryabhata s intéresse à l arithmétique. Il établit les fondements de la méthode chakravala. En mathématiques et plus précisément en arithmétique, la méthode chakravala est un algorithme pour résoudre les équations diophantiennes équivalentes à… … Wikipédia en Français
HERMITE (C.) — Les travaux du mathématicien français Charles Hermite portent surtout sur l’algèbre, la théorie des nombres et l’analyse. On lui doit de très nombreux résultats sur la théorie des invariants et sur les fonctions elliptiques et abéliennes, et il… … Encyclopédie Universelle
NOMBRES (THÉORIE DES) — DANS la plupart des civilisations parvenues au stade de l’écriture, les nombres entiers ont, dès l’origine, été liés à des pratiques religieuses ou magiques, et leurs propriétés ont exercé une sorte de fascination sur les esprits, qui est loin… … Encyclopédie Universelle
Diophantienne — Équation diophantienne Édition de 1670 des Arithmétiques de Diophante d Alexandrie. Une équation diophantienne, en mathématiques, est une équation dont les coefficients sont des nombres entiers et dont les solutions recherchées sont également… … Wikipédia en Français
Equation diophantienne — Équation diophantienne Édition de 1670 des Arithmétiques de Diophante d Alexandrie. Une équation diophantienne, en mathématiques, est une équation dont les coefficients sont des nombres entiers et dont les solutions recherchées sont également… … Wikipédia en Français
Philippe Flajolet — Philippe Flajolet, en 2006, à la conférence Analysis of Algorithms. Philippe Flajolet (né le 1er décembre 1948 à Lyon et décédé le 22 mars 2011[1] … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fractions continuées

Fraction continue

Sommaire

Tour d'horizon

Approche intuitive

De l’algorithme d’Euclide aux fractions continues

Développement en fraction continue d'un rationnel

Développement en fraction continue du nombre π

Représentation géométrique

Repère chronologique

Approche théorique

Algorithme de développement en fraction continue pour un réel

Notations et terminologie

Réduites d'une fraction continue

Encadrement et convergence

Usages

Équation diophantienne linéaire

Automate planétaire

Fraction continue généralisée

Notations

Equation du second degré

Fraction continue de π et de e

Voir aussi

Notes

Liens externes

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Fractions continuées

Fraction continue

Sommaire

Tour d'horizon

Approche intuitive

De l’algorithme d’Euclide aux fractions continues

Développement en fraction continue d'un rationnel

Développement en fraction continue du nombre π

Représentation géométrique

Repère chronologique

Approche théorique

Algorithme de développement en fraction continue pour un réel

Notations et terminologie

Réduites d'une fraction continue

Encadrement et convergence

Usages

Équation diophantienne linéaire

Automate planétaire

Fraction continue généralisée

Notations

Equation du second degré

Fraction continue de π et de e

Voir aussi

Notes

Liens externes

Bibliographie

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link