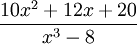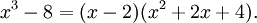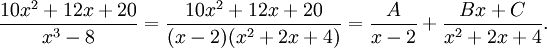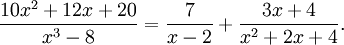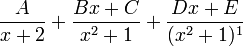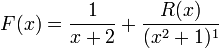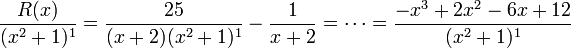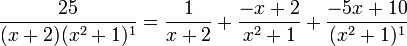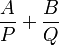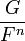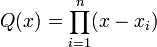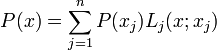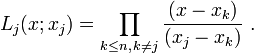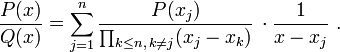- Fractions partielles
-
Décomposition en éléments simples
En algèbre, la décomposition en fractions partielles ou en éléments simples d'une fonction rationnelle est son expression sous une somme de fractions ayant pour dénominateurs des puissances de polynômes irréductibles et pour numérateurs un polynôme de degré inférieur au polynôme irréductible du dénominateur. Les fractions partielles sont utilisées dans le calcul intégral pour faciliter la recherche de primitives. Elles sont aussi utilisées pour calculer l'inverse des transformées de Laplace.
Déterminer quels polynômes sont irréductibles dépend du corps de scalaires utilisé. Ainsi, si on se limite aux nombres réels, les polynômes irréductibles auront un degré de 1 ou de 2. Si les nombres complexes sont utilisés, seuls les polynômes de premier degré seront irréductibles. De même, si on se limite aux nombres rationnels, on pourra trouver des polynômes de degré supérieurs à 2 irréductibles.
Sommaire
Mise en place
Soit P et Q deux fonctions polynomiales, on appelle fonction rationnelle, la fonction notée F dont le domaine de définition est
 et définie par
et définie par 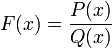 .
.On s'intéressera, dans la suite, aux fonctions rationnelles simplifiées au maximum, c'est-à-dire dans lesquelles P et Q sont premiers entre eux et où Q est de degré supérieur ou égal à 1. On notera K un corps commutatif (en général
 ou
ou  ).
).La première étape consiste à réduire la fraction de telle sorte que le degré du numérateur soit inférieur à celui du dénominateur. On procède pour ce faire à une division euclidienne de P par Q. On sait qu'il existe toujours un couple unique de polynômes T et R tels que
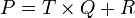 avec degré de R < degre de Q. La fonction rationnelle
avec degré de R < degre de Q. La fonction rationnelle 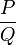 peut s'écrire alors
peut s'écrire alors 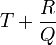 . T est appelée la partie entière de F et c'est sur
. T est appelée la partie entière de F et c'est sur 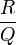 que l'on va procéder à une décomposition en éléments simples.
que l'on va procéder à une décomposition en éléments simples.Décomposition en éléments simples dans les complexes
Principes généraux
On dit que z est un pôle d’ordre p de la fraction irréductible
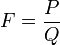 si z est un zéro (ou racine) d’ordre p de Q.
si z est un zéro (ou racine) d’ordre p de Q.Théorème — Si z est pôle d’ordre p de
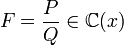 , on peut décomposer F de manière unique sous la forme
, on peut décomposer F de manière unique sous la formeoù la fraction rationnelle
 n’admet plus z comme pôle.
n’admet plus z comme pôle.Or d'après le théorème fondamental de l'algèbre, le polynôme Q possède, dans
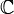 , p racines
, p racines 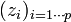 d'ordres ni avec
d'ordres ni avec 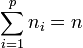 .
.La propriété précédente se généralise alors à
Théorème — Soit
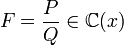 irréductible, alors si Q admet la factorisation
irréductible, alors si Q admet la factorisationalors F admet la décomposition unique en éléments simples suivante
où les
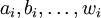 sont des nombres complexes.
sont des nombres complexes.Note: Pour des raisons de simplicité d'écriture on peut aussi noter
où les aij sont des nombres complexes.
Exemples de décompositions
L'existence d'une décomposition étant établie, la difficulté réside dans les techniques pour déterminer les différents coefficients. Ces techniques sont applicables dans le corps des complexes ou dans le corps des réels dès que le polynôme Q est produit de facteurs du premier degré. Dans un souci de lisibilité, les exemples sont ici donnés avec des coefficients réels.
Pôles de degré un
Étude d'un cas simple : Soit
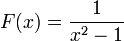
Cette fraction admet deux pôles simples 1 et -1 donc
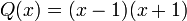 .
.On en déduit que F peut s'écrire sous la forme :
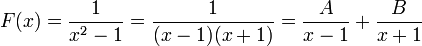
Il s'agit de déterminer A et B. Une méthode qui est toujours réalisable consiste à réduire au même dénominateur le membre de droite de la décomposition et à identifier les coefficients des numérateurs. Cette méthode n'est pas très efficace car elle demande la résolution d’un nombre d’équations correspondant au nombre de coefficients à déterminer. On peut réduire grandement le travail en éliminant, par une multiplication judicieuse, tous les coefficients sauf un. Ainsi dans notre exemple en multipliant par (x-1), on obtient
En posant alors x= 1, il vient A= 1/2
Puis, en multipliant F(x) par (x+1) et en posant x= -1, il vient B= -1/2 puisque
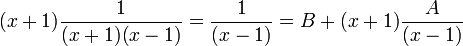
La fonction F se décompose alors en
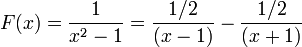
Cas plus complexe : De même, prenons la fonction rationnelle :
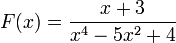 Par factorisation du polynôme bicarré et par utilisation des identités remarquables, on peut l'écrire
Par factorisation du polynôme bicarré et par utilisation des identités remarquables, on peut l'écrirequi se décompose en
Pour trouver le coefficient A, il suffit de multiplier les deux membres par x - 1 puis de remplacer x par 1
De même pour trouver B, il suffit de multiplier par x + 1 et de remplacer x par -1
Pour C, il suffit de multiplier par x - 2 et de remplacer x par 2
et pour D, on multiplie par x + 2 et on remplace x par -2
Donc
Existence d'un pôle de degré supérieur à un
Pour une fonction rationnelle de la forme
(où «
 » est un polynôme quelconque de degré strictement inférieur à 6, la décomposition en fractions partielles aura comme allure
» est un polynôme quelconque de degré strictement inférieur à 6, la décomposition en fractions partielles aura comme allureLa détermination des coefficients A, B, C, D, E, F s'opère en effectuant le changement de variable y = x + 3 (autre méthode que précédemment mais qui conduit au même résultat final). La fraction s'écrit alors
La division de P(y) par y - 1 suivant les puissances croissantes (voir Division d'un polynôme) nous donne alors
Il suffit alors d'opérer la division et de revenir à la variable de départ.
Décomposition en éléments simples dans les réels
Principes généraux
Les polynômes irréductibles à coefficients réels sont du premier ou du second degré.
Théorème — Soit
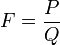 irréductible, alors si Q admet la factorisation
irréductible, alors si Q admet la factorisationoù les polynômes
 n’ont pas de racine réelle (Δ négatif) alors F admet la décomposition unique en éléments simples suivante
n’ont pas de racine réelle (Δ négatif) alors F admet la décomposition unique en éléments simples suivanteoù les aij , bgl et cgl sont des nombres réels.
Exemples de décompositions
Les méthodes de décomposition dans le cas où Q est un produit de facteurs du premier degré ont été étudiées dans la section précédente. il ne reste donc plus qu'à traiter des exemples où Q comporte un ou plusieurs facteurs irréductibles du second degré.
Existence d'un facteur irréductible du second degré
Pour décomposer
en fractions partielles, observons d'abord
Le fait que x2 + 2x + 4 ne soit pas factorisable en utilisant des coefficients réels est visible car le discriminant, 22 − 4(1)(4), est négatif. Nous cherchons donc des scalaires A, B, C tels que
Les différentes étapes sont :
- En multipliant par (x − 2) il vient :
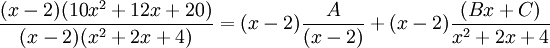
soit :
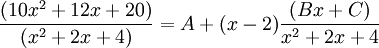
- En posant x=2 :
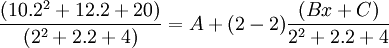
soit: 7 = A
- En posant x=0 et A=7, il vient:
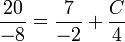
soit C=4
- En posant x=1 , A=7 et C=4 :
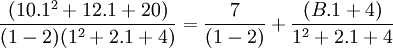
soit B=3
- La décomposition en fractions partielles est
Passage par les complexes
Une autre méthode consiste à faire la décomposition en complexe puis de regrouper deux à deux les termes à pôles conjugués et les mettre au même dénominateur pour récupérer les termes irréductibles du second degré.
On donne un exemple simple, avec P=1, Q = 1 + t3 où t est un réel:
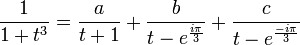
puisque − 1,
 et
et 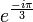 sont les racines complexes de 1 + t3. On détermine a,b,c en multipliant dans chaque cas par le dénominateur respectif puis en choisissant une valeur de t adaptée à la simplification :
sont les racines complexes de 1 + t3. On détermine a,b,c en multipliant dans chaque cas par le dénominateur respectif puis en choisissant une valeur de t adaptée à la simplification :
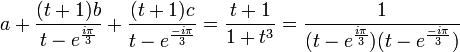
D'où, pour t = − 1 :

Par la même méthode, on trouve :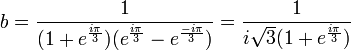 et
et
d'où
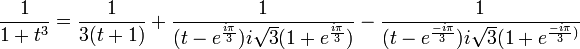
Si l'on cherche à manipuler des expressions où l'on ne rencontre que des réels, on peut alors combiner les deux derniers termes, en remarquant que b et c sont des valeurs conjuguées. Ce n'est pas un hasard puisque b et c sont des valeurs correspondant à un couple de pôles conjugués d'un polynôme à coefficients réels (c'est une propriété générale : dans une décomposition suivant les différentes racines de Q, on peut additionner les termes correspondants deux à deux).On somme alors les deux derniers termes :
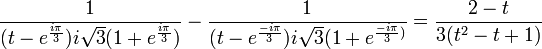
Répétition d'un facteur irréductible du second degré
avec le facteur irréductible du second degré x2 + 1 au dénominateur, la décomposition en fractions partielles sera de la forme
La détermination de A se fait en multipliant par x + 2 et en prenant x = -2. On obtient A = 1. On peut alors écrire
Ce qui donne
En remplaçant x2 + 1 par y, c'est à dire x2 par
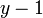
La décomposition finale est donc
Principes généraux
Existence d'une décomposition dans tout corps
Le principe de base est assez simple ; c'est plutôt le côté algorithmique qui réclamera de l'attention dans les cas particuliers.
Soit R(x) une fonction rationnelle de x qui admet une factorisation au dénominateur qu'on notera
- P(x)Q(x)
sur un corps K (par exemple les nombres réels ou les nombres complexes). Si P et Q sont premiers entre eux, alors R peut s'écrire
pour certains polynômes A(x) et B(x) sur K. L'existence d'un telle décomposition est une conséquence du fait que l'anneau des polynômes sur K est un anneau euclidien dans lequel l'égalité
- CP + DQ = 1
existe pour certains polynômes C(x) et D(x). On obtient ce dernier résultat par l'identité de Bézout.
L'utilisation de ce principe permet d'écrire R(x) comme une somme de fonctions rationnelles avec comme dénominateurs des puissances de polynômes irréductibles.
Enfin une fraction de la forme
peut s'écrire comme une somme de fractions dont le dénominateur est une puissance de F et dont les numérateurs sont de degrés inférieurs à F, plus, éventuellement un autre polynôme. Ceci peut être réalisé grâce à une succession de division euclidienne par F (la méthode est analogue à celle utilisée pour écrire un nombre en base a). Quand K est le corps des nombres complexes, F est de degré 1 (théorème fondamental de l'algèbre) et les numérateurs sont donc constants. Quand K est le corps des nombres réels, le degré de F sera 1 ou 2 et les numérateurs seront linéaires ou constants.
Cas d'un dénominateur à pôles d'ordre un
Les exemples précédents peut être généralisés à la situation suivante:
Soit Q(x) un polynôme unitaire de degré n sur un corps K dont la décomposition en facteurs de premiers degrés est
où tout les xi différents deux à deux. En d'autres mots, Q a des racines simples sur K. Si P(x) est un polynôme quelconque de degré
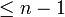 , par la formule d'interpolation de Lagrange P(x) peut être écrit de manière unique comme un somme
, par la formule d'interpolation de Lagrange P(x) peut être écrit de manière unique comme un sommeoù
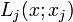 est le polynôme de Lagrange
est le polynôme de LagrangeEn divisant la représentation de Lagrange terme à terme par Q(x) dans sa forme factorisée on obtient
D'où on arrive à la décomposition en fractions partielles
Utilisations
La décomposition en éléments simples d'une fraction rationnelle a pour motivation essentielle l'intégration de la fonction rationnelle correspondante sur un intervalle de
 ne contenant aucun pôle.
ne contenant aucun pôle.En effet, on ne sait pas en général intégrer une fonction rationnelle quelconque sur un intervalle donné.
En revanche, il existe des méthodes pour intégrer les éléments simples.
Par exemple, pour intégrer la fraction rationnelle
 , il suffit de la décomposer sous la forme
, il suffit de la décomposer sous la forme 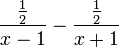 , et en intégrant directement la somme on obtient
, et en intégrant directement la somme on obtient 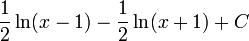
Fragments d'histoire
Voir aussi
- Portail des mathématiques
Catégorie : Polynôme
Wikimedia Foundation. 2010.

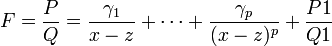
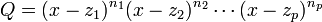
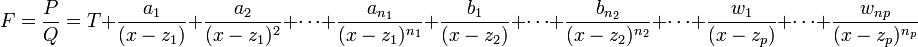
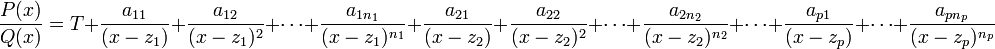
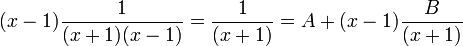

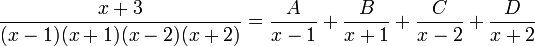
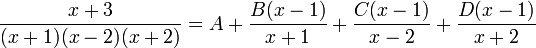
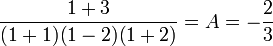
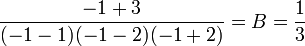
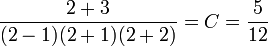
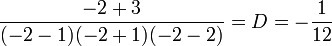
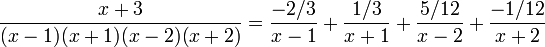
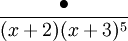

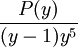
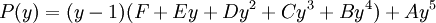

![F(x) = \begin{array}[t]{l} T+ \frac{a_{11}}{(x-z_1)}+ \frac{a_{12}}{(x-z_1)^2}+...+\frac{a_{1n_1}}{(x-z_1)^{n_1}}\\
+ \cdots\\
+ \frac{a_{p1}}{(x-z_p)}+ \frac{a_{p2}}{(x-z_p)^2}+...+\frac{a_{pn_p}}{(x-z_p)^{n_p}}\\
+ \frac{b_{11}x+c_{11}}{(x^2 - \beta_1 x + \gamma_1)}+ \frac{b_{12}x+c_{12}}{(x^2 - \beta_1 x + \gamma_1)^2} +...+ \frac{b_{1m_1}x+c_{1m_1}}{(x^2- \beta_1 x + \gamma_1)^{m_1}}\\
+...\\
+ \frac{b_{q1}x+c_{q1}}{(x^2 - \beta_q x + \gamma_q)}+ \frac{b_{q2}x+c_{q2}}{(x^2 - \beta_q x + \gamma_q)^2} +...+ \frac{b_{qm_q}x+c_{qm_q}}{(x^2- \beta_q x + \gamma_q)^{m_q}}
\end{array}](/pictures/frwiki/51/339b455937e515263dec901c0298948d.png)