Famille libre
- Famille libre
-
Famille libre

Pour les articles homonymes, voir
Famille.
En algèbre linéaire, une famille libre est une famille de vecteurs linéairement indépendants, c'est-à-dire qu'aucun des vecteurs qui la composent ne peut s'écrire comme une combinaison linéaire des autres. Une famille de vecteurs qui n'est pas libre est dite liée.
Définition mathématique
Une famille 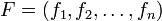 d'éléments d'un K-espace vectoriel E est dite K-libre si et seulement si :
d'éléments d'un K-espace vectoriel E est dite K-libre si et seulement si :
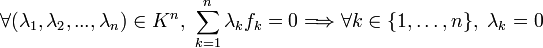
Si en plus la famille est génératrice, c'est une base de E.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Espace vectoriel
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Famille libre de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Famille Libre — Pour les articles homonymes, voir Famille. En algèbre linéaire, une famille libre est une famille de vecteurs linéairement indépendants, c est à dire qu aucun des vecteurs qui la composent ne peut s écrire comme une combinaison linéaire des… … Wikipédia en Français
libre — [ libr ] adj. • 1339; lat. liber ♦ Qui jouit de la liberté, de certaines libertés. I ♦ (Sens étroit) 1 ♦ (Opposé à esclave, serf) Qui n appartient pas à un maître. ⇒ 2. franc; affranchi. Travailleurs libres. 2 ♦ (1596) Opposé à captif, prisonnier … Encyclopédie Universelle
Famille Génératrice — En algèbre linéaire, une famille génératrice est une famille de vecteurs d un espace vectoriel dont les combinaisons linéaires permettent de construire tous les autres vecteurs de l espace. Définition Une famille d éléments d un K espace… … Wikipédia en Français
Famille generatrice — Famille génératrice En algèbre linéaire, une famille génératrice est une famille de vecteurs d un espace vectoriel dont les combinaisons linéaires permettent de construire tous les autres vecteurs de l espace. Définition Une famille d éléments d… … Wikipédia en Français
Famille (Mathématiques) — Pour les articles homonymes, voir Famille (homonymie). En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre linéaire, de la famille de… … Wikipédia en Français
Famille (mathematiques) — Famille (mathématiques) Pour les articles homonymes, voir Famille (homonymie). En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre… … Wikipédia en Français
Famille d'ensembles — Famille (mathématiques) Pour les articles homonymes, voir Famille (homonymie). En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre… … Wikipédia en Français
Famille finie — Famille (mathématiques) Pour les articles homonymes, voir Famille (homonymie). En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre… … Wikipédia en Français
Famille infinie — Famille (mathématiques) Pour les articles homonymes, voir Famille (homonymie). En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre… … Wikipédia en Français
Famille génératrice — Pour les articles homonymes, voir Génératrice. Cet article court présente un sujet plus développé dans : sous espace vectoriel engendré. En algèbre linéaire, une famille génératrice est une famille de vecteurs d un espace vectoriel dont les… … Wikipédia en Français
 Pour les articles homonymes, voir Famille.
Pour les articles homonymes, voir Famille.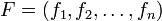 d'éléments d'un K-espace vectoriel E est dite K-libre si et seulement si :
d'éléments d'un K-espace vectoriel E est dite K-libre si et seulement si :