Famille d'ensembles

Pour les articles homonymes, voir Famille (homonymie).

En mathématiques, la notion de famille est une généralisation de celle de suite, suite finie ou suite indexée par les entiers. Ainsi on pourra parler, en algèbre linéaire, de la famille de vecteurs (u₁, u₂, … , u_n), qui est une famille finie, ou de la famille dénombrable (u_n)_{n ∈ N}. Une famille est toujours indexée, même si elle l'est parfois implicitement, par exemple dans des locutions comme « famille libre » ou « famille génératrice ».

Famille indexée : définition

Une famille 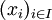indexée par un ensemble I d'éléments x_i d'un ensemble E est une application définie sur I à valeurs dans E. Il s'agit donc d'une terminologie et d'une notation, mieux adaptées à certains usages, pour la notion connue d'application (ou de fonction). Les éléments de I sont appelés indice (ou index). L'élément de la famille 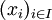d'indice i est x_i.

Quand on parle d’élément d'une famille, il s'agit d'un élément de l'ensemble image de la famille en tant qu'application : un élément de la famille 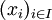est l'un quelconque des x_i.

Quand on parle de la cardinalité d'une famille, il s'agit a priori de la cardinalité de l'ensemble de ses indices (ou de façon équivalente de la cardinalité du graphe de la famille en tant qu'application). Ceci dit on peut toujours préciser : famille sur un ensemble d'indices de cardinalité telle. Ainsi une famille finie est une famille dont l'ensemble des indices est fini, une famille infinie est une famille dont l'ensemble des indices est infini, une famille dénombrable est une famille dont l'ensemble des indices est dénombrable etc. Lorsqu'une famille est finie, l'ensemble de ses éléments est fini, mais la réciproque est fausse.

On appelle également suite une famille dont l'ensemble des indices est l'ensemble des entiers ou un sous-ensemble de celui-ci, fini ou infini (les n premiers entiers, les entiers non nuls ...). Mais ce n'est pas exclusif : par exemple, en algèbre linéaire, on parle volontiers de famille de vecteurs, même dans ce cas.

Plus généralement, on pourra parler, en théorie des ensembles, de suite pour une famille dont l'ensemble des indices est un ordinal, ou même un ensemble « explicitement » bien ordonné.

Théorie axiomatique des ensembles

En théorie des ensembles une application est le plus souvent identifiée à son graphe : c'est un ensemble de couples. Une application définie sur I est un ensemble de couples tels que chaque élément de I apparait une et une seule fois en première composante d'un couple de cet ensemble. C'est donc aussi la définition de famille d'ensembles indexée par I. On se préoccupe peu de l'ensemble d'arrivée dans ce cas. On montre cependant que si {A_i}_{i ∈ I} est une famille d'ensembles, alors on peut bien parler de l’ensemble des A_i :

{A_i | i ∈ I}  « est » un ensemble.

Cela peut se démontrer en utilisant essentiellement le fait qu'une application est un ensemble de couples et le schéma d'axiomes de compréhension (il faut revenir à la définition de couple en théorie des ensembles, et utiliser l'axiome de la réunion).

Articles connexes

• Produit cartésien

• Portail des mathématiques