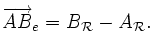Repere affine

Repere affine

Repère affine

Comme dans tout espace géométrique, un repère affine est un repère dans un espace affine qui permet d'associer de façon bi-univoque à tout point de l'espace, un ensemble de coordonnées à valeurs dans le corps sur lequel se trouve défini l'espace vectoriel associé.

Puisque les espaces affines n'ont aucune structure supplémentaire autre que la structure linéaire apportée par l'espace vectoriel, les repères affines sont aussi généraux que la structure d'espace affine le permet, et reposent sur la notion de base dans les espaces vectoriels.

Sommaire

Définition formelle

Dans un espace affine 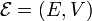\mathcal E=(E,V) de dimension n où l'espace vectoriel V porte sa structure sur le corps K, un repère affine est un couple

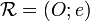\mathcal R=(O;e),

où O est un point de E (appelé origine du repère), et 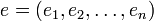e=(e_1,e_2,\dots,e_n) est une base quelconque de V.

Pour tout point M de E, les coordonnées de M dans le repère 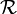\mathcal R sont tout simplement les coordonnées du vecteur 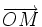\overrightarrow{OM} dans la base e de V, c'est-à-dire

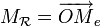M_{\mathcal R}=\overrightarrow{OM}_e,

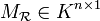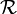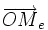où M_{\mathcal R} \in K^{n\times 1} dénote les coordonnées de M dans le repère \mathcal R, et \overrightarrow{OM}_e dénote les coordonnées du vecteur 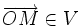\overrightarrow{OM}\in V dans la base e.

Figure 1. Repère affine dans le plan.

Cette définition est tout à fait légitime car elle est due au fait que le choix d'un point privilégié dans E permet d'établir une correspondance bijective entre l'espace des points E et l'espace vectoriel V (voir espace affine). Donc l'origine étant choisie, les coordonnées des points de E sont tout simplement les coordonnées des vecteurs associés par la correspondance bijective.

Pour tout couple de points A et B de E, l'égalité suivante découle immédiatement de la définition :

  • \overrightarrow{AB}_e=B_{\mathcal R}-A_{\mathcal R}.

Equations de changement de repère dans les espaces affines

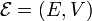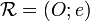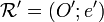Dans un même espace affine \mathcal E=(E,V) de dimension n, si \mathcal R=(O;e) et \mathcal R'=(O';e') sont deux repères différents, alors les coordonnées 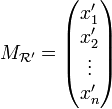M_{\mathcal R'}=\begin{pmatrix} x'_1 \\ x'_2 \\ \vdots \\ x'_n \end{pmatrix} s'obtiennent à partir des coordonnées du même point M mais dans le repère 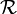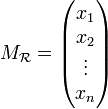\mathcal R, M_{\mathcal R}= \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} à l'aide des équations suivantes :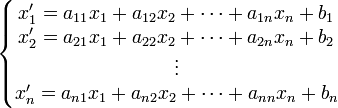

\left\{\begin{matrix} x'_1=a_{11}x_1+a_{12}x_2+\dots+a_{1n}x_n+b_1 \\ x'_2=a_{21}x_1+a_{22}x_2+\dots+a_{2n}x_n+b_2 \\ \vdots \\ x'_n=a_{n1}x_1+a_{n2}x_2+\dots+a_{nn}x_n+b_n \\ \end{matrix}\right.

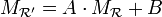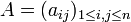qui matriciellement s'écrivent M_{\mathcal R'}=A\cdot M_{\mathcal R}+B, où A=(a_{ij})_{1\leq i,j\leq n} est la matrice de passage dans V pour passer de la base e' à la base e, et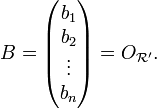 B=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}=O_{\mathcal R'}.

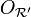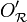La relation entre O_{\mathcal R'} et O'_{\mathcal R} est la suivante :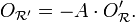

O_{\mathcal R'}=-A\cdot O'_{\mathcal R}.

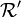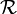Les équations de changement de repère dans l'autre sens (de \mathcal R' vers \mathcal R) s'écrivent alors :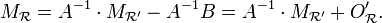

M_{\mathcal R}=A^{-1}\cdot M_{\mathcal R'}-A^{-1}B=A^{-1}\cdot M_{\mathcal R'}+O'_{\mathcal R}.

Repères affines et espace affine canonique

Tout repère affine 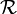\mathcal R dans un espace affine 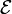\mathcal E permet d'etablir un isomorphisme (affine) entre 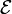\mathcal E et l'espace affine canonique An(K). En effet, l'application 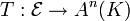T:\mathcal E\to A^n(K) définie par

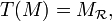T(M)=M_{\mathcal R}, pour tout point M,

c'est-à-dire l'application qui associe à tout point de 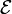\mathcal E ses coordonnées vues comme un élément de Kn, est une application affine bijective entre 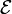\mathcal E et An(K), telle que sa réciproque est aussi affine (T est un isomorphisme affine).

Tout espace affine sur un corps K et de dimension n est alors isomorphe (se comporte de façon identique du point de vue d'un espace affine) à l'espace affine canonique An(K). Les espaces affines à étudier sont donc simplement les espaces affines canoniques (dénotés aussi An) qui servent de modèles.

Voir aussi

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Rep%C3%A8re affine ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Repere affine de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Repère affine — Comme dans tout espace géométrique, un repère affine est un repère dans un espace affine qui permet d associer de façon bi univoque à tout point de l espace, un ensemble de coordonnées à valeurs dans le corps sur lequel se trouve défini l espace… …   Wikipédia en Français

  • Repère affine cartésien — ● Repère affine cartésien (n + 1) uple formé de O (point de l espace affine A) et de n vecteurs (base de l espace vectoriel E auquel est attaché A). [O est appelé origine du repère.] …   Encyclopédie Universelle

  • affine — [ afin ] adj. • XXe; fém. de affin 1 ♦ Biol. Formes affines, présentant des ressemblances ne traduisant pas toujours des liens de parenté. Les sélaginelles sont affines aux lycopodes. 2 ♦ Math. Transformation affine : transformation dans le plan… …   Encyclopédie Universelle

  • repère — [ r(ə)pɛr ] n. m. • 1676; repaire 1578; de repaire, d apr. le lat. reperire « trouver » → répertoire 1 ♦ Marque qui sert à retrouver un emplacement, un endroit (signe, objet matériel) pour faire un travail avec précision, ajuster des pièces,… …   Encyclopédie Universelle

  • Repère direct — ● Repère direct repère affine (x0, …, xn) d un espace affine orienté, tel que est une base directe de l espace vectoriel associé …   Encyclopédie Universelle

  • Repère orthonormal — ● Repère orthonormal repère affine tel que la base qui sert à le définir est orthonormale …   Encyclopédie Universelle

  • Affine — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Affine », sur le Wiktionnaire (dictionnaire universel) Mathématiques En mathématiques, l adjectif… …   Wikipédia en Français

  • Repère cartésien — Coordonnées cartésiennes Un système de coordonnées cartésiennes permet de déterminer la position d un point sur une droite, dans un plan ou dans l espace à condition d avoir défini un repère cartésien. Il permet aussi de caractériser un vecteur.… …   Wikipédia en Français

  • Repère barycentrique — Coordonnées barycentriques En géométrie affine, les coordonnées barycentriques d un point par rapport à un repère barycentrique est une famille de poids permettant de définir ce point comme un barycentre. Sommaire 1 Définition 2 Exemple 3… …   Wikipédia en Français

  • Repère (mathématiques) — Pour les articles homonymes, voir Repère. En mathématiques, un repère est une collection d éléments de référence permettant de désigner de manière simple n importe quel objet d un ensemble donné. En géométrie, un repère permet de définir les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”