Topologie générale

Pour les articles homonymes, voir Topologie (homonymie).

un ruban de Möbius est une surface fermée dont le bord se réduit à un cercle. De tels objets sont des sujets étudiés par la topologie.

La topologie est une branche des mathématiques concernant l'étude des déformations spatiales par des transformations continues (sans arrachages ni recollement des structures).

Pour la structure formelle de topologie, voir Espace topologique.

Étymologie

Le mot « topologie » vient de la contraction des noms grecs topos et logos qui signifient respectivement « lieu » et « étude ». Littéralement, la topologie signifie l'« étude du lieu ». Elle s’intéresse donc à définir ce qu’est un lieu (appelé aussi « espace ») et quelles peuvent en être les propriétés. Une ancienne dénomination fut analysis situs, c'est-à-dire « l'étude du lieu ».

La topologie s’intéresse plus précisément aux espaces topologiques et aux applications qui les lient, dites « continues ».

Elle permet de classer ces espaces, notamment les nœuds, entre autres par leur dimension (qui peut être aussi bien nulle qu’infinie).

Elle s’intéresse aussi à leurs déformations.

En analyse, grâce aux informations qu’elle fournit sur l’espace considéré, elle permet d’obtenir un certain nombre de résultats (existence et/ou unicité de solutions d’équations différentielles, notamment).

Les espaces métriques ainsi que les espaces vectoriels normés sont des exemples d’espaces topologiques.

Idée intuitive

La topologie se distingue d'abord de la géométrie euclidienne par la conception de l'équivalence entre deux objets. En géométrie euclidienne, deux objets sont équivalents si on peut transformer l’un en l’autre à l’aide d’isométries (rotations, translations, réflexions, etc.), c'est-à-dire des transformations qui conservent la valeur des angles, des longueurs, des aires, des volumes et autres. En topologie, deux objets sont équivalents dans un sens beaucoup plus large. Ils doivent avoir le même nombre de morceaux, de trous, d’intersections etc. En topologie, il est permis de doubler, étirer, tordre etc. des objets mais toujours sans les rompre, ni séparer ce qui est uni, ni coller ce qui est séparé. Par exemple, un triangle est topologiquement équivalent à un cercle, c'est-à-dire qu’on peut transformer l’un en l’autre sans rompre et sans coller. Mais un cercle n’est pas la même chose qu’un segment (on doit casser le cercle pour obtenir le segment).

C’est la raison pour laquelle on présente parfois la topologie comme une « géométrie de la feuille de caoutchouc » : c’est comme si l'on étudiait la géométrie avec une feuille de caoutchouc que l’on pourrait contracter, étirer, etc. Une plaisanterie traditionnelle entre topologues — mathématiciens travaillant sur la topologie — raconte d'ailleurs qu’un topologue est une personne qui ne sait pas distinguer une tasse d’un beignet.

Un topologue est une personne qui ne sait pas distinguer une tasse d’un beignet.

Mais cette explication intuitive, quoique ingénieuse, est partielle et biaisée. Elle pourrait nous porter à croire que la topologie traite seulement d’objets et de concepts géométriques ; alors qu’au contraire, c’est la géométrie qui traite un certain type d’objets topologiques. Historiquement, la topologie a succédé à la géométrie, dont elle est une généralisation ; mais mathématiquement, la topologie précède la géométrie, qui n'en est qu'un cas particulier : les manuels et traités qui, comme celui de Bourbaki, procèdent du général au particulier, commencent ainsi par traiter de la topologie, dont dérivent les concepts et théorèmes de la géométrie.

Par ailleurs, il est souvent impossible de donner l’image d’une interprétation d’un problème topologique, ou de certains concepts. Tenter de visualiser les concepts est une erreur fréquente chez les débutants, qui les fait avancer très lentement quand ils ne peuvent trouver un exemple graphique. Il est fréquent d’entendre les étudiants dire qu’ils ne comprennent pas la topologie et qu’ils n’aiment pas cette branche. Généralement, on doit cette aversion au fait que le problème ne peut pas être visualisé par un dessin. Finalement, la topologie se nourrit aussi de concepts dont l’inspiration provient de l’analyse mathématique.

Histoire

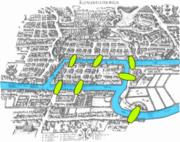Leonhard Euler, en 1736, étudia le problème des sept ponts de Königsberg. Ce fut le point de départ de la topologie moderne.

L’origine de la topologie est l’étude de la géométrie dans les cultures antiques. Le travail de Leonhard Euler datant de 1736 sur le problème des sept ponts de Königsberg est considéré comme l’un des premiers résultats de géométrie qui ne dépend d’aucune mesure, c’est-à-dire l’un des premiers résultats topologiques.

Henri Poincaré publia Analysis Situs en 1895, introduisant les concepts d'homotopie et d'homologie.

Maurice Fréchet, unifiant les travaux sur les espaces de fonctions de Cantor, Volterra, Arzelà, Hadamard, Ascoli et d’autres, introduit le concept d'espace métrique en 1906.

En 1914, Felix Hausdorff, en généralisant la notion d’espace métrique, inventa le terme d'« espace topologique » et définit ce qui s'appelle aujourd'hui l'espace séparé ou espace de Hausdorff.

Finalement, une autre légère généralisation en 1922, par Kuratowski, donna le concept actuel d'espace topologique.

Le terme « topologie », fut introduit en allemand en 1847 par Johann Benedict Listing dans Vorstudien zur Topologie.

Voir aussi

Glossaire

Articles connexes

• Heiner Zieschang
• Espace topologique
• Espace métrique
• Topologie algébrique
• Topologie faible
• Topologie de réseau
• Topologie de l'Univers

Lien externe

• Le Topologicon (une vulgarisation de la topologie en bande dessinée écrite par Jean-Pierre Petit)

• Portail des mathématiques