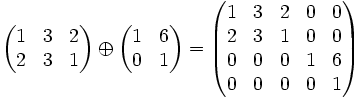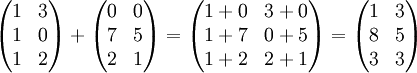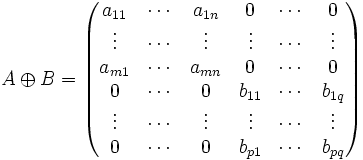Addition Matricielle
- Addition Matricielle
-
Addition matricielle
L'addition des matrices est définie pour deux matrices de même type. La somme de deux matrices de type (m, n), A = (aij) et B = (bij), notée A + B, est à nouveau une matrice (cij) de type (m, n) obtenue en additionnant les éléments correspondants, i.e.,
- pour tous i, j,
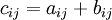
Par exemple:
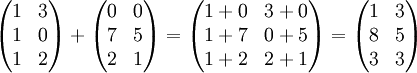
L'ensemble des matrices de type (m, n) avec la loi d'addition forment un groupe abélien.
Cette notion d'addition des matrices provient de celle des applications linéaires; si A et B sont interprétées comme des matrices d'applications linéaires relativement à des bases données, alors la matrice somme A+B représente la matrice de la somme des deux applications linéaires par rapport à ces mêmes bases.
Pour toutes matrices quelconques A (de taille m × n) et B (de taille p × q), il existe la somme directe de A et B, notée 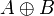 et définie par :
et définie par :
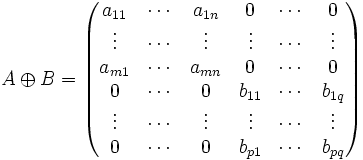
Par exemple :
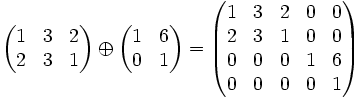
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Addition Matricielle de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Addition matricielle — L addition des matrices est définie pour deux matrices de même type. La somme de deux matrices de type (m, n), A = (aij) et B = (bij), notée A + B, est à nouveau une matrice (cij) de type (m, n) obtenue en additionnant les éléments correspondants … Wikipédia en Français
Addition des matrices — Addition matricielle L addition des matrices est définie pour deux matrices de même type. La somme de deux matrices de type (m, n), A = (aij) et B = (bij), notée A + B, est à nouveau une matrice (cij) de type (m, n) obtenue en additionnant les… … Wikipédia en Français
Fonction matricielle — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Image Matricielle — Exemple d image matricielle Une image matricielle (ou image en mode point, ou en anglais une « bitmap » ou « raster ») est une image numérique dans un format de données qui se compose d un tableau de pixels ou de points de… … Wikipédia en Français
Image matricielle — Exemple d image matricielle Une image matricielle ou image en mode point est une image numérique dans un format de données qui se compose d un tableau de pixels ou de points de couleur, généralement rectangulaire, qui peut se visualiser sur un… … Wikipédia en Français
Multiplication matricielle — Produit matriciel Le produit matriciel désigne le produit de matrices, initialement appelé la « composition des tableaux »[1]. Cet article montre comment multiplier les matrices. Sommaire 1 Produit matriciel ordinaire 1.1 Exemple … Wikipédia en Français
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Application linéaire canoniquement associée à une matrice — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Calcul matriciel — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Langage matriciel — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
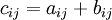
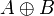 et définie par :
et définie par :